标签:ima ati cos scanf 调整 方法 ntc 函数 parallel
该问题包含以下几个子问题
CircumscribedCircle x1 y1 x2 y2 x3 y3 : 三角形外接圆
InscribedCircle x1 y1 x2 y2 x3 y3: 三角形内接圆
TangentLineThroughPoint xc yc r xp yp 过一点做圆的切线
CircleThroughAPointAndTangentToALineWithRadius xp yp x1 y1 x2 y2 r:找到半径为r,通过p点,并且与直线L相切的圆
CircleTangentToTwoLinesWithRadius x1 y1 x2 y2 x3 y3 x4 y4 r:与两条直线相切,并且半径为r
CircleTangentToTwoDisjointCirclesWithRadius x1 y1 r1 x2 y2 r2 r:求出所有与这两个圆外切,半径为r的圆
下面代码很多都是在模板基础上面写的:几何模板
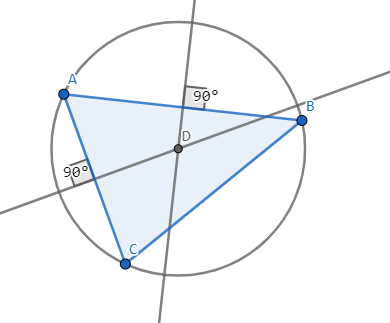
根据初中知识,三边垂直平分线的交点就是圆心,求出圆心很容易可以求出半径,所以现在需要求一个线段的垂直平分线,以及两条线段的交点。线段的中点可以用两端点取平均来求,垂直平分线可以用将向量\(\vec{AB}\) 转90度得到向量,在线段中点基础上就可以得到垂直平分线了。
// circle 结构体的构造函数
circle(Point a, Point b, Point c){
Line u = Line((a+b)/2,((a+b)/2)+((b-a).rotleft()));
Line v = Line((b+c)/2,((b+c)/2)+((c-b).rotleft()));
p = u.crosspoint(v); // p 为 u 与 v 的交点
r = p.distance(a);
}
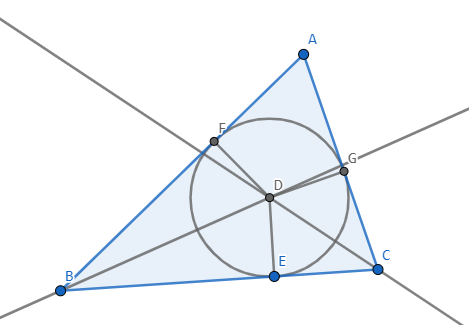
circle(Point a, Point b, Point c, bool t){
Line u, v;
// u 为角 a 的平分线, m 为ab向量极角,n为ac向量极角,取平均得到角平分线的极角
db m = atan2(b.y-a.y, b.x-a.x), n = atan2(c.y - a.y, c.x - a.x);
u.s = a;
u.e = u.s + Point(cos((n+m)/2), sin((n+m)/2)); // u.s + 角平分线单位向量得到角平分线
// v 为角 b 的平分线
m = atan2(a.y-b.y, a.x-b.x), n = atan2(c.y-b.y, c.x-b.x);
v.s = b;
v.e = v.s + Point(cos((n+m)/2), sin((n+m)/2));
p = u.crosspoint(v); // 得到圆心
r = Line(a,b).dispointtoseg(p);
}
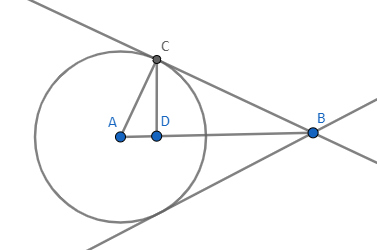
首先判断点与圆的关系
/*
点和圆的关系
0 圆外
1 圆上
2 圆内
*/
int relation(Point b){
db dst = b.distance(p);
if(sgn(dst - r) < 0) return 2;
else if(sgn(dst - r) == 0) return 1;
return 0;
}
// 过一点作圆的切线 (先判断点和圆的关系)
int tangentline(Point q, Line &u, Line &v){
int x = relation(q);
if(x == 2) return 0; //圆内
if(x == 1){ //圆上
u = Line(q, q+(q-p).rotleft());
v = u;
return 1;
}
db d = p.distance(q); // 得到AB向量的大小
db l = r * r / d; // 通过余弦定理,得到 AD向量大小
db h = sqrt(r * r - l * l); // 通过勾股定理求出DC向量大小
// vec.trunc(r) 表示将vec向量大小调整为r, rotleft表示逆时针旋转90度
u = Line(q, p + ((q - p).trunc(l) + (q - p).rotleft().trunc(h)));
v = Line(q, p + (q - p).trunc(l) + (q - p).rotright().trunc(h));
return 2;
}
先讨论 p 点与 L 的距离 dis
若\(dis \gt 2*r\) ,则没有这样的圆
若\(dis = 0\) ,则p 点在直线上,利用前面提到的方法,得到一个长度为 r 的向量,并且与直线夹角为90度,与 p 相加后可以得到圆心。(这样的圆心有两个)
其他情况可以见下图:
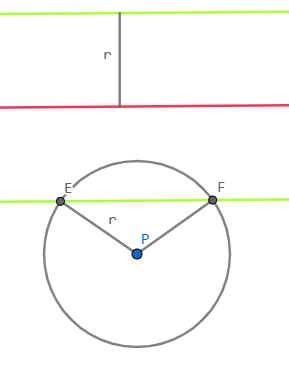
红线为L,绿线为平行线,红线与绿线的长度为 r,以 p 为圆心,r为半径做圆,与平行线交于两点(只有可能是两个点),这两点就是符合题意的圆的圆心
// 得到与直线 u 相切,过点 q, 半径为 r1 的圆
int getcircle(Line u, Point q, db r1, circle &c1, circle &c2){
db dis = u.dispointtoline(q); // 直线 u 与 q 的距离
if(sgn(dis - r1 * 2) > 0) return 0;// dis > r1 * 2
if(sgn(dis) == 0){ // q 在 u 上面
c1.p = q + ((u.e - u.s).rotleft().trunc(r1));
c2.p = q + ((u.e - u.s).rotright().trunc(r1));
c1.r = c2.r = r1;
return 2;
}
// u1, u2 为两条平行线
Line u1 = Line((u.s + (u.e - u.s).rotleft().trunc(r1)), (u.e + (u.e - u.s).rotleft().trunc(r1)));
Line u2 = Line((u.s + (u.e - u.s).rotright().trunc(r1)), (u.e + (u.e - u.s).rotright().trunc(r1)));
circle cc = circle(q, r1);
Point p1, p2;
// cc 与 u1,u2 两条线中的一个相交
if(!cc.pointcrossline(u1, p1, p2)) cc.pointcrossline(u2, p1, p2);
c1 = circle(p1, r1);
if(p1 == p2){ // 可能两个圆是重合的,这个对应 dis = 2*ri 的情况
c2 = c1;
return 1;
}
c2 = circle(p2, r1);
return 2;
}
题目保证了两条直线不是相交的,但是不妨思考一下,如果是平行的话,只有可能是 0 或者是无限个
对于不相交的情况,先上图再说(红色为l1和l2,蓝色为平行线)
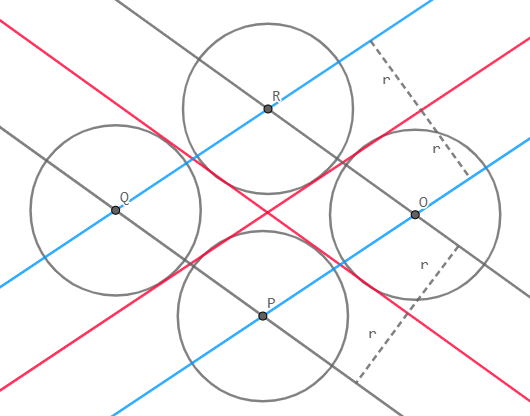
相信你一看图就明白了,就是找到两个直线的平行线求交点,这样的交点一定有四个。
// 同时与直线u,v相切,半径为r1的圆
int getcircle(Line u, Line v, db r1, circle &c1, circle &c2, circle &c3, circle &c4){
if(u.parallel(v)) return 0;
Line u1 = Line(u.s + (u.e - u.s).rotleft().trunc(r1), u.e + (u.e - u.s).rotleft().trunc(r1));
Line u2 = Line(u.s + (u.e - u.s).rotright().trunc(r1), u.e + (u.e - u.s).rotright().trunc(r1));
Line v1 = Line(v.s + (v.e - v.s).rotleft().trunc(r1), v.e + (v.e - v.s).rotleft().trunc(r1));
Line v2 = Line(v.s + (v.e - v.s).rotright().trunc(r1), v.e + (v.e - v.s).rotright().trunc(r1));
c1.r = c2.r = c3.r = c4.r = r1;
c1.p = u1.crosspoint(v1);
c2.p = u1.crosspoint(v2);
c3.p = u2.crosspoint(v1);
c4.p = u2.crosspoint(v2);
return 4;
}
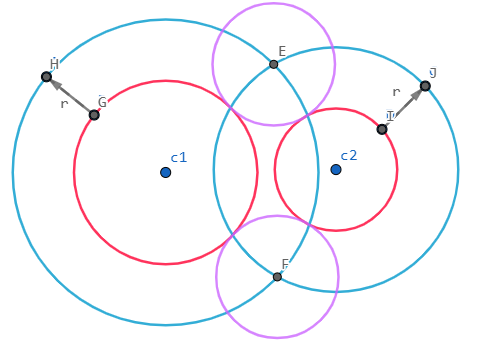
将 c1 与 c2 半径都扩大 r,求扩大的两个圆的交点即可。如何求圆的交点?
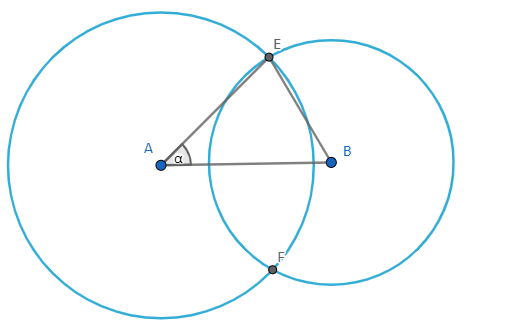
三角形\(\triangle ABE\) 三边都是确定的,由余弦定理求出\(\ang \alpha\) 的角度,然后来求出 E
/*
两圆的关系
5 相离
4 外切
3 相交
2 内切
1 内含
*/
int relationcircle(circle v){
db d = p.distance(v.p);
if(sgn(d - r - v.r) > 0) return 5;
if(sgn(d - r - v.r) == 0) return 4;
db l = fabs(r - v.r);
if(sgn(d - r - v.r) < 0 && sgn(d - l) > 0) return 3;
if(sgn(d - l) == 0) return 2;
if(sgn(d - l) < 0) return 1;
}
/*
求两个圆的交点,返回0表示没有交点,返回1是一个交点,2是两个交点
*/
int pointcrosscircle(circle v, Point &p1, Point &p2){
int rel = relationcircle(v);
// 相离或者内含
if(rel == 1 || rel == 5) return 0;
// d 为圆心距,下面求E的方法类似问题3
db d = p.distance(v.p);
db l = (d * d + r * r - v.r * v.r) / (2 * d);
db h = sqrt(r * r - l * l);
Point tmp = p + (v.p - p).trunc(l);
p1 = tmp + ((v.p - p).rotleft().trunc(h));
p2 = tmp + ((v.p - p).rotright().trunc(h));
if(rel == 2 || rel == 4)return 1;
return 2;
}
// 同时与不相交圆 cx, cy 相切,半径为r1的圆
int getcircle(circle cx, circle cy, db r1, circle &c1, circle &c2){
// 得到两个更大的圆
circle x(cx.p, r1+cx.r), y(cy.p, r1+cy.r);
// 求两个圆的交点
int t = x.pointcrosscircle(y, c1.p, c2.p);
if(!t) return 0;
c1.r = c2.r = r1;
return t;
}
AC代码
#include <cstdio>
#include <iostream>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
#define dbg(x...) do { cout << "\033[32;1m" << #x <<" -> "; err(x); } while (0)
void err() { cout << "\033[39;0m" << endl; }
template<class T, class... Ts> void err(const T& arg,const Ts&... args) { cout << arg << " "; err(args...); }
const int N = 100 + 5;
typedef double db;
const db eps = 1e-8;
const db pi = acos(-1.0);
int sgn(db x){
if(fabs(x) < eps) return 0;
if(x < 0) return -1;
return 1;
}
struct Point{
db x, y;
Point(){}
Point(db x, db y):x(x), y(y){}
void input(){
scanf("%lf%lf",&x, &y);
}
bool operator == (Point b)const {
return sgn(x-b.x) == 0 && sgn(y-b.y) == 0;
}
bool operator < (Point b)const{
return sgn(x-b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator - (const Point &b)const{
return Point(x - b.x, y - b.y);
}
db operator ^ (const Point &b)const{
return x * b.y - y * b.x;
}
db operator * (const Point &b)const{
return x * b.x + y * b.y;
}
// 返回长度
db len(){
return hypot(x, y);
}
// 返回长度平方
db len2(){
return x * x + y * y;
}
//返回两点距离
db distance(Point p){
return hypot(x - p.x, y - p.y);
}
Point operator + (const Point &b)const{
return Point(x + b.x, y + b.y);
}
Point operator * (const db &k) const {
return Point(x * k, y * k);
}
Point operator /(const db &k)const {
return Point(x / k, y / k);
}
// 逆时针旋转90度
Point rotleft(){
return Point(-y, x);
}
// 顺时针转90度
Point rotright(){
return Point(y, -x);
}
// 化为长度为 r 的向量
Point trunc(db r){
db l = len();
if(!sgn(l)) return *this;
r /= l;
return Point(x*r, y*r);
}
};
struct Line{
Point s, e;
Line(){}
Line(Point s, Point e):s(s),e(e){}
void input(){
s.input();
e.input();
}
db dispointtoline(Point p){
return fabs((p-s) ^ (e-s)) / length();
}
db length(){
return s.distance(e);
}
// 返回直线倾斜角 0 <= angle < pi
db angle(){
db k = atan2(e.y - s.y, e.x - s.x);
if(sgn(k) < 0) k += pi;
if(sgn(k - pi) == 0) k -= pi;
return k;
}
// 点到线段的距离
db dispointtoseg(Point p){
if(sgn((p-s)*(e-s)) < 0 || sgn((p-e) * (s-e)) < 0)
return min(p.distance(s), p.distance(e));
return dispointtoline(p);
}
Point crosspoint(Line v){
db a1 = (v.e - v.s) ^ (s - v.s);
db a2 = (v.e - v.s) ^ (e - v.s);
return Point((s.x * a2 - e.x * a1) / (a2 - a1), (s.y * a2 - e.y * a1) / (a2 - a1));
}
/*
返回 p 在直线上的投影
*/
Point lineprog(Point p){
return s + ( ((e-s)*((e-s)*(p-s)))/((e-s).len2()) );
}
// 两向量平行(对应直线平行或重合)
bool parallel(Line v){
return sgn((e - s) ^ (v.e - v.s)) == 0;
}
};
struct circle{
Point p;
db r;
circle(){}
circle(Point p, db r):p(p), r(r){}
bool operator < (circle b)const{
return p < b.p;
}
void input(){
p.input();
// 注意类型
scanf("%lf", &r);
}
/*
三角形的外接圆
需要Point 的 + / rotate() 以及 Line 的crosspoint()
利用两条边的中垂线得到圆心
UVA 12304
*/
circle(Point a, Point b, Point c){
Line u = Line((a+b)/2,((a+b)/2)+((b-a).rotleft()));
Line v = Line((b+c)/2,((b+c)/2)+((c-b).rotleft()));
p = u.crosspoint(v);
r = p.distance(a);
}
/*
三角形的内切圆
bool t 没有作用,只是为了和上面外接圆函数区别
UVA 12304
*/
circle(Point a, Point b, Point c, bool t){
Line u, v;
// u 为角 a 的平分线
db m = atan2(b.y-a.y, b.x-a.x), n = atan2(c.y - a.y, c.x - a.x);
u.s = a;
u.e = u.s + Point(cos((n+m)/2), sin((n+m)/2));
// v 为角 b 的平分线
m = atan2(a.y-b.y, a.x-b.x), n = atan2(c.y-b.y, c.x-b.x);
v.s = b;
v.e = v.s + Point(cos((n+m)/2), sin((n+m)/2));
p = u.crosspoint(v);
r = Line(a,b).dispointtoseg(p);
}
/*
点和圆的关系
0 圆外
1 圆上
2 圆内
*/
int relation(Point b){
db dst = b.distance(p);
if(sgn(dst - r) < 0) return 2;
else if(sgn(dst - r) == 0) return 1;
return 0;
}
/*
线段和圆的关系
比较的是圆心到线段的距离和半径的关系
2 交
1 切
0 不交
*/
int relation(Line v){
db dst = v.dispointtoseg(p);
if(sgn(dst - r) < 0) return 2;
else if(sgn(dst - r) == 0) return 1;
return 0;
}
int relationline(Line v){
db dst = v.dispointtoline(p);
if(sgn(dst - r) < 0) return 2;
else if(sgn(dst - r) == 0) return 1;
return 0;
}
// 过一点作圆的切线 (先判断点和圆的关系)
int tangentline(Point q, Line &u, Line &v){
int x = relation(q);
if(x == 2) return 0; //圆内
if(x == 1){ //圆上
u = Line(q, q+(q-p).rotleft());
v = u;
return 1;
}
db d = p.distance(q);
db l = r * r / d;
db h = sqrt(r * r - l * l);
u = Line(q, p + ((q - p).trunc(l) + (q - p).rotleft().trunc(h)));
v = Line(q, p + (q - p).trunc(l) + (q - p).rotright().trunc(h));
return 2;
}
// 求直线与圆的交点,返回交点个数
int pointcrossline(Line v, Point &p1, Point &p2){
if(!(*this).relationline(v)) return 0;
Point a = v.lineprog(p);
db d = v.dispointtoline(p);
d = sqrt(r * r - d * d);
if(sgn(d) == 0){
p1 = a;
p2 = a;
return 1;
}
p1 = a + (v.e - v.s).trunc(d);
p2 = a - (v.e - v.s).trunc(d);
return 2;
}
// 得到与直线 u 相切,过点 q, 半径为 r1 的圆
int getcircle(Line u, Point q, db r1, circle &c1, circle &c2){
db dis = u.dispointtoline(q);
if(sgn(dis - r1 * 2) > 0) return 0;
if(sgn(dis) == 0){
c1.p = q + ((u.e - u.s).rotleft().trunc(r1));
c2.p = q + ((u.e - u.s).rotright().trunc(r1));
c1.r = c2.r = r1;
return 2;
}
Line u1 = Line((u.s + (u.e - u.s).rotleft().trunc(r1)), (u.e + (u.e - u.s).rotleft().trunc(r1)));
Line u2 = Line((u.s + (u.e - u.s).rotright().trunc(r1)), (u.e + (u.e - u.s).rotright().trunc(r1)));
circle cc = circle(q, r1);
Point p1, p2;
if(!cc.pointcrossline(u1, p1, p2)) cc.pointcrossline(u2, p1, p2);
c1 = circle(p1, r1);
if(p1 == p2){
c2 = c1;
return 1;
}
c2 = circle(p2, r1);
return 2;
}
// 同时与直线u,v相切,半径为r1的圆
int getcircle(Line u, Line v, db r1, circle &c1, circle &c2, circle &c3, circle &c4){
if(u.parallel(v)) return 0;
Line u1 = Line(u.s + (u.e - u.s).rotleft().trunc(r1), u.e + (u.e - u.s).rotleft().trunc(r1));
Line u2 = Line(u.s + (u.e - u.s).rotright().trunc(r1), u.e + (u.e - u.s).rotright().trunc(r1));
Line v1 = Line(v.s + (v.e - v.s).rotleft().trunc(r1), v.e + (v.e - v.s).rotleft().trunc(r1));
Line v2 = Line(v.s + (v.e - v.s).rotright().trunc(r1), v.e + (v.e - v.s).rotright().trunc(r1));
c1.r = c2.r = c3.r = c4.r = r1;
c1.p = u1.crosspoint(v1);
c2.p = u1.crosspoint(v2);
c3.p = u2.crosspoint(v1);
c4.p = u2.crosspoint(v2);
return 4;
}
/*
两圆的关系
5 相离
4 外切
3 相交
2 内切
1 内含
*/
int relationcircle(circle v){
db d = p.distance(v.p);
if(sgn(d - r - v.r) > 0) return 5;
if(sgn(d - r - v.r) == 0) return 4;
db l = fabs(r - v.r);
if(sgn(d - r - v.r) < 0 && sgn(d - l) > 0) return 3;
if(sgn(d - l) == 0) return 2;
if(sgn(d - l) < 0) return 1;
}
/*
求两个圆的交点,返回0表示没有交点,返回1是一个交点,2是两个交点
*/
int pointcrosscircle(circle v, Point &p1, Point &p2){
int rel = relationcircle(v);
if(rel == 1 || rel == 5) return 0;
db d = p.distance(v.p);
db l = (d * d + r * r - v.r * v.r) / (2 * d);
db h = sqrt(r * r - l * l);
Point tmp = p + (v.p - p).trunc(l);
p1 = tmp + ((v.p - p).rotleft().trunc(h));
p2 = tmp + ((v.p - p).rotright().trunc(h));
if(rel == 2 || rel == 4)return 1;
return 2;
}
// 同时与不相交圆 cx, cy 相切,半径为r1的圆
int getcircle(circle cx, circle cy, db r1, circle &c1, circle &c2){
circle x(cx.p, r1+cx.r), y(cy.p, r1+cy.r);
int t = x.pointcrosscircle(y, c1.p, c2.p);
if(!t) return 0;
c1.r = c2.r = r1;
return t;
}
};
string op;
int main(){
while(cin >> op){
if(op == "CircumscribedCircle"){
Point a, b, c;
a.input();b.input();c.input();
circle C(a, b, c);
printf("(%.6f,%.6f,%.6f)\n", C.p.x, C.p.y, C.r);
}else if(op == "InscribedCircle"){
Point a, b, c;
a.input();b.input();c.input();
circle C(a, b, c, true);
printf("(%.6f,%.6f,%.6f)\n", C.p.x, C.p.y, C.r);
}else if(op == "TangentLineThroughPoint"){
Point p;
circle c;
c.input();p.input();
Line l[2];
int cnt = c.tangentline(p, l[0], l[1]);
sort(l, l+cnt, [](Line a, Line b){return a.angle() < b.angle();});
printf("[");
for(int i=0;i<cnt;i++){
if(i) printf(",");
printf("%.6f", l[i].angle()/pi*180);
}
printf("]\n");
}else if(op == "CircleThroughAPointAndTangentToALineWithRadius"){
Point p;
Line l;
db r;
p.input();l.input();scanf("%lf", &r);
circle c[2];
int cnt = circle().getcircle(l, p, r, c[0], c[1]);
sort(c,c+cnt);
printf("[");
for(int i=0;i<cnt;i++){
if(i) printf(",");
printf("(%.6f,%.6f)",c[i].p.x,c[i].p.y);
}
printf("]\n");
}else if(op == "CircleTangentToTwoLinesWithRadius"){
Line l[2];
db r;
l[0].input();l[1].input();
scanf("%lf", &r);
circle c[4];
int cnt = circle().getcircle(l[0], l[1], r, c[0], c[1], c[2], c[3]);
sort(c,c+cnt);
printf("[");
for(int i=0;i<cnt;i++){
if(i) printf(",");
printf("(%.6f,%.6f)",c[i].p.x,c[i].p.y);
}
printf("]\n");
}else if(op == "CircleTangentToTwoDisjointCirclesWithRadius"){
circle c1, c2, c[4];
c1.input();c2.input();
db r;scanf("%lf", &r);
int cnt = circle().getcircle(c1, c2, r, c[0], c[1]);
sort(c, c+cnt);
printf("[");
for(int i=0;i<cnt;i++){
if(i) printf(",");
printf("(%.6f,%.6f)",c[i].p.x,c[i].p.y);
}
printf("]\n");
}
}
return 0;
}
UVA-12304 2D Geometry 110 in 1! (有关圆的基本操作)
标签:ima ati cos scanf 调整 方法 ntc 函数 parallel
原文地址:https://www.cnblogs.com/1625--H/p/12571633.html