标签:ring 根据 就是 ios cstring 处理 http 颜色 typedef
题目链接:https://codeforces.com/problemset/problem/1327/D
根据题意,数组的第i位连第p[i]位,第p[i]位连第p[p[i]]位...一直连下去,因为存的是一个1~n的排列,所以最后一定会形成一个或多个闭环
现在我们把一个闭环单独拿出来讨论
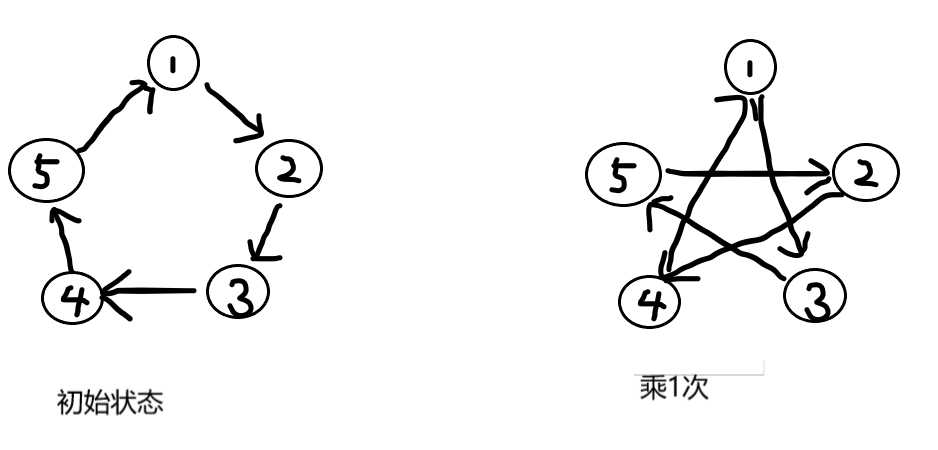
假设最初始的状态是环中节点一次连接,进行一次乘法操作后就是隔一个连接,乘两次后就是隔两个连接
乘三次就会变成1-->4-->2-->5-->3-->1,以此类推
在这其中
首先不管乘多少次此闭环中节点是绝对不会连到其他闭环的节点上去的
其次设m为闭环中节点个数,k为执行乘法操作次数,当m%(k+1)=0时原本的大闭环会变成(k+1)个小闭环,当m%(k+1)!=0时虽然连接方式有变但仍然是一整个原本的大闭环
比如m=6,当k=1时有1-->3-->5-->1,2-->4-->6-->2两个环;当k=2时有1-->4-->1,2-->5-->2,3-->6-->3三个
最后是当k+1=m时此闭环内的每个节点都会连接自己形成自环
因为我们的任务就是找到最小的k使得整个数组中存在一个闭环,环上各节点的颜色一样,由于上述第三条的存在所以答案一定存在
那么实现的方法就是对数组的每个初始的闭环进行处理,处理一个闭环时枚举k从1到m-1,当m%(k+1)==0时遍历所有产生的小闭环看是否颜色一样,复杂度大概O(n√n)吧
取所有初始闭环操作数中最小的就是答案
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
using namespace std;
typedef long long ll;
const int inf=0x3f3f3f3f;
const ll llinf=0x3f3f3f3f3f3f3f3f;
const double pi=acos(-1);
const int mod=998244353;
/****************************Link Start****************************/
int nxt[200010],col[200010];
int vis[200010];
int que[200010];
int func(int top)
{
for(int i=1;i<=top;i++) if(top%i==0)
{
for(int j=0;j<i;j++)
{
int flag=que[j];
for(int k=j;k<top;k+=i)
if(flag!=que[k]) flag=0;
if(flag) return i;
}
}
return -1;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&nxt[i]);
for(int i=0;i<n;i++) scanf("%d",&col[i]);
for(int i=0;i<n;i++) vis[i]=0;
int ans=inf;
for(int i=0;i<n;i++) if(!vis[i])
{
int t=i,top=0;
while(!vis[t])
{
que[top++]=col[t];
vis[t]=1;
t=nxt[t]-1;
}
ans=min(ans,func(top));
}
printf("%d\n",ans);
}
return 0;
}
标签:ring 根据 就是 ios cstring 处理 http 颜色 typedef
原文地址:https://www.cnblogs.com/JDZJBD/p/12576403.html