机器学习 - 命名实体识别之Hidden Markov Modelling

标签：margin   案例   帮助   turn   影响   命名   info   老王   应用   

• 概述

命名实体识别在NLP的应用中也是非常广泛的，尤其是是information extraction的领域。Named Entity Recognition(NER) 的应用中，最常用的一种算法模型是隐式马可夫模型（Hidden Markov Modelling）- HMM。本节内容主要是通过介绍HMM的原理，以及应用HMM来做一个NER的实例演示。

• HMM原理解析

在解释HMM的原理之前，先引用几个HMM的基本概念，第一个是就是隐式状态，在本文中用H表示； 第二个就是显式状态，在本文中用大写的英文字母O表示。咱们的HMM的中，就是根据咱们的显式状态O来计算隐式状态H的概率的问题，其中在HMM中有一个基本的前提条件，那就是每一个time step的隐式状态只跟它前一步的的隐式状态有关。具体是什么意思呢，大家看我下面的一幅图片,结合这幅图片来给大家解释

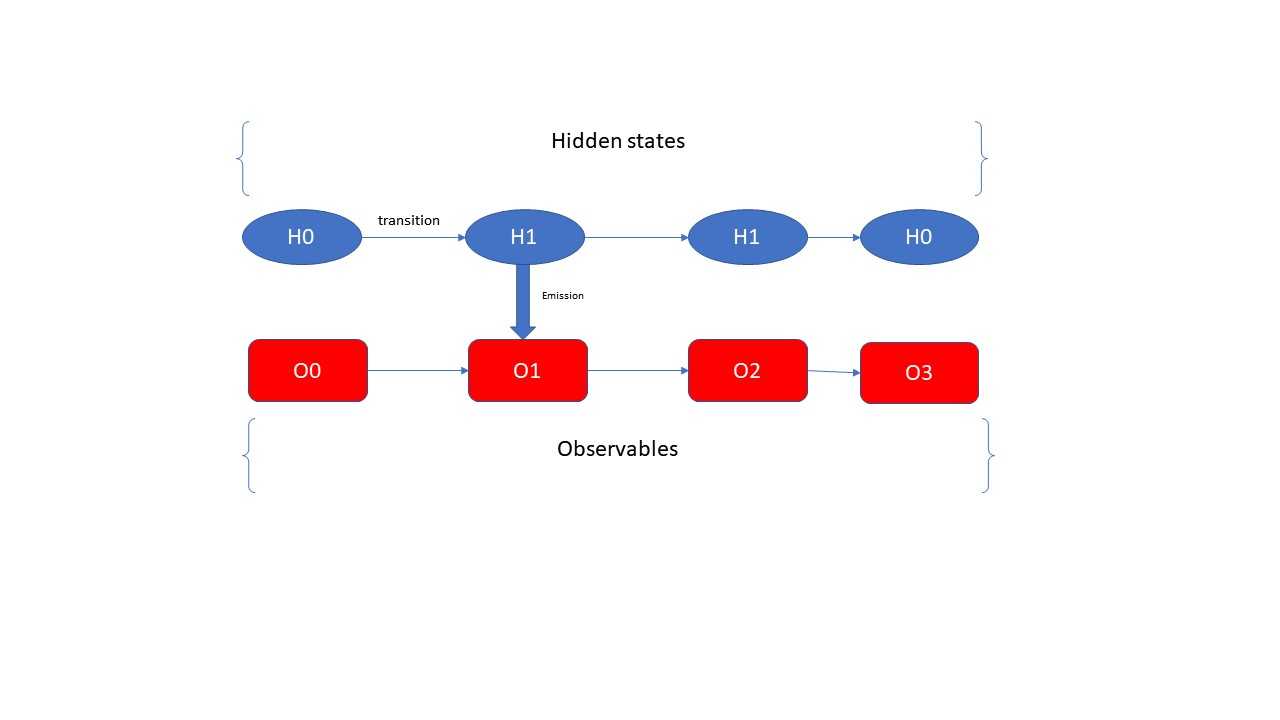
 首先observables是大家能直接得到的信息，例如一个句子“小李和王二在天津旅游”，这个就是一个observable的sequence，是咱们能够直接得到的信息；那么咱们如何才能够得到这句话背后所包含的隐式sequences呢？这就是咱们的HMM所要解决的问题了。从上图可以看出hidden states之间是通过transition matrix来连接的，这里咱们也可以很好的看出来每一步的hidden state仅仅是由前一步的hidden state来确定的；hidden state和observable之间是通过emission matrix来连接的，即在给定的hidden state的情况的，指向每一个observable的概率是多少。这么说的有点抽象，那么咱们通过下面的图片来展示这个transition matrix和emission matrix

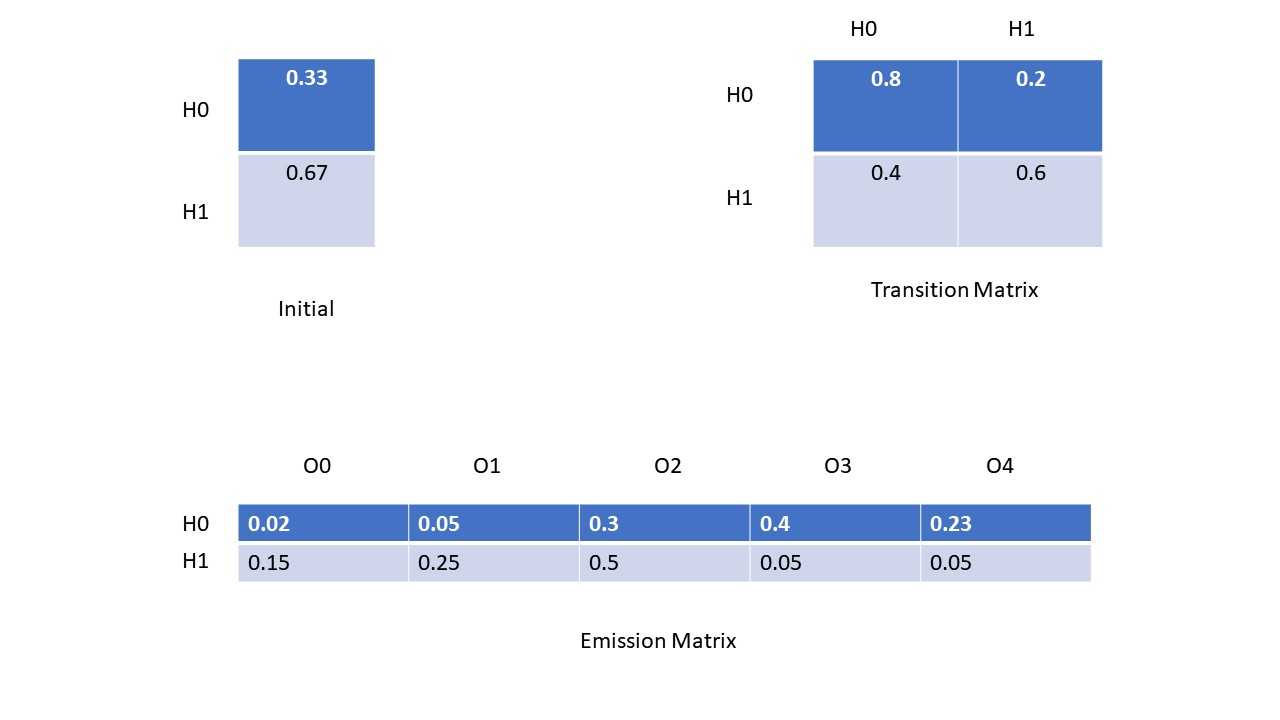
 上面的图片展示了HMM所需要的一些matrix，咱们的一个个分析。首先initial matrix是咱们根据语义集中的每一条数据的第一个hidden state计算出来的；transition matrix是根据咱们训练的语言集中的所有的隐式状态的计算出来的，例如咱们统计出所有的H0-》H0和H0-》H1的个数，然后除以总数，得出的分别就是H0-》H0和H0-》H1的概率，同理得出其他的Transition Matrix的其他的概率。Emission Matrix也是根据咱们训练的语义集中的数据计算出来的，它的步骤是统计出所有H0-》O0，O1, O2,O3,O4的个数，然后除以总数，得到的就是H0这个hidden state分别对应的所有的显式状态的概率， 同理也可以计算出其他的emission matrix的值。这就是得出Initial Matrix, Transition Matrix, 和 Emission Matrix的方法和步骤。从咱们的语义集中得出了这些数据过后，咱们就通过Vertibi算法来根据observable sequence计算了咱们的Hidden state sequences。

• Vertibi 算法

Vertibi算法是一种动态路径规划的算法，它能动态的规划处最优的路径。具体在咱们NER的应用中，它能够根据咱们的上面计算出来的Transition matrix, Initial Matrix和Emmsion Matrix来规划处咱们的最优的隐式状态的sequence， 其实这里就是寻找P（H0H1H2H3H4H5...........）最大值的一种方法，这里需要注意的一个点就是局部的最优并不一定能得出全局最优的结论，这是因为每一步的隐式状态的概率并不仅仅收到当前这一步的显式状态的影响，还受到它前一步的隐式状态的影响。下面咱们来用一个小实例来展示一下Vertibi的算法，为了方便，咱们只展示一步哈，请看下图所示

• 隐式马可夫算法和维特比算法的代码演示

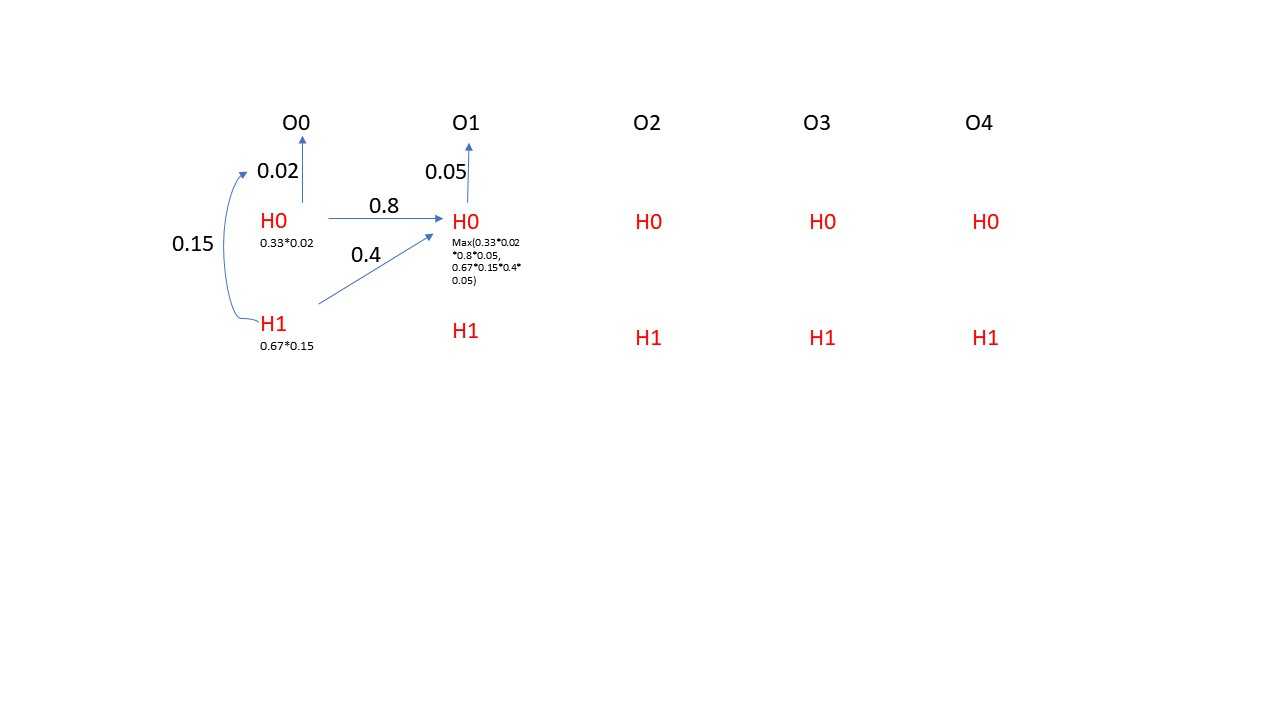
上面的部分都是分析隐式马可夫算法和维特比算法的原理，那么接下来咱们具体看看它们在NER中的应用以及实际的代码演示，这里我用一个在NLP中的实例来演示这两种算法。假设我们有一个语义集，咱们根据训练数据来计算好markov的matrix，然后应用维特比算法来抽取句子中的人名的信息出来。这在NLP中是一个非常常用的案例，那咱们首先来看看计算Initial maxtrix和Transition Matrix的代码部分

   #计算初始hidden state的概率和transition matrix
    def calculate_initial_and_transition_matrix(self):
        for dictionary in self.text_corpus:
            for i, tag in enumerate(dictionary["tags"][:-1]):
                if i == 0:
                    self.pi[self.tag_index[tag]]+=1
                current_tag = self.tag_index[tag]
                next_tag = self.tag_index[dictionary["tags"][i+1]]
                self.transition[current_tag, next_tag] += 1
        self.transition /= np.sum(self.transition, axis = 1, keepdims = True)
        self.pi /= np.sum(self.pi)
        self.pi[self.pi == 0] = 1e-8
        self.transition[self.transition == 0] = 1e-8
        return self.pi, self.transition

其次咱们来看一下计算emission matrix的代码部分

    def calculate_emmision_matrix(self):
        for dictionary in self.text_corpus:
            for word, tag in zip(dictionary["text"], dictionary["tags"]):
                self.emmision_matrix[self.tag_index[tag],self.dataloader.tokenizer.texts_to_sequences(word)[0][0]] += 1
        self.emmision_matrix /= np.sum(self.emmision_matrix, keepdims = True, axis= 1)
        self.emmision_matrix[self.emmision_matrix == 0] = 1e-8
        return self.emmision_matrix

根据咱们的训练数据咱们得出了这些matrix的值，根据这些matrix的值，咱们就可以根据输入的一句话（显式状态）来计算出这一句话中哪些字是人名（隐式状态）了，并且将这些人名信息提取出来了。这里咱们不用实际的手动的实现vertibi算法了，TensorFlow已经帮助咱们实现好了，咱们不需要再重复造轮子了，这里咱们需要引进一下TensorFlow probability这个框架了，具体的看下面的代码展示

import tensorflow_probability as tfp
import tensorflow as tf

tfd = tfp.distributions
initial_distribution = tfd.Categorical(probs=pi)
transition_maxtrix = tfd.Categorical(probs=transition)
observation_matrix = tfd.Categorical(probs = emmision)


model = tfd.HiddenMarkovModel(initial_distribution=initial_distribution,
                              transition_distribution=transition_maxtrix,
                              observation_distribution=observation_matrix,
                              num_steps=11)


test_string = "小明和老王去河边钓鱼了"
temps = [data_handler.calculator.word_index[index] for index in list(test_string)]
tag_sequence = model.posterior_mode(observations=temps)
reversed_tag_index = {value:key for key,value in data_handler.calculator.tag_index.items()}
tags = [reversed_tag_index[index] for index in tag_sequence.numpy()]
print(tags)

上面就是根据咱们的matrix(initial_distribution, transition_matrix, observation_matrix)，还有显示状态（test_string），tfp根据vertibi算法帮助咱们计算出来隐式状态的sequence（tag_sequence）。这就是NER在NLP的应用中常用的一个实例。

机器学习 - 命名实体识别之Hidden Markov Modelling

标签：margin   案例   帮助   turn   影响   命名   info   老王   应用   

原文地址：https://www.cnblogs.com/tangxiaobo199181/p/12585312.html