动态规划基本思想

标签：splay   可见   步骤   ever   include   using   时间   如何   变形   

引入

引用某OI大佬的一段话

动态规划自古以来是DALAO凌虐萌新的分水岭，但有些OIer认为并没有这么重要——会打暴力，大不了记忆化。但是其实，动态规划学得好不好，可以彰显出一个OIer的基本素养——能否富有逻辑地思考一些问题，以及更重要的——能否将数学、算筹学（决策学）、数据结构合并成一个整体并且将其合理运用qwq。我们首先要了解的，便是综合难度在所有动规题里最为简单的线性动规了。线性动规既是一切动规的基础，同时也可以广泛解决生活中的各项问题——比如在我们所在的三维世界里，四维的时间就是不可逆式线性，比如我们需要决策在相同的时间内做价值尽量大的事情，该如何决策，最优解是什么——这就引出了动态规划的真正含义：
在一个困难的嵌套决策链中，决策出最优解。

动态规划

首先，动态规划和递推有些相似（尤其是线性动规），但是不同于递推的是：
递推求出的是数据，所以只是针对数据进行操作；而动态规划求出的是最优状态，所以必然也是针对状态的操作，而状态自然可以出现在最优解中，也可以不出现——这便是决策的特性（布尔性）。其次，由于每个状态均可以由之前的状态演变形成，所以动态规划有可推导性，但同时，动态规划也有无后效性，即每个当前状态会且仅会决策出下一状态，而不直接对未来的所有状态负责，可以浅显的理解为——Future never has to do with past time ,but present does.
现在决定未来，未来与过去无关。

动态规划的定义

以下内容来自维基百科
动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。
通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

动态规划的适用情况

1.最优子结构
最优子结构性质。如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）。最优子结构性质为动态规划算法解决问题提供了重要线索。
2.无后效性
无后效性。即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响。
3.子问题重叠
子问题重叠性质。子问题重叠性质是指在用递归算法自顶向下对问题进行求解时，每次产生的子问题并不总是新问题，有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只计算一次，然后将其计算结果保存在一个表格中，当再次需要计算已经计算过的子问题时，只是在表格中简单地查看一下结果，从而获得较高的效率。

斐波那契数列

例如我们所熟知的斐波那契数列的递推式就是动态规划的一种体现

从递归搜索的角度去思考斐波那契数列

int f(int n)
{
    if(n == 1 || n == 2)return 1;
    else return f(n - 1) + f(n - 2);
}

我们会发现上面的程序在超过50项之后计算速度就会以肉眼可见的速度下降，原因是什么呢，就是因为该程序在计算的过程中遇到了大量的子问题的重叠计算。
在计算斐波那契的过程中出现了大量的子问题重叠过程
解决方法1
记忆化

const int N = 10000;
long long f[N];
long long foi(int n)
{
	if(f[n] != 0)return f[n];
	if(n == 1 || n == 2)return 1;
	else return f[n] = foi(n-1) + foi(n-2);
}

此时你会发现我们用记忆化搜索就可以解决这个问题，为什么还要用动态规划呢，我们会发现我们使用搜索来获取结果是从自顶向下的思考方式去寻找答案。那么我们动态规划又是如何解决问题的呢
解决方案2
动态规划

void dp()
{
    f[1] = 1;f[2] = 1;
    for(int i = 3;i <= n ;i ++)
        f[i] = f[i-1] + f[i-2];
}

此时我们发现根据状态转移方程我们的计算过程是从 1 - n 而我们的记忆化搜索是从 n - > 1 --> n 也就是说这里的动态规划是从自底向上解决问题(当然dp问题不一定都可以用搜索树的形式表示，即: 不是所有的动态规划都可以转化为记忆化搜索问题，而所有的记忆化搜索问题一定可以找到一个状态装一方城转化成动态规划)

动态规划解决问题的步骤

综上我们大致可以总结出解决动态规划问题的一般步骤
1. 寻找最优子结构(状态表示)
2. 归纳状态转移方程(状态计算)
3. 边界初始化

P1216 [USACO1.5][IOI1994]数字三角形 Number Triangles

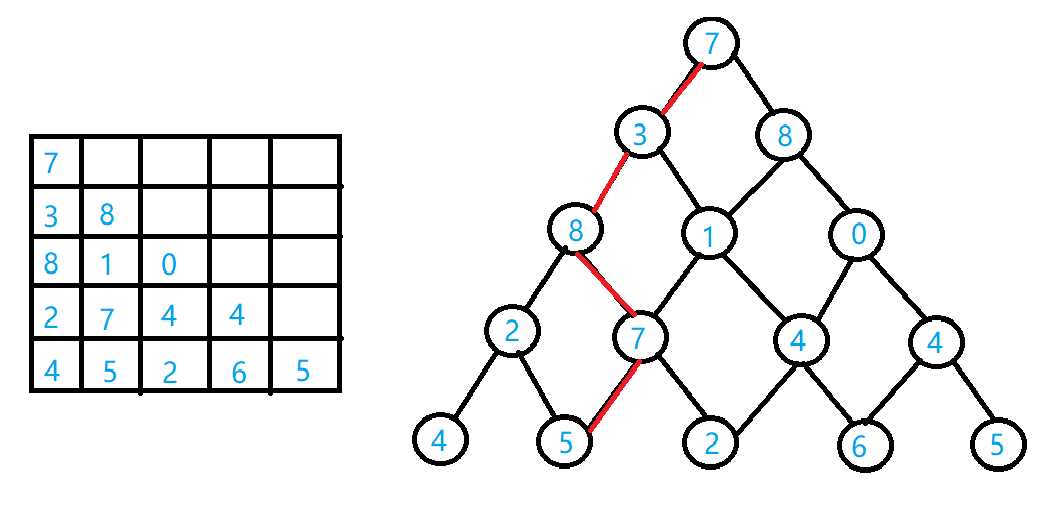
首先我们从搜索的角度去分析问题
加上记忆化优化

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const int N = 10005;
int a[N][N] , f[N][N],n;

int dfs(int x , int y)
{
	if(f[x][y] != 0)return f[x][y];
	if(x == n)return a[x][y];
	int sum = max(dfs(x + 1,y),dfs(x + 1,y + 1));
	return f[x][y] = sum + a[x][y];
} 
int main()
{
	cin >> n;
	for(int i = 1;i <= n ;i ++)
	{
		for(int j = 1;j <= i;j ++)
		{
			scanf("%d",&a[i][j]);
		}
	}
	dfs(1 , 1);
	cout << f[1][1] << endl;	
}

动态规划解法

#include <iostream>
#include <algorithm>
#include <cstdio>

using namespace std;
const int N = 505;
const int INF = 2e9;

int a[N][N] , f[N][N] , n ;
int ans = 0;
// 从上往下推 
void dp()
{
	for(int i = 0;i <= n ;i ++)
	{
		for(int j = 0;j <= i + 1;j ++)
		{
			f[i][j] = -INF;
		}
	}
	f[1][1] = a[1][1];
	for(int i = 2;i <= n ;i ++)
	{
		for(int j = 1;j <= i;j ++)
		{
			f[i][j] = max(f[i-1][j-1],f[i-1][j]) + a[i][j];
		}
	}
	for(int i = 1;i <= n ;i ++)ans = max(ans,f[n][i]);	
}

//从下往上推
 
void dp2()
{
	for(int i = n ;i >= 1;i --)
	{
		for(int j = i;j >= 1 ;j --)
		{
			f[i][j] += max(f[i+1][j],f[i+1][j+1]) + a[i][j];
		}	
	}
	cout << f[1][1] << endl;	
} 
int main()
{
	cin >> n;
	for(int i = 1;i <= n ;i ++)
	{
		for(int j = 1;j <= i ;j ++)
		{
			scanf("%d",&a[i][j]);
		}
	}
	dp();cout << ans << endl; 
	return 0;
}

建议大家去看的视频:
灯神的dp讲解
yx的闫氏dp分析法

动态规划基本思想

标签：splay   可见   步骤   ever   include   using   时间   如何   变形   

原文地址：https://www.cnblogs.com/wlw-x/p/12591363.html