标签:不同的 计算 除了 header 简单的 影响 推断 老婆 img
简单地说,贝叶斯就是你见到贝克汉姆,说了一句yes,研究的是这种概率事件。
开玩笑啦,贝叶斯原理是英国数学家托马斯·贝叶斯提出的,为了解决一个“逆概率”问题。
例如,如果一个男人发现了他老婆手机里暧昧短信 ,计算机他老婆出轨的概率。
现实生活中,我们很难知道事情的全貌,当不能准确预知一个事物本质的时候,但是可以依靠和事物本质相关的事件来进行判断。
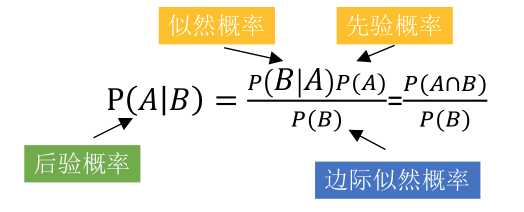
贝叶斯原理类似概率反转,通过先验概率和似然概率,推导出后验概率。
什么是先验概率、似然概率、后验概率?
再以上面出轨的例子为例,
再举个例子,产品由不同的工厂ABC生产,每个工厂都有自己的次品率
似然概率是由假设正推结果,后验概率是由结果倒推假设

\(P(A|B)\):表示事件B已经发生的前提下,事件A发生的概率,叫做事件B发生下事件A的条件概率。
\(P(AB)\):表示事件A和事件B同时发生的概率
\(P(AB)=P(BA)\),可得\(P(AB)=P(BA)=P(B|A)P(A)=P(A|B)P(B)\)
通过\(P(A|B)\)来求\(P(B|A)\),可得\(P(B|A)=\frac {P(A|B)P(B)} {P(A)}\)
分母\(P(A)\)可以根据全概率公式分解为:\(P(A)=\sum_{i=1}^n P(B_i)P(A|B_i)\)
最终公式变为:\(P(B|A)=\frac {P(A|B)P(B)} {\sum_{i=1}^n P(B_i)P(A|B_i)}\)

假设训练数据的属性由n维随机向量x表示,分类结果用随机变量y表示,那x和y的统计规律就可以用联合概率分布\(P(X,Y)\)描述,每个具体的样本\((x_i,y_i)\)都可以通过\(P(X,Y)\)独立同分布地产生。
贝叶斯分类器的出发点是联合概率分布,根据条件概率性质可以得到
\(P(X,Y)=P(Y)?P(X∣Y)=P(X)?P(Y∣X)\)
先验概率很容易计算出来,只需要统计不同类别样本的数目即可,而似然概率受属性数目的影响,估计较为困难。
例如,每个样本包含100个属性,每个属性的取值可能有100种,那分类的每个结果,要计算的条件概率是\(100^2=10000\),数量量非常庞大。因此,这时候引进了朴素贝叶斯

朴素贝叶斯,加了个朴素,意思是更简单的贝叶斯。
朴素贝叶斯假定样本的不同属性满足条件独立性假设,并在此基础上应用贝叶斯定理执行分类任务。
简单地说是
对于给定的待分类项x,分析样本出现在每个类别中的后验概率,将后验概率最大的类作为x所属的类别

要解决似然概率难以估计的问题,就需要引入条件独立性假设。
条件独立性假设保证了所有属性相互独立,互不影响,每个属性独立地对分类结果发生作用。
这样条件概率变成了属性条件概率的乘积
\(P(X=x∣Y=c)=\)
\(P(X(1)=x(1),X(2)=x(2),?,X(n)=x(n)∣Y=c)\)
\(\prod_{j=1}^nP(X^j=x^j|Y=c)\)
这是朴素贝叶斯方法,有了训练数据集,先验概率\(P(Y)\)和你似然概率\(P(X|Y)\)就可以视为已知条件,用来求解后验概率\(P(X|Y)\)。
给定的输入x,朴素贝叶斯分类器利用贝叶斯定理求解后验概率,并将后验概率最大的类作为输出

肌肉是训练、睡眠、饮食多种因素组合的结果
| 训练 | 睡眠 | 饮食 |
|---|---|---|
| 非常好 | 非常好 | 非常好 |
| 好 | 好 | 好 |
| 一般 | 一般 | 一般 |
| 不太好 | 不太好 | 不太好 |
| 不好 | 不好 | 不好 |
| 非常不好 | 非常不好 | 非常不好 |
如果要计算后验概率,假设属性不独立,\(6^3\)就有了216组合,例如其中一种组合是{训练:好,睡眠:不好,包含:一般},这样的组合复杂度太高了
如条件独立互不影响后,只需要考虑3个维度的结果,把最终的属性概率相乘,例如是80%(训练) * 85%(睡眠) * 90%(饮食),算复杂度降低了几个数量级。

受训练数据集规模的限制,某个属性的取值可能在训练集中从未与某个类同时出现,这就可能导致属性条件概率为0,些时直接使用朴素贝叶斯分类就会导致错误的结论。
例如:在训练集中没有样本同时具有“年龄大于 60”的属性和“发放贷款”的标签,那么当一个退休人员申请贷款时,即使他是李嘉诚,朴素贝叶斯分类器也会因为后验概率等于零拒绝。
因为训练集样本的不充分导致分类错误,不是理想的结果,为了避免这种干扰,在计算属性条件概率时需要添加一个“拉普拉斯平滑”的步骤。
拉普拉斯平滑就是计算类先验概率和属性条件概率时,在分子上添加一个较小的修正量,在分母上则添加这个修正量与分类数目的乘积,避免了零概率对分类结果的影响。

属性之间可能具有相关性,而朴素贝叶斯独立假设性会影响分类性能。
半朴素贝叶斯分类器考虑了部分属性之间的依赖关系,既保留了属性之间较强的相关性,又不需要完全计算复杂的联合概率分布。
常用方法是建立独依赖关系:假设每个属性除了类别之外,最多只依赖一个其他属性。
标签:不同的 计算 除了 header 简单的 影响 推断 老婆 img
原文地址:https://www.cnblogs.com/chenqionghe/p/12598786.html