标签：引入   互斥   朴素贝叶斯   aliyun   数据   tail   概率论   有监督   big   

数据挖掘-贝叶斯分类

1. 贝叶斯分类器概述

1.1 贝叶斯分类器简介

1.1.1 什么是贝叶斯分类器？

• 贝叶斯分类器是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类器

1.1.2 朴素贝叶斯分类器

• 朴素贝叶斯分类器是贝叶斯分类器中最简单，也是最常见的一种分类方法。并且，朴素贝叶斯算法仍然是流行的十大挖掘算法之一，该算法是有监督的学习算法，解决的是分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。
• 但由于该算法以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提，就会导致算法精度在某种程度上受影响

2. 数学基础

2.1 概率论

2.1.1 概率

（1）联合概率

• 设\(A，B\)是两个随机事件，A和B同时发生的概率称为联合概率，记为：\(p(A, B)\)
  如果\(A,B\)相互独立，则：\(p(A,B)=p(A)p(B)\)

（2）条件概率

• 在B事件发生的条件下，A事件发生的概率称为条件概率，记为：$ p(A|B)$

  • \(p(A|B)=\frac{p(A,B)}{p(B)}\)
  • \(p(B|A)=\frac{p(A,B)}{p(A)}\)
  • \(p(A|B)p(B)=p(B|A)p(A)=p(A,B)\)

（3）全概率公式

• 对于事件组

  • \(B_1,B_2,...,B_n\)两两互斥，即\(B_i \bigcap B_j=\emptyset,i\not= j,,p(Bi)\not= 0,j=1,2,...,n\),
  • \(B_1\bigcup B_2\bigcup...\bigcup B_n=\Omega\)

  则称\(B_1,B_2,...,B_n\)是样本空间\(\Omega\)的一个划分

• A为任意事件，则:

  • \(p(A) = \sum_{i=1}^np(B_i)p(A|B_i)\)

2.1.2 贝叶斯理论

• 假设有一批样本，\(ω_i\)分别代表不同类别，有样本特征为：\(X=<a_1,a_2,...,a_m>\),（可以理解为在\(ω_i\)类别（原因）下，有特征\(X\)（结果））:

（1）先验概率

• 通过经验来判断事情发生的概率,对于\(ω_i\)来说其先验概率为：\(p(\omega_i)\)

（2）条件概率

• 指当已知类别为\(ω_i\)的条件下，看到结果为样本特征为X的概率

  \(p(X|\omega_i) =\frac{p(\omega_i,X)}{p(\omega_i)}\)

（3）后验概率

• 后验概率就是发生结果之后，即知道样本特征X，推测其类别是\(ω_i\)的概率:

  \(p(\omega_i|X) =\frac{p(X|\omega_i)p(\omega_i)}{p(X)}\)

（4）贝叶斯公式

• \(p(\omega_i|X) =\frac{p(\omega_i)p(X|\omega_i)}{p(X)}=\frac{p(\omega_i)p(X|\omega_i)}{\sum_{i=1}^cp(\omega_i)p(X|\omega_i)}\)

先验概率，后验概率，似然估计

3. 贝叶斯决策论

3.1 贝叶斯决策

3.1.1 贝叶斯决策介绍

• 贝叶斯决策就是利用贝叶斯理论进行决策分类，是统计机器学习的基本方法之一
• 模式识别的问题里，我们只能够观察到一系列的特征\(x=[x1,x2,...,xn]^T\)，在统计机器学习里面,对这一系列的观察值进行分类,求解概率\(P(ω_i|x)\)，可以理解为在观察到特征x的前提下，观察到的现象属于ωi类的概率是多大

3.2 基于最小错误率的贝叶斯决策

3.2.1 什么时候会分错类？

• 当某一特征向量X只为某一类物体所特有时：

  \(p(\omega_k|X)=\begin{cases} 1 , k = i\0 , k \not= i \end{cases}\)

  • 对其作出决策是容易的，也不会出什么差错

• 当某一特征向量X为不同类物体所特有时,即几种类别中均有可能出现该特征，时会有分错情况

3.2.2 基于最小错误率的贝叶斯分类器

• 基于最小错误概率的贝叶斯决策理论就是按后验概率的大小作判决的

（1） 后验概率

若：\(p(\omega_i|X)=\max_{j=1,2}p(\omega_j|X)\),则：\(X\in \omega_i\)

• 例
  • 
  • 

（2）比较分子

• 由2.1.2 （3）可知，当X特征一致时，其后验概率大小比较即分母的大小比较
• 所以：若：\(p(X|\omega_i)p(\omega_i)=\max_{j=1,2}p(x|\omega_i)p(\omega_i)\)，则：\(X \in \omega_i\)

（3）似然比

• 若：\(l(x)=\frac{p(x|\omega_1)}{p(x|\omega_2)}>\frac{p(\omega_2)}{p(\omega_1)}\)，则：\(X\in \omega_1\)；否则：\(X\in \omega_2\)

（4）将似然比转换成负对数形式

• 若：\(h(X)=-\ln(l(x))=-\ln(p(X|\omega_1)+\ln(p(X|\omega_2)))>\ln\frac{p(\omega_1)}{p(\omega_2)}\)，则：\(X\in \omega_1\)；否则：\(X\in \omega_2\)

3.2.3 基于最小错误率的贝叶斯决策的证明

（1）证明步骤

1. 当采用最大后验概率分类器时，分类错误的概率为：

   \(p(e)=\int_{-\infty}^{+\infty}p(error,x)dx=\int_{-\infty}^{+\infty}p(error|x)p(x)dx\)

2. 而在已知特征X的情况下，出现错误推测分类的概率为：

   \(p(error|x)=\sum_{i=1}^cp(\omega_i|x)-\max_{1\leq j \leq c }p(\omega_j|x)\)

3. 当p(w2|x)>p(w1|x)时决策为w2，对观测值x有 p(w1|x)概率的错误率：

   \(p(e|x)=\begin{cases} p(x|\omega_1),当p(x|\omega_1)<p(x|\omega_2)\p(x|\omega_2),当p(x|\omega_2)<p(x|\omega_1) \end{cases}\)

4. 设：

   • R_1:做出w1决策的所有观测值区域，条件错误概率为p(w2|x)
   • R_2:做出w2决策的所有观测值区域，条件错误概率为p(w1|x)。

5. 因此平均错误率p(e)可表示成：

   \(p(e)=\int_{R_1} p(\omega_2|x)p(x)dx+\int_{R_2}p(\omega_1|x)p(x)dx\)

3.2.4 分类决策边界

（1）分类决策边界

• 分类决策边界：$p(ω_i|x) = p(ω_j|x) $,即出现X特征，使得将该事务分类到两方的概率相同
  

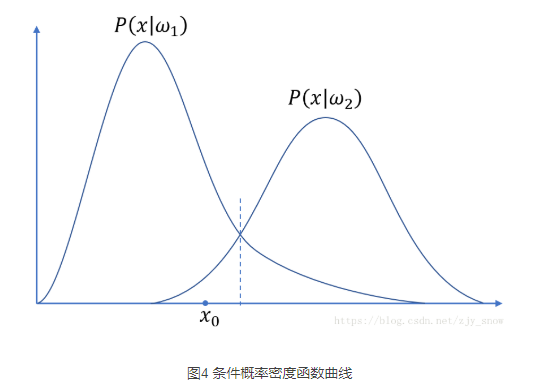
• 分类决策边界不一定是线性的，也不一定是连续的
  

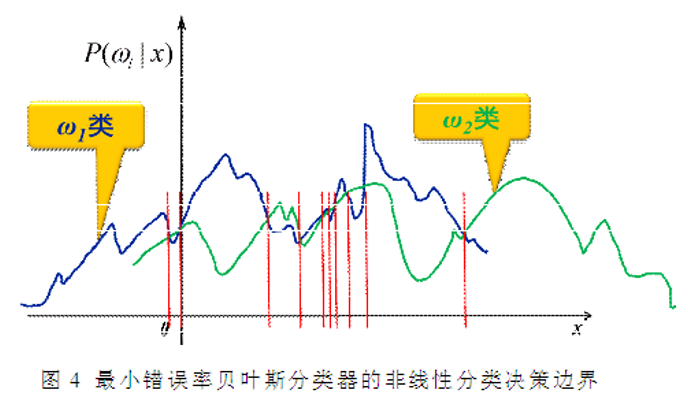
（2）错误率

• 错误率为下图中两个划线部分之和，对应的错误率区域面积为最小
  

3.2 基于最小风险的贝叶斯决策

3.2.1 为什么引入基于最小风险的贝叶斯决策?

• 在最小错误贝叶斯分类器分类器中,仅考虑了样本属于每一类的后验概 率就做出了分类决策,而没有考虑每一种分类决策的风险。
• 事实上,在许多模式识别问题中,即使样本属于两类的后验概率相同,将其分到每一类中所带来的风险也会有很大差异。

3.2.2 基于最小风险的贝叶斯决策

• 获得样本属于每一类的后验概率后,需要综合考虑做出各种分类决策所带来的风险,选择风险最小的分类决策,称为最小风险贝叶斯分类器。
• 贝叶斯决策论：
  • 前提：所有相关概率已知
  • 关注点：误判损失
• 为了使风险减小，就需要移动图4中虚线的位置，要使得风险更大的那类错误分类更小，如下图所示（\(\omega_2\)的风险要大于\(\omega_1\),所以需要将决策面倾向于分类成\(\omega_2\)）
  

3.2.3 决策标准

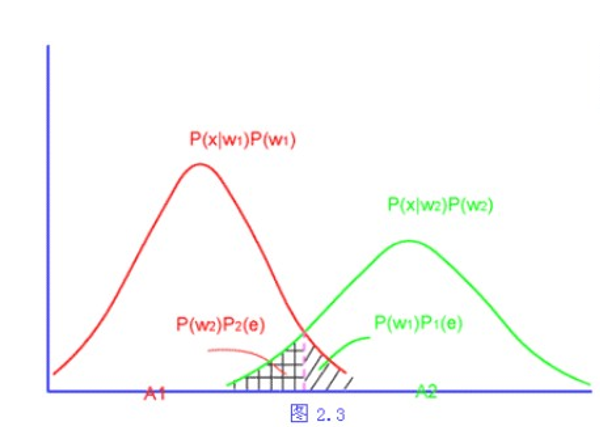
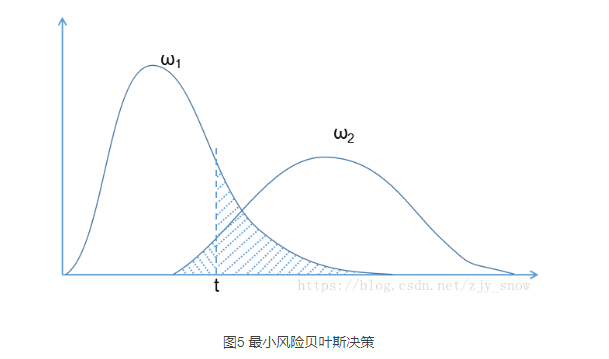
（1）自然状态

• 指待识别对象的类别

  \(A=\{a_1,a_2,...,a_k\}\)

（2）状态空间

• 由所有自然状态所组成的空间

  \(\Omega=\{\omega_1,\omega_2,...,\omega_c\}\)

（3）决策与决策空间

• 决策：不仅包括根据观测值将样本划归为哪一类别（状态），还可包括其他决策，如"拒绝"等
• 决策空间：由所有决策组成的空间

（4）决策风险函数λ(α,ω)

• 指对于实际状态为\(wj\)的向量\(x\)采取决策\(a_i\)所带来的损失\(\lambda(a_i,\omega_j),i=1,...,k,j=1,...,c\)

  也写作：\(\lambda(a_i|\omega_j)\)

  • j并不一定等于c（可能包含“拒绝”等决策）

（5）期望损失（风险）

• 在N种可能的标记种，\(λ_{ij}\)是指将\(ω_j\)误分为\(ω_i\)时所产生的损失。基于后验概率：\(P（ω_i|x）\)得到误分为\(C_i\)时所产生的期望损失，这个损失也叫做”风险“，当我们制定一个准则\(h\)使得对于每一个样本\(x\)风险最小时（此时整个样本的总体风险\(R（h*）\)（贝叶斯风险）也达到最小），称h为贝叶斯最优分类器

  \(R_i(X)=R(\omega_i|X)=\sum_{j=1}^c\lambda_j^{i}p(\omega_j|X)\)

  • \(R_i\)则表示了观测值\(x\)被判为\(i\)类时损失的均值
  • 分类则依据\(Ri,(i=1,...,c)\)中的最小值，即最小风险来定

3.2.4 最小风险贝叶斯决策的计算步骤

• 对于一个实际问题，对于样本\(x\)，最小风险贝叶斯决策的计算步骤如下：

1. 利用贝叶斯公式计算后验概率：

   \(p(\omega_i|X) =\frac{p(\omega_i)p(X|\omega_i)}{p(X)}=\frac{p(\omega_i)p(X|\omega_i)}{\sum_{i=1}^cp(\omega_i)p(X|\omega_i)}\)

2. 利用决策表，计算条件风险：

   \(R_i(X)=R(\omega_i|X)=\sum_{j=1}^c\lambda(a_i,\omega_j))p(\omega_j|X)\)

3. 决策：选择风险最小的决策，即:

   \(a=\arg\min_{i=1,...,k}R(a_i|X)\)

数据挖掘-贝叶斯分类器

标签：引入   互斥   朴素贝叶斯   aliyun   数据   tail   概率论   有监督   big   

原文地址：https://www.cnblogs.com/nishoushun/p/12600413.html