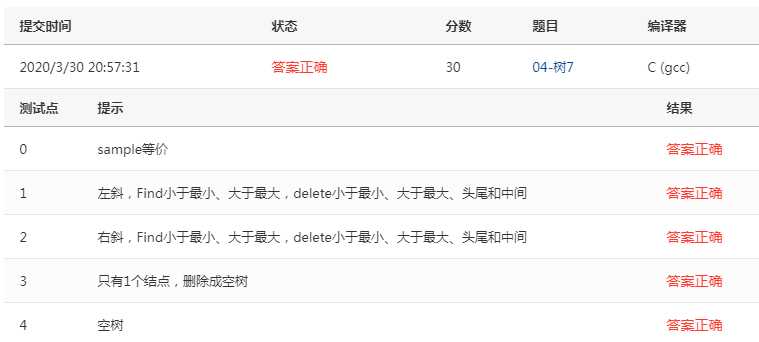
标签:选择 int 二叉树 printf == lse 数据 数据结构 写法
BinTree Insert( BinTree BST, ElementType X ){
if(BST==NULL){
BST = (BinTree)malloc(sizeof(struct TNode));
BST->Left = NULL;
BST->Right = NULL;
BST->Data = X;
return BST;
}
BinTree pre,p;
p = BST;
pre = BST;
while(p != NULL){
if(X > p->Data){
pre = p;
p = p->Right;
}
else if(X < p->Data){
pre = p;
p = p->Left;
}
else return BST;
}
p = (BinTree)malloc(sizeof(struct TNode));
p->Left =NULL;
p->Right = NULL;
p->Data = X;
if(X > pre->Data) pre->Right = p;
else pre->Left = p;
return BST;
}
Position Find( BinTree BST, ElementType X ){
BinTree p;
p = BST;
while(p!=NULL){
if(p->Data == X){
return p;
}
else if(p->Data >X) p = p->Left;
else p = p->Right;
}
return NULL;
}
Position FindMin( BinTree BST ){
if(BST==NULL) return NULL;
BinTree p;
p = BST;
while(p->Left!=NULL) p = p->Left;
return p;
}
Position FindMax( BinTree BST ){
if(BST==NULL) return NULL;
BinTree p;
p = BST;
while(p->Right!=NULL) p = p->Right;
return p;
}
BinTree Delete( BinTree BST, ElementType X ){
if(BST==NULL){
printf("Not Found\n");
return BST;
}
if(X > BST->Data) BST->Right = Delete(BST->Right,X);
else if(X < BST->Data) BST->Left = Delete(BST->Left,X);
else{
if(BST->Left!=NULL && BST->Right!=NULL){
BinTree p ;
p = FindMin(BST->Right);
BST->Data = p->Data;
BST->Right = Delete(BST->Right,p->Data);
}else if(BST->Left==NULL && BST->Right == NULL){free(BST);return NULL;}
else
{
BinTree temp=BST;
if(BST->Left!=NULL) BST = BST->Left;
if(BST->Right!=NULL) BST = BST->Right;
free(temp);
}
}
return BST;
}
注意:1.二叉搜索树的含义;(二叉排序树、二叉查找树)
2.在增加、删除、查找时的递归写法;
3. 删除时,如果遇到左右子树都不为空的情况,可以选择两种方案(左子树找最大值所在的位置;右子树找最小值所在的位置)
4.对于二叉搜索树来说,为了使插入元素后仍能保持在O(logn)的级别,可以采用平衡二叉树,左右子树的高度之差的绝对值不超过1。
数据结构-1 二叉搜索树的操作集
标签:选择 int 二叉树 printf == lse 数据 数据结构 写法
原文地址:https://www.cnblogs.com/Learn-Excel/p/12601165.html