标签:root ofo list 结构 方式 span 超过 arch src
typedef struct LNode *List; struct Lnode { ElementType Element[MaxSize]; int length; };
静态查找:
方法1:顺序查找(时间复杂度为O(n))
int SequentialSearch (List Tbl, ElementType K){ //在Element[1] - Element[n]中查找关键字为K的数据元素 int i; Tbl->Element[0] = K; //建立哨兵 for (i=Tbl->length; Tbl->Element[i] != K; i--); return i; //查找成功返回所在单元下标,不成功返回0 } 无哨兵 int SequentialSearch (List Tbl, ElementType K){ //在Element[1] - Element[n]中查找关键字为K的数据元素 int i; for (i=Tbl->length; i>0 && Tbl->Element[i] != K; i--); return i; //查找成功返回所在单元下标,不成功返回0 }
方法2:二分查找(时间复杂度为O(logN))
int BinarySearch (List Tbl, ElementType K){ //在表Tbl中查找关键字为K的数据元素 int left, right, mid, NoFound = -1; left = 1; //初始左边界 right = Tbl->length; //初始右边界 while (left <= right) { mid = (left+right) / 2; //计算中间元素坐标 if (K < Tbl->Element[mid]) right = mid -1; //调整右边界 else if (K > Tbl->Element[mid]) left = mid + 1; //调整左边界 else return mid; //查找成功,返回数据元素的下标 } return NotFound; //查找不成功,返回-1 }
二分查找判定树:
(1)判定树上每个节点需要查找的次数刚好为该结点所在的层数;
(2)查找成功时查找次数不会超过判定树的深度
(3)n个结点的判定树的深度为[log2n]+1
(树)是非线性数据结构。
树:n个结点构成的有限集合
当n = 0时,称为空树
对于任一颗非空树,他具备以下性质:
(1)树中有一个称为“根(Root)”的特殊节点,用r表示
(2)其余结点可分为m个互不相交的有限集Ti,称为原来树的“子树(subTree)”
(3)子树是不相交的
(4)除根节点外,每个结点有且仅有一个父结点
(5)一棵N个结点的树有N-1条边
(6)树是保证结点连通的最小的连接方式
树的一些基本术语:
(1)结点的度:结点的子树个数
(2)树的度:树的所有结点中最大的度数
(3)叶结点:度为0的结点
(4)父结点:有子树的结点是其子树的根节点的父结点
(5)子结点:若A结点是B结点的父结点,则称B结点是A结点的子结点;子结点也称孩子节点
(6)兄弟结点:具有同一父结点的各节点彼此是兄弟结点
(7)路径和路径的长度:路径所包含边的个数为路径的长度
(8)祖先结点:沿树根到某一结点路径上的所有结点都是这个结点的祖先结点
(9)子孙结点:某一结点的子树中的所有结点是这个结点的子孙
(10)结点的层次:规定根节点在1层,其他任一结点的层数是其父结点的层数加1
(11)树的深度:树中所有结点中的最大层次是这棵树的深度
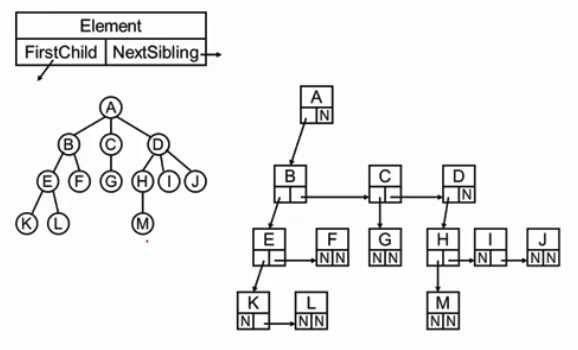
树的表示
儿子-兄弟表示法:每一个结构都是统一的,空间浪费不大,真正空的域为n+1
标签:root ofo list 结构 方式 span 超过 arch src
原文地址:https://www.cnblogs.com/zhengxin909/p/12609125.html