标签:解决 比较 port 修改 lse proc 运算 操作符 ldb
结对项目成员:软三 陈纪禧(3118005043)、软三 程伟杰(3118005045)
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
60 |
|
|
· Estimate |
· 估计这个任务需要多少时间 |
60 |
|
|
Development |
开发 |
1680 |
|
|
· Analysis |
· 需求分析 (包括学习新技术) |
120 |
|
|
· Design Spec |
· 生成设计文档 |
30 |
|
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
10 |
|
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
20 |
|
|
· Design |
· 具体设计 |
120 |
|
|
· Coding |
· 具体编码 |
1200 |
|
|
· Code Review |
· 代码复审 |
60 |
|
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
120 |
|
|
Reporting |
报告 |
150 |
|
|
· Test Report |
· 测试报告 |
60 |
|
|
· Size Measurement |
· 计算工作量 |
30 |
|
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
60 |
|
|
合计 |
|
1890 |
|
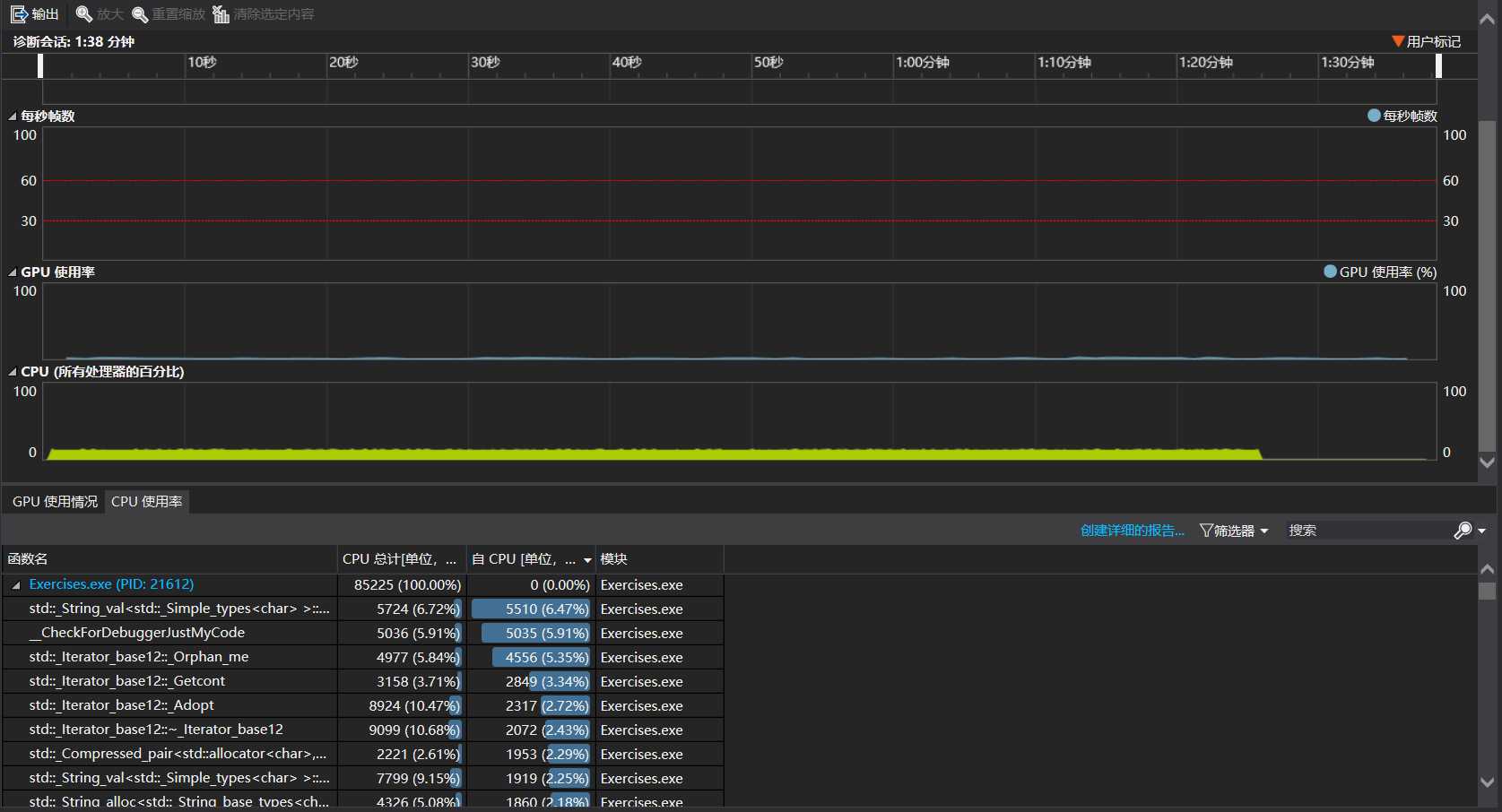
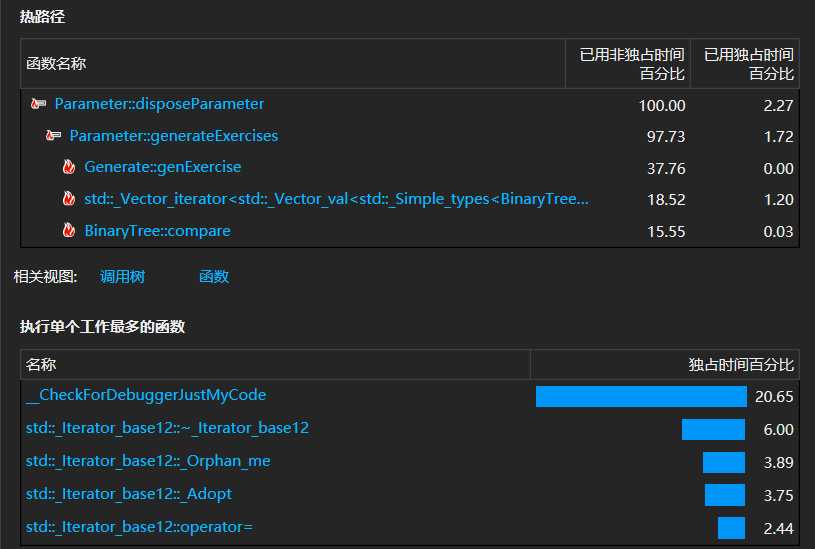
分析:由效能分析易知,判重函数占用程序时间最多,后续优化可从这方面入手。
设计6个类,不同类实现不同功能,说明如下:
Parameter //处理命令行中传来的参数
Generate //生成表达式
Statistics //统计类,对于给定题目答案的对错进行统计
BinaryTree //二叉树类
Calculator //计算类
Fraction //分数类,所有运算数都是此类型
类与函数的调用关系图:(注:调用→被调用)
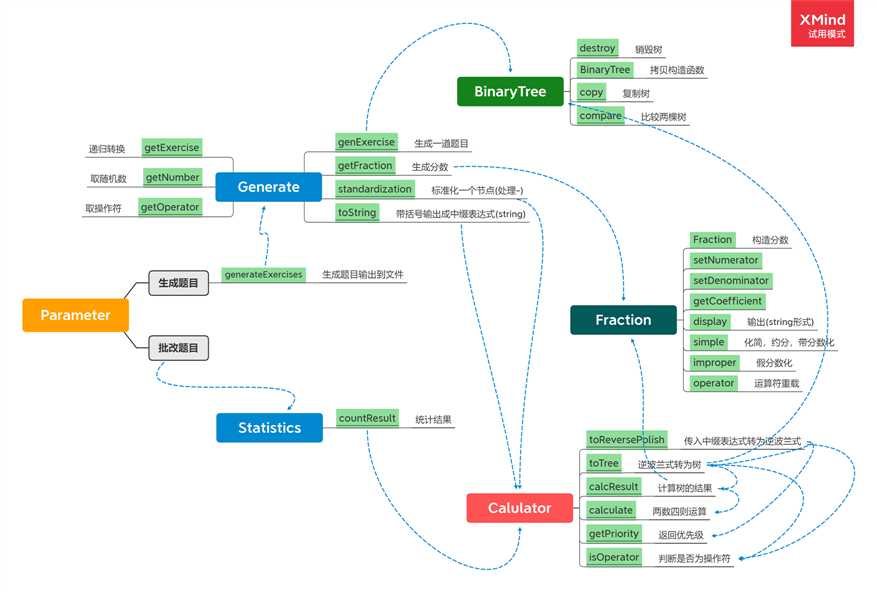
表达式查重:
1 void Parameter::generateExercises(int num, int range) 2 { 3 if (num == 0 || range == 0) 4 return; 5 6 //打开文件 7 exercises.open("Exercises.txt", std::ios::out | std::ios::trunc); 8 answers.open("Answers.txt", std::ios::out | std::ios::trunc); 9 if (!exercises.is_open() || !answers.is_open()) 10 return; 11 12 //每生成一个表达式都与其他元素比较,不重复就入组 13 vector<BinaryTreeNode *> exe; //用于存放表达式树 14 exe.reserve(num); //预留空间避免过多扩容 15 16 vector<BinaryTreeNode *>::iterator ite; 17 Generate *generate = generate = new Generate(range); 18 BinaryTree *tree = nullptr; 19 bool flag = false; //标志是否重复 20 21 for (int i = 0; i < num; i++) //生成num个 22 { 23 do 24 { 25 tree = generate->genExercise(); 26 for (ite = exe.begin(); ite != exe.end(); ite++) 27 { 28 flag = BinaryTree::compare(tree->pRoot, *ite); 29 if (flag == true) //匹配到重复就跳出判断,避免标志被更改 30 { 31 //重复就删除生成的树 32 delete tree; 33 tree = nullptr; 34 break; 35 } 36 } 37 } while (flag == true); 38 39 if (flag == false) //未重复就push 40 { 41 exe.push_back(tree->pRoot); 42 } 43 } 44 45 for (int i = 0; i < (int)exe.size(); i++) 46 { 47 string strExercises = generate->getExercise(exe.at(i)); 48 exercises << i + 1 << "." << strExercises.c_str() << endl; 49 50 //转成计算器计算结果避免出错 51 BinaryTreeNode *result = Calculator::toTree(Calculator::toReversePolish(strExercises)); 52 string strAnswers = Calculator::calcResult(result).display(); 53 answers << i + 1 << "." << strAnswers.c_str() << endl; 54 } 55 56 cout << "题目与答案已写入到文件" << endl; 57 58 delete generate; 59 //关闭文件 60 exercises.close(); 61 answers.close(); 62 }
Generate类 //生成表达式
表达式建树:
1 BinaryTree * Generate::genExercise() 2 { 3 //3 --> 2 --> 2 4 // -> 3 --> 1 5 6 //运算符个数 7 std::uniform_int_distribution<int> opeCount(1, 3); 8 int opeNum = opeCount(mt); 9 10 //先新建出一颗最小树 11 BinaryTreeNode *left = new BinaryTreeNode(getFraction().display()); 12 BinaryTreeNode *right = new BinaryTreeNode(getFraction().display()); 13 string *data = new string(1, getOperator()); 14 BinaryTreeNode *root = new BinaryTreeNode(*data, left, right); 15 standardization(root); 16 opeNum--; 17 18 if (opeNum == 0) //如果运算符只有一个直接返回 19 { 20 BinaryTree *tree = new BinaryTree(root); 21 return tree; 22 } 23 24 //用于二选一的随机数 25 std::uniform_int_distribution<int> randBool(0, 1); 26 27 //选择下一步是2或3 28 if (randBool(mt) == 0 && opeNum == 2) //再生成一个最小树并连接 29 { 30 left = new BinaryTreeNode(getFraction().display()); 31 right = new BinaryTreeNode(getFraction().display()); 32 data = new string(1, getOperator()); 33 BinaryTreeNode *tempRoot = new BinaryTreeNode(*data, left, right); 34 standardization(tempRoot); 35 opeNum--; 36 37 //选择左右顺序 38 if (randBool(mt) == 0) //新树在左 39 { 40 left = tempRoot; 41 right = root; 42 } 43 else 44 { 45 left = root; 46 right = tempRoot; 47 } 48 //连接 49 data = new string(1, getOperator()); 50 root = new BinaryTreeNode(*data, left, right); 51 standardization(root); 52 opeNum--; 53 54 BinaryTree *tree = new BinaryTree(root); 55 return tree; 56 } 57 else //往上插 58 { 59 do 60 { 61 //二选一 左上or右上 62 if (randBool(mt) == 0) //左上 63 { 64 left = new BinaryTreeNode(getFraction().display()); 65 right = root; 66 } 67 else //右上 68 { 69 left = root; 70 right = new BinaryTreeNode(getFraction().display()); 71 } 72 data = new string(1, getOperator()); 73 root = new BinaryTreeNode(*data, left, right); 74 standardization(root); 75 opeNum--; 76 } while (opeNum > 0); 77 78 BinaryTree *tree = new BinaryTree(root); 79 return tree; 80 } 81 return nullptr; 82 }
表达式加括号:
1 bool Generate::toString(BinaryTreeNode * root, string &strExercise) 2 { 3 if (root == nullptr) 4 { 5 return true; 6 } 7 8 bool lChildBracket = false, rChildBracket = false; //标志括号 9 int leftPriority = 0, curPriority = 0, rightPriority = 0; //优先级 10 11 //中序遍历 12 if (root->leftChild != nullptr) 13 { 14 //左子树是操作符加括号 15 if (Calculator::isOperator(root->leftChild->data.at(0))) 16 { 17 //得到优先级 18 leftPriority = Calculator::getPriority(root->leftChild->data.at(0)); 19 curPriority = Calculator::getPriority(root->data.at(0)); 20 if (leftPriority == 0 || curPriority == 0) 21 { 22 return false; 23 } 24 if (curPriority > leftPriority) //优先级大加括号 25 { 26 strExercise = strExercise + "("; 27 lChildBracket = true; 28 } 29 } 30 //遍历左子树 31 toString(root->leftChild, strExercise); 32 //补上括号 33 if (lChildBracket == true) 34 { 35 strExercise = strExercise + ")"; 36 lChildBracket = false; 37 } 38 } 39 40 //中 41 if (Calculator::isOperator(root->data.at(0))) 42 strExercise = strExercise + " " + root->data + " "; 43 else 44 strExercise = strExercise + root->data; 45 46 //右 47 if (root->rightChild != nullptr) 48 { 49 //右子树是操作符加括号 50 if (Calculator::isOperator(root->rightChild->data.at(0))) 51 { 52 //得到优先级 53 rightPriority = Calculator::getPriority(root->rightChild->data.at(0)); 54 curPriority = Calculator::getPriority(root->data.at(0)); 55 if (rightPriority == 0 || curPriority == 0) 56 { 57 return false; 58 } 59 if (curPriority > rightPriority) //优先级大加括号 60 { 61 strExercise = strExercise + "("; 62 rChildBracket = true; 63 } 64 } 65 //遍历右子树 66 toString(root->rightChild, strExercise); 67 //补上括号 68 if (rChildBracket == true) 69 { 70 strExercise = strExercise + ")"; 71 rChildBracket = false; 72 } 73 } 74 return true; 75 }
Calculator //计算类
传入中缀表达式转为逆波兰式:
1 string Calculator::toReversePolish(string expression) //传入中缀表达式转为逆波兰式 2 { 3 std::stack<string> S1; //运算符栈 4 std::stack<string> S2; //逆波兰式栈 5 string *ope; //运算符,分数 6 string *exp = new string; //逆波兰式 7 string *leftbracket = new string(1, ‘(‘); //左括号 8 9 for (int i = 0; i < expression.length(); i++) //从expression中逐个取出字符 10 { 11 if (isOperator(expression.at(i))) //若取出运算符 12 { 13 if (S1.empty() || expression.at(i) == ‘(‘) 14 { 15 ope = new string(1, expression.at(i)); 16 S1.push(*ope); 17 } 18 else if(expression.at(i) == ‘)‘) 19 { 20 ope = new string; 21 *ope = S1.top(); S1.pop(); 22 while ((*ope).at(0) != ‘(‘) //取出‘(‘后停止循环,并抛弃‘(‘ 23 { 24 if ((*ope).at(0) != ‘(‘) 25 { 26 S2.push(*ope); 27 } 28 ope = new string; 29 *ope = S1.top(); S1.pop(); 30 } 31 i++; 32 } 33 else if (getPriority(expression.at(i)) > getPriority(S1.top().at(0))) //比较优先级 34 { 35 ope = new string(1, expression.at(i)); 36 S1.push(*ope); //该运算符优先级比栈顶运算符优先级高,直接入栈 37 } 38 else 39 { 40 if (!S1.empty()) 41 { 42 while (getPriority(expression.at(i)) <= getPriority(S1.top().at(0))) 43 { //从运算符栈S1逐个取出运算符并压入表达式栈S2,直到该运算符优先级比栈顶运算符优先级高 44 ope = new string; 45 *ope = S1.top(); S1.pop(); 46 S2.push(*ope); 47 if (S1.empty()) break; 48 } 49 } 50 ope = new string(1, expression.at(i)); 51 S1.push(*ope); //完成操作后该运算符优先级比栈顶运算符优先级高,入运算符栈S1 52 } 53 } 54 else 55 { 56 if (expression.at(i) == ‘ ‘) i++; //隔离第一个空格 57 string fat; 58 while (expression.at(i) != ‘ ‘ && expression.at(i) != ‘(‘ && expression.at(i) != ‘)‘) 59 { //保存分数字符串 60 fat.push_back(expression.at(i)); 61 i++; 62 if (i >= expression.length()) break; 63 } 64 if (!fat.empty()) 65 { 66 S2.push(fat); //生成分数字符串,并压入表达式栈S2 67 } 68 if (i < expression.length()) 69 { 70 if (expression.at(i) == ‘(‘ || expression.at(i) == ‘)‘) i--; 71 } 72 } 73 } 74 while (!S2.empty()) //将表达式栈逆序 75 { 76 string op; 77 op = S2.top(); S2.pop(); 78 S1.push(op); 79 } 80 exp = new string; 81 while(!S1.empty()) //组装逆波兰式 82 { 83 string str = S1.top(); S1.pop(); 84 if (!S1.empty()) 85 { 86 *exp = *exp + str + ‘ ‘; 87 } 88 else 89 { 90 *exp = *exp + str; 91 } 92 } 93 return *exp; //返回逆波兰式 94 }
逆波兰式转为树:
1 BinaryTreeNode * Calculator::toTree(string exp) //逆波兰式转为树 2 { 3 std::stack<BinaryTreeNode*> num; //数字栈 4 BinaryTreeNode *exp_ptr = nullptr; //结点指针 5 BinaryTreeNode *right = nullptr; //右孩子指针 6 BinaryTreeNode *left = nullptr; //左孩子指针 7 string *data_exp; //结点数据 8 9 for (int i = 0; i < exp.length(); i++) //逐个字符读取逆波兰式 10 { 11 if (isOperator(exp.at(i))) //读取到运算符 12 { 13 right = num.top(); num.pop(); 14 left = num.top(); num.pop(); 15 data_exp = new string(1,exp.at(i)); //将运算符转化为string类型,并赋给结点数据data 16 17 BinaryTreeNode *exp_root = new BinaryTreeNode(*data_exp, left, right); //构建新树 18 num.push(exp_root); 19 } 20 else 21 { //读取到数字,生成完整分数字符串,并压入数字栈num 22 if (exp.at(i) == ‘ ‘) i++; //隔离第一个空格 23 if (!isOperator(exp.at(i))) 24 { 25 string fat; 26 while (exp.at(i) != ‘ ‘) 27 { //保存分数字符串 28 fat.push_back(exp.at(i)); 29 i++; 30 if (i >= exp.length()) break; 31 } 32 exp_ptr = new BinaryTreeNode; 33 if (!fat.empty()) 34 { 35 exp_ptr->data = fat; 36 num.push(exp_ptr); 37 } 38 } 39 else 40 { 41 i--; 42 } 43 } 44 } 45 exp_ptr = num.top(); num.pop(); //从栈顶取出建好的树的根结点 46 return exp_ptr; //返回树的根结点 47 }
1.生成一万道题目与答案:
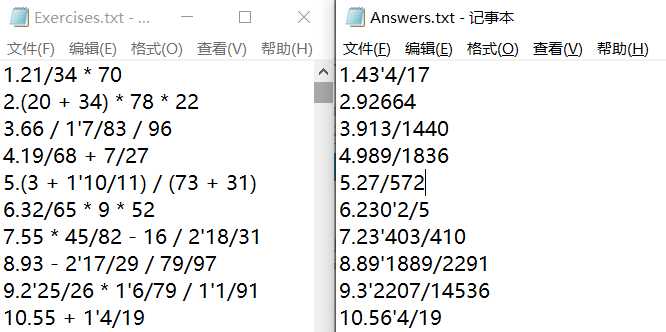
2.批改一万道题目:

3.修改1,4,6题的答案再次批改:


|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
60 |
90 |
|
· Estimate |
· 估计这个任务需要多少时间 |
60 |
90 |
|
Development |
开发 |
1680 |
1600 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
120 |
160 |
|
· Design Spec |
· 生成设计文档 |
30 |
30 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
10 |
10 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
20 |
20 |
|
· Design |
· 具体设计 |
120 |
120 |
|
· Coding |
· 具体编码 |
1200 |
1080 |
|
· Code Review |
· 代码复审 |
60 |
60 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
120 |
120 |
|
Reporting |
报告 |
150 |
120 |
|
· Test Report |
· 测试报告 |
60 |
30 |
|
· Size Measurement |
· 计算工作量 |
30 |
30 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
60 |
60 |
|
合计 |
|
1890 |
1810 |
开发初:
本来我们想使用VS上的插件live share进行结对项目的开发,但后面发现这个插件不符合我们的想法,后转用Github团队仓库进行开发。
遇到的一大困难是对Github团队仓库的使用,仔细研究之后才初步学会使用,了解了分支、更改、同步、拉取、推送等功能,解决难题后也算是一大收获。
项目本身:
由于我们两人编程水平相差较大,纪禧很强而伟杰只有c语言基础,开发过程比较坎坷。后来也是通过不断交流,不断翻阅博客,终于实现了这个项目。
优点:前期结构框架定得很好,所以后续实现和改动比较方便。
难点:中缀表达式转逆波兰式建树的过程中需要考虑的因素很多,对各种情况的判断及解决比较复杂,刚写好时总是出现越界问题,后用断点不断调试,终于改好。
结对感受:
合作比单人更有动力,交流更多,犯错更少,学到的东西也更多,更迅速。
标签:解决 比较 port 修改 lse proc 运算 操作符 ldb
原文地址:https://www.cnblogs.com/clsgghost/p/12605005.html