标签:利用 思想 多项式 函数 数字 log 计算 表示 输入
??(1) 将时域动态指标 超调量σ、上升时间tr 及 峰值时间ts转换为z域指标阻尼比ξ、自然频率wn 及 -ξwn ;
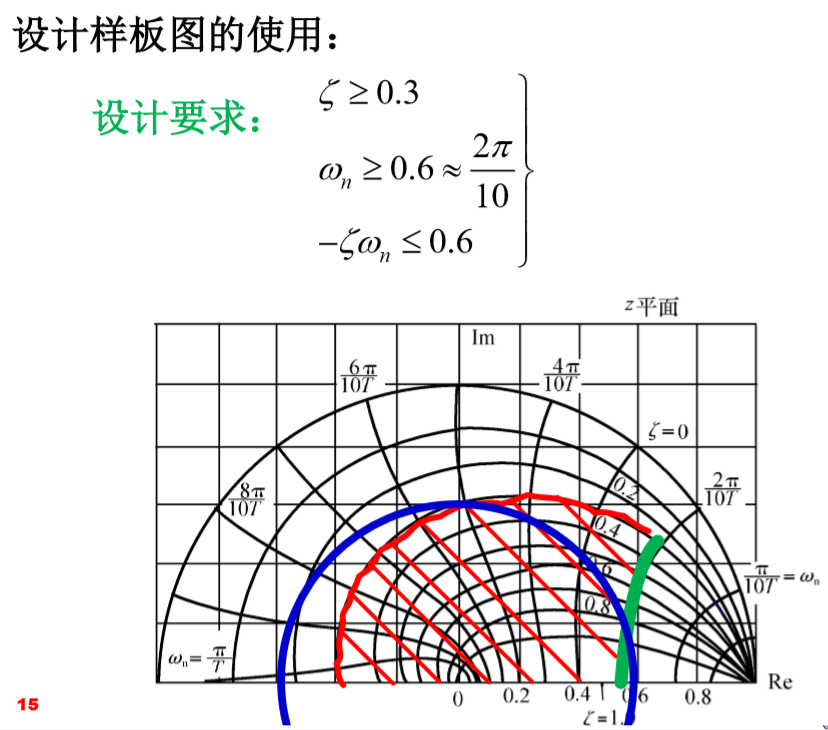
??(2)利用z域指标结合 设计样板图 绘制出特殊区域;
??(3)设计D(z) ,使得 完整系统 的根轨迹经过该特殊区域即可。( 根轨迹方程(1+D(z)G(z) , 注意G(z)为广义被控对象,即 G(z) = ZOH*Go(z) )

??由自动控制原理I知识可以知道,某些高阶系统,可以近似为二阶系统:

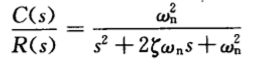
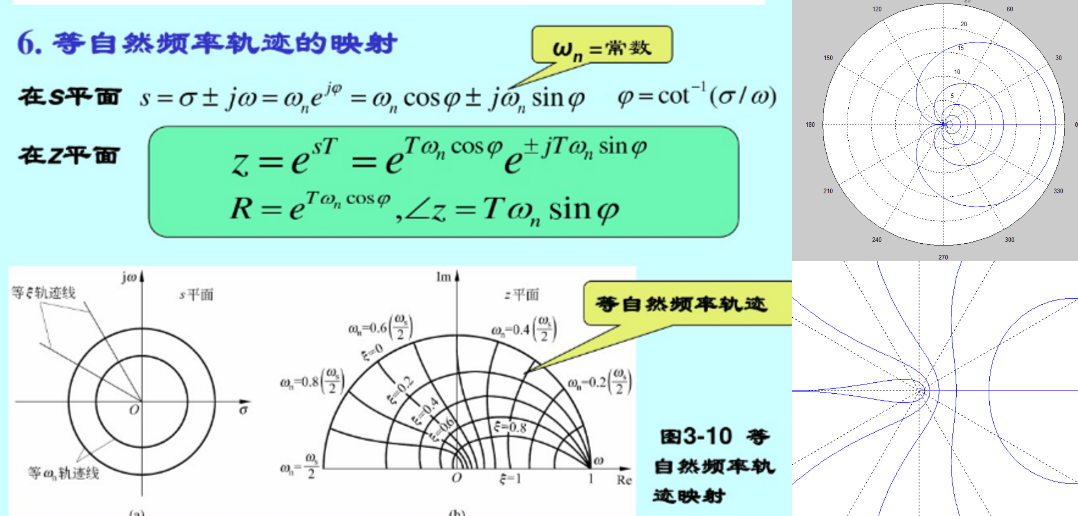
??经过一系列推导可以得到指标转换关系:

??设计样板图 绘制在 z平面,包含 等阻尼比ξ螺旋线、等自然频率wn线 及以 r = e-ξwn为半径的圆周曲线:

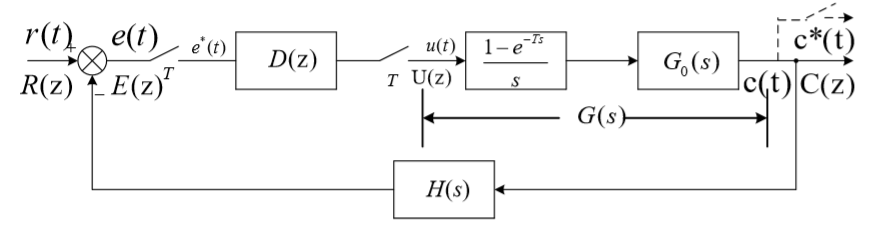
??对于如下典型系统方框图:
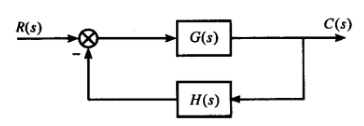
??其闭环传递函数为:
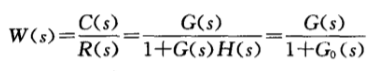
??其开环传递函数的零极点形式如下:
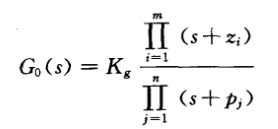
??上式中 Kg 称为 根轨迹增益,通常所述的 开环增益K 为:
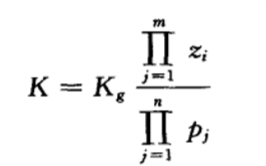
??特别注意,上式不计零值极点,零点个数为0时分子记为1。
??幅值条件:
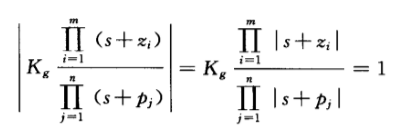
??幅角条件:
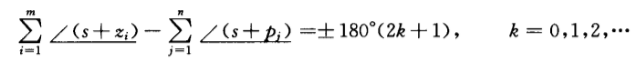
??(i) 起点和终点
????起于极点,终于零点。
??(ii) 分支数
????等于开环极点数。
??(iii) 对称性
????关于复平面实轴对称。
??(iv) 渐近线
????渐近线方程:
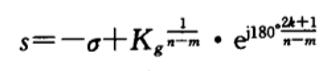
????渐近线与实轴交点:
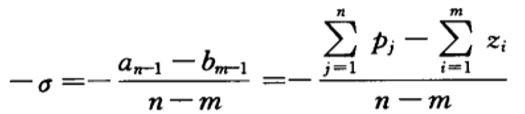
????渐近线与实轴夹角:
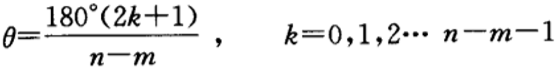
??(v) 实轴上的根轨迹
?? ?? 当根轨迹增益Kg为正数时,实轴上的点若在根轨迹上,则其右方实轴上的开环零点数和极点数的和必为奇数。
??(vi) 实轴上的分离点和汇合点

??(vii) 复平面上的出射角和入射角
?? ??根轨迹趋于开环零点-p1的出射角:
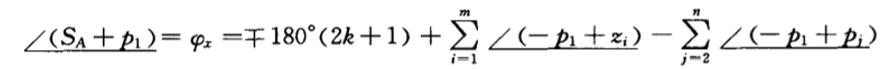
?? ??根轨迹趋于开环零点-z1的入射角:
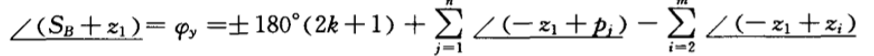
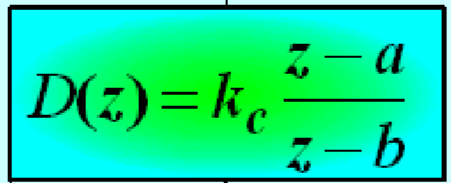
?? 以例题进行叙述较为直观:

?? 以下为解题过程:


??本课程不讲解,故不作讨论。
??核心思想:将期望的闭环系统行为预先确定下来,用公式表示出来, 再通过代数解法,求出控制器的传递函数。通常理想的系统为无纹波、无稳态误差的最少拍系统。
??对于如下系统:
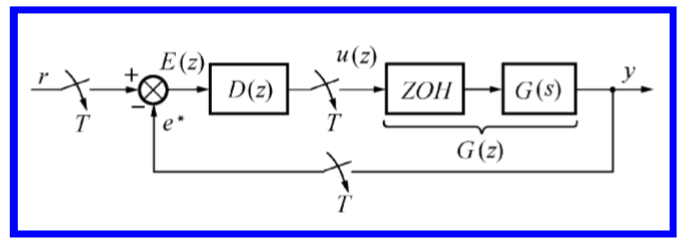
??其闭环特征传递函数H(z):
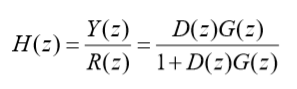
??得数字控制器传递函数D(z):
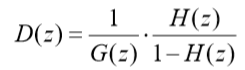
??从上式可以看出 D(z)的解析法设计主要需要考虑H(z)和1-H(z)的形式 。
??所谓物理可实现性,即要求系统为因果系统。体现在:
??H(z)应为z-1的多项式,即
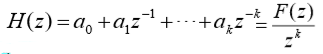
??1-H(z)应具有如下形式:
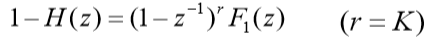
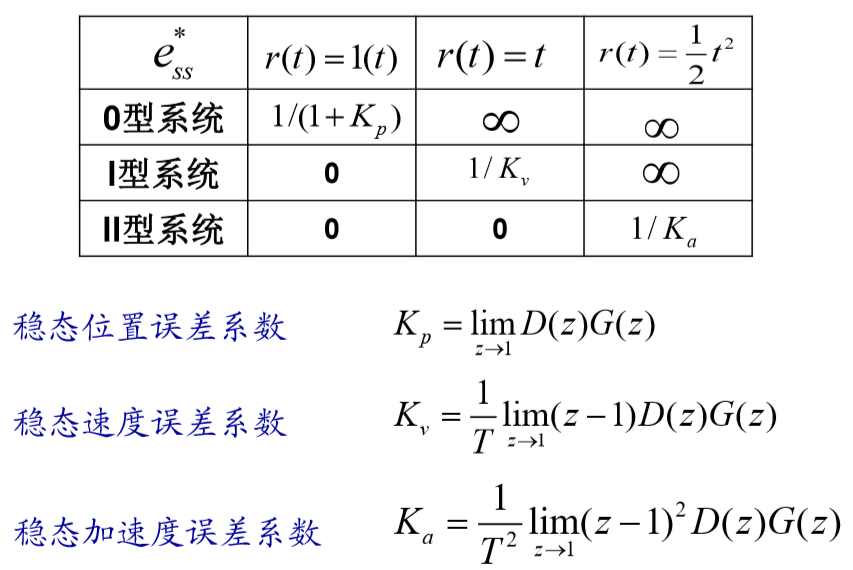
?? 其中K为输入信号的型别:
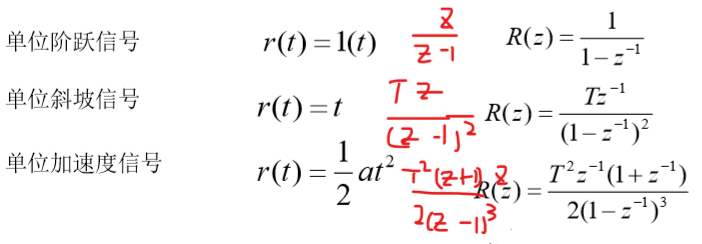
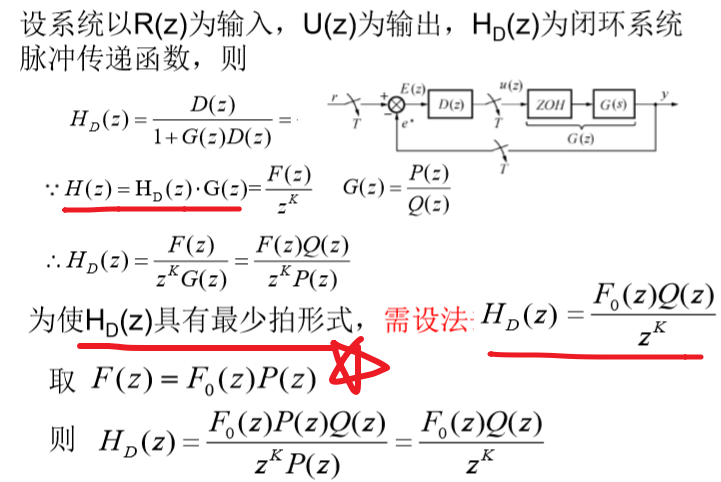
??如下所示:
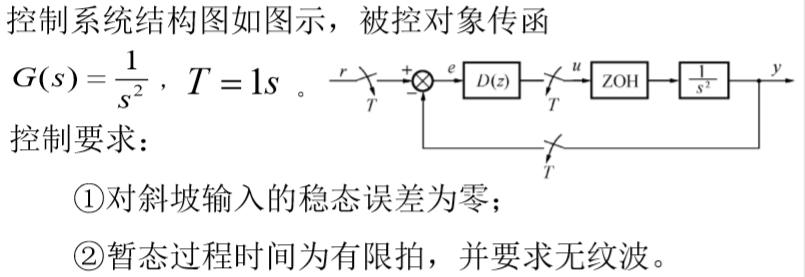
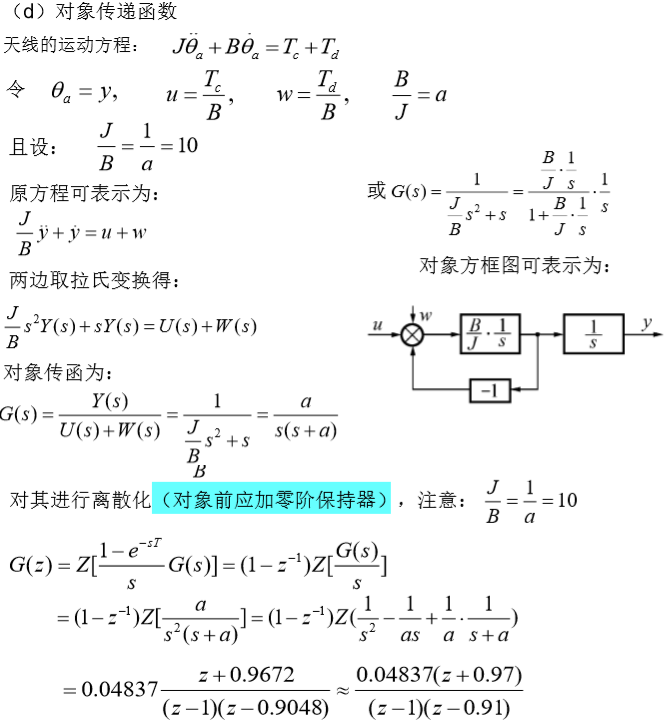
??(0) 离散化广义被控对象G(s)
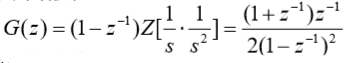
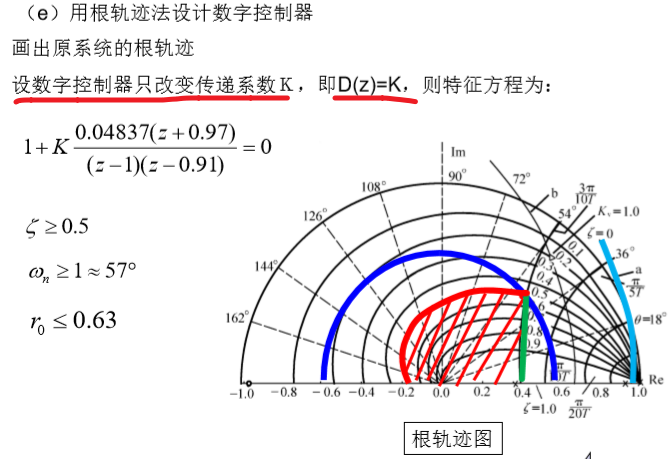
??(i) D(z)的物理可实现性
????由式可知,D(z)只要求分母阶次>=分子阶次即可。
??(ii) 系统稳定性
????H(z)的零点中应包含G(z)中不稳定的零点:
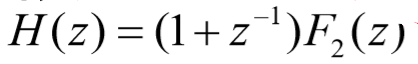
????1-H(z)的零点中应包含G(z)中不稳定的极点:
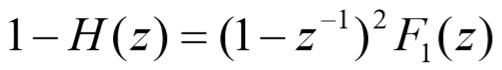
??(iii) 最少拍系统
????H(z)应为z-1的多项式,即
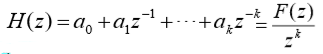
??(iv)对特定信号稳态误差为零
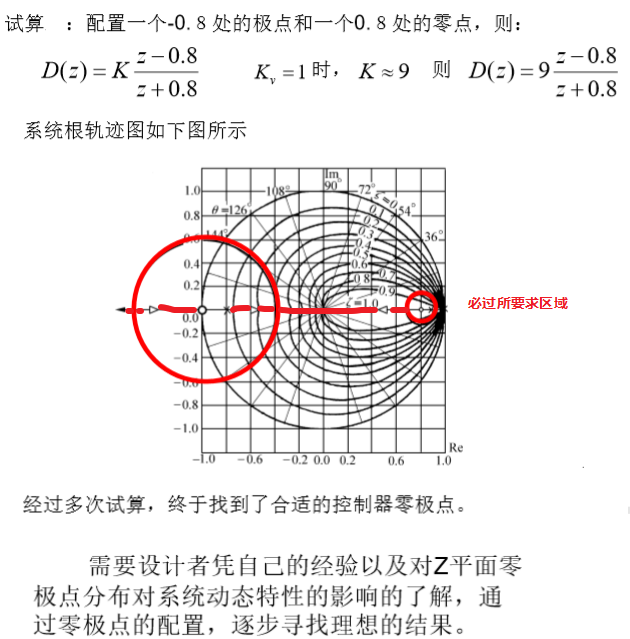
????由于输入信号为斜坡信号,因此有:
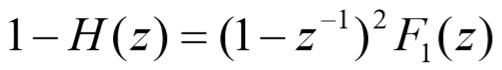
??(v)无纹波
????H(z)应包含G(z)的分子多项式。故有:
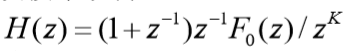
????且余项(F0(z) / zk)也为最少拍形式,故取K = 1,得:
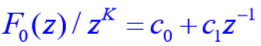
??(vi)综合求解
????由(ii)(iii)(v),得 H(z) :
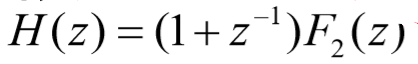
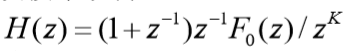
????观察可知 F2(z) = z-1F0(z) / zk,得:
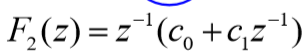

????由上式,得 1-H(z):
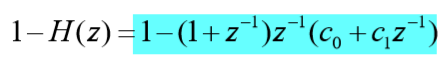
????由(ii)(iv),得 1-H(z) 形式:
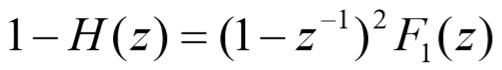
????为使使H(z)和1-H(z) 中 z-1的最高阶次相等,取:
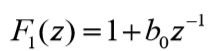
????故:
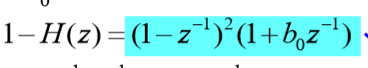
????对比两蓝色区域所示部分,应有:
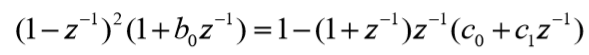
????比较系数,解方程组:
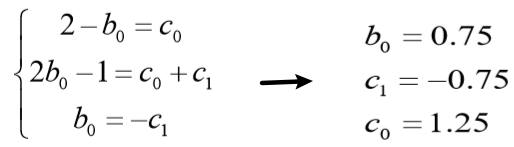
????带入H(z)和1-H(z):
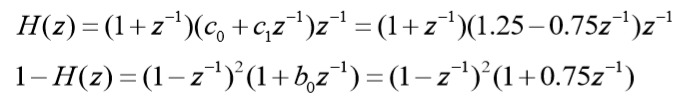
????得D(z):
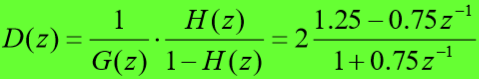
????进而得计算机控制式:
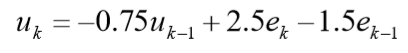
标签:利用 思想 多项式 函数 数字 log 计算 表示 输入
原文地址:https://www.cnblogs.com/beta-1999/p/12622877.html