标签:href mamicode log img 集合 推广 次数 get archive
参考了:Matrix67 - 经典证明:Prüfer编码与Cayley公式
是一种挺有意思的转化
~ Prufer编码 ~
Prufer编码,是一种对于带标号无根树的编码,使得一个Prufer序列$p$能够唯一对应一棵带标号无根树,且不重不漏
编码方式是这样的:
对于一棵$n$个节点的带标号无根树($n\geq 2$),我们每次找到标号最小的叶节点,将其所连接的非叶节点的标号添加进序列,然后删去这个叶节点;不断这样循环,直到剩余节点数为$2$
由于这个做法将$n$个节点的树删成$2$个节点,所以得到的Prufer序列的长度为$n-2$
引用Matrix67的例子:对于以下带标号无根树求Prufer序列
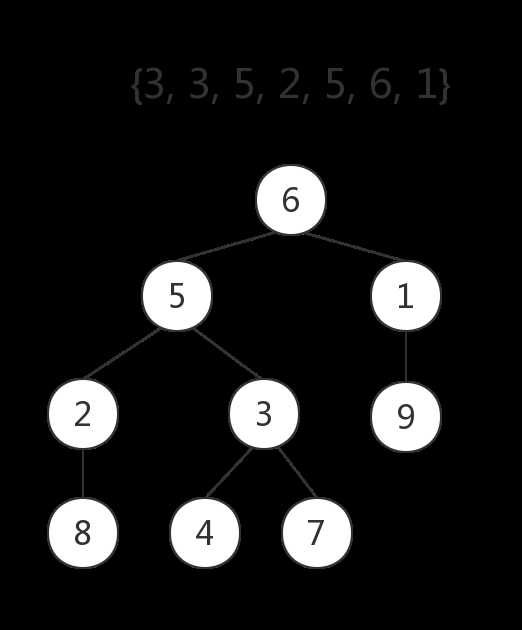
1. 先把所有叶节点全部拎出来,发现为$\{4,7,8,9\}$,其中节点$4$最小,于是将节点$4$所连接的非叶节点$3$加入序列、并删去节点$4$;序列$p$暂时为$\{3\}$
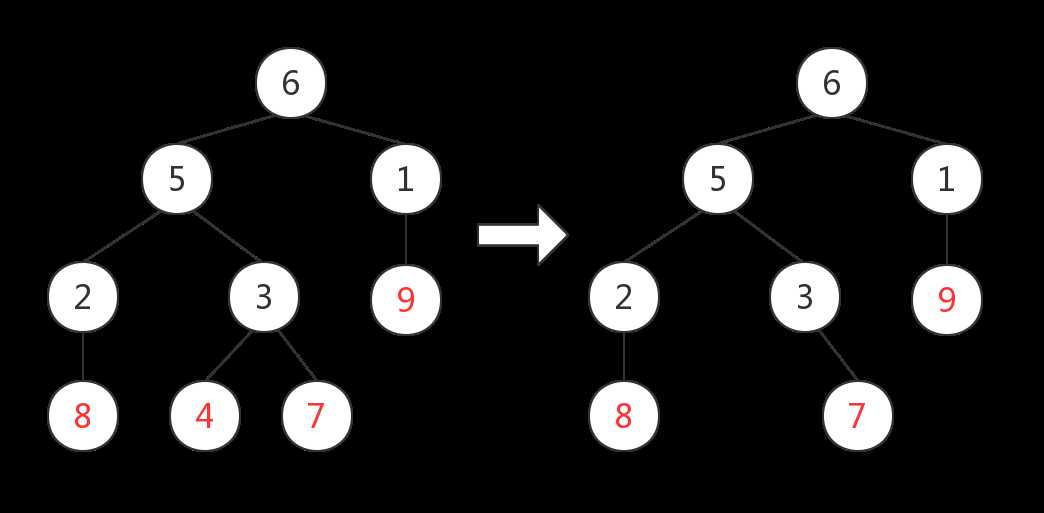
2. 此时的叶节点有$\{7,8,9\}$,将$7$所连接的非叶节点$3$加入序列、并删去节点$7$;序列$p$暂时为$\{3,3\}$
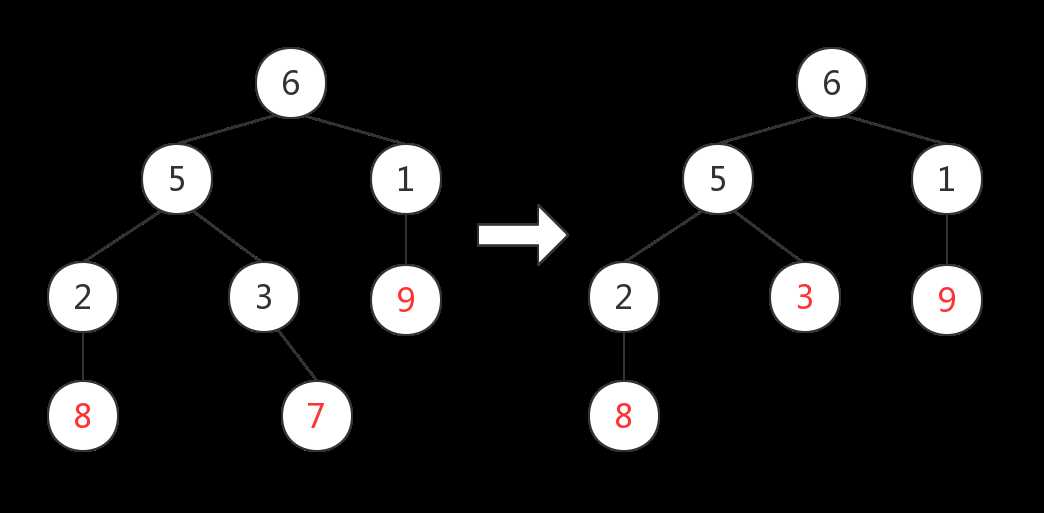
3. 此时的叶节点有$\{3,8,9\}$,将节点$3$所连接的非叶节点$5$加入序列、并删去节点$3$;序列$p$暂时为$\{3,3,5\}$
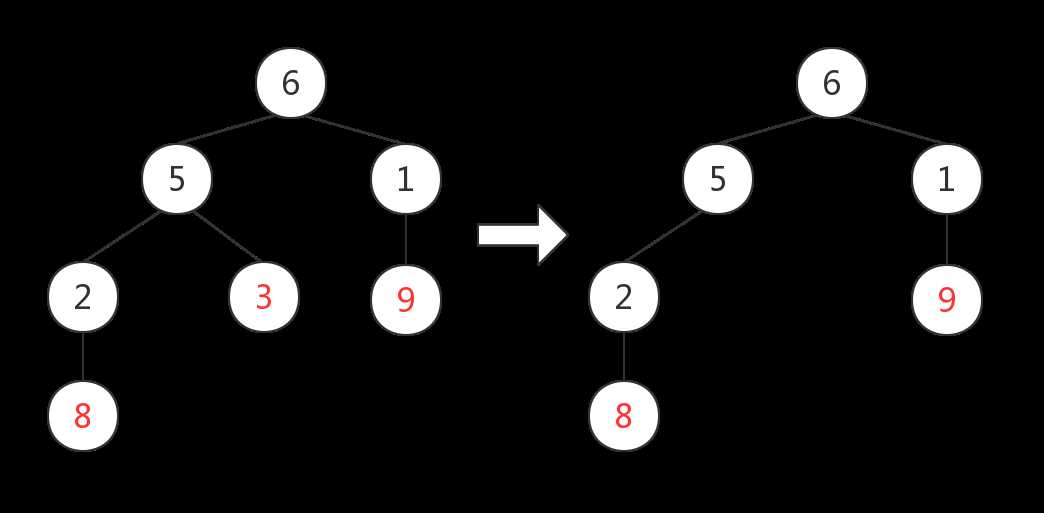
4. 之后不断重复这个过程,最终得到Prufer序列$p=\{3,3,5,2,5,6,1\}$
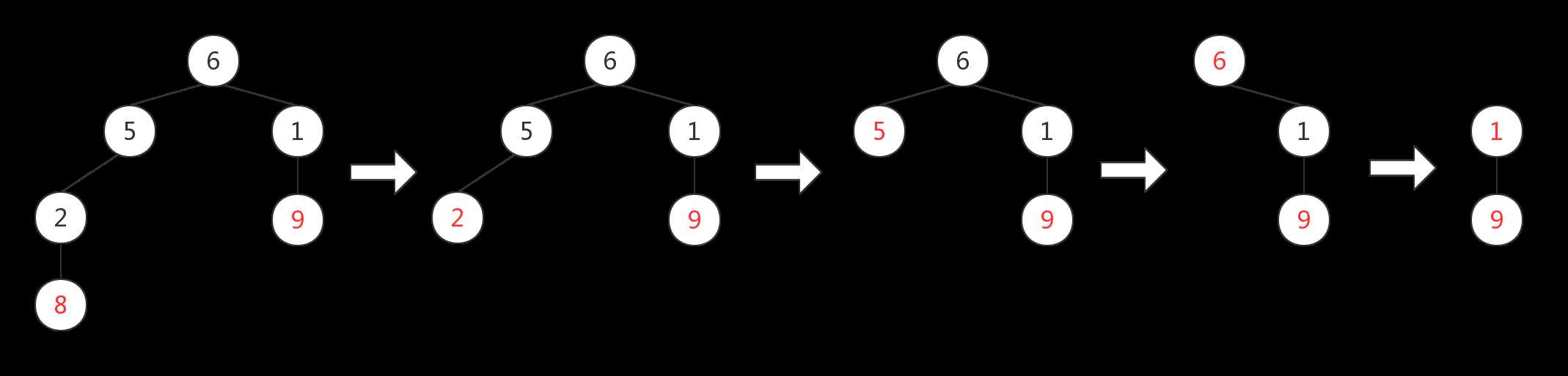
上面我们提到了 一个Prufer序列唯一对应一棵有标号的无根树
那么给定一个Prufer序列时,如何构造对应的树呢?其实和上面的做法是十分类似的
首先我们有一个性质:在Prufer序列$p$中的节点为无根树中的非叶节点,不在$p$中的节点为叶节点
这是显然的,因为叶节点只会被删去,而每次加入序列的点都是叶节点所连接的非叶节点
然后可以将这个性质稍加推广:在子序列$p[i...n-2]$中的节点为操作过$i-1$次的无根树中的非叶节点,不在$p$中、且未被前$i-1$次操作删去的节点为叶节点
这又可以推出另一个性质:Prufer序列所确定的无根树,节点$i$的度数等于$i$在Prufer序列中出现次数+1
那么我们可以维护当前无根树的叶节点集合,而集合中的最小元素就是将被删去的叶节点
multiset<int> nleaf,leaf; for(int i=1;i<=n-2;i++) nleaf.insert(p[i]); for(int i=1;i<=n;i++) if(nleaf.find(i)==nleaf.end()) leaf.insert(i); for(int i=1;i<=n-2;i++) { printf("%d %d\n",*leaf.begin(),p[i]); leaf.erase(leaf.begin()); nleaf.erase(nleaf.find(p[i])); if(nleaf.find(p[i])==nleaf.end()) leaf.insert(p[i]); } printf("%d %d\n",*leaf.begin(),*(++leaf.begin()));
利用Prufer序列,我们尝试证明Cayley公式
Cayley公式指的是,$n$阶完全图$K_n$有$n^{n-2}$棵生成树;或者说$n$个节点的带标号无根树有$n^{n-2}$棵
这里的幂次$n-2$让我们很眼熟,因为这恰是Prufer序列的长度;那么$n^{n-2}$就代表着,$n-2$个位置任意填$[1,n]$中的数,都可以构成Prufer序列
事实上也确实是这样的,因为我们总能保证叶节点集合的大小至少为$2$——在$p[i...n-2]$中出现的非叶节点数加上已删去的$i-1$个叶节点最多只有$n-2$个,剩余的至少$2$个节点均为当前无根树的叶节点;所以这$n^{n-2}$个序列均为合法的Prufer序列
而一个Prufer序列唯一对应一个带标号无根树,那么Cayley公式得证
还有一个奇妙的结论是,一个度数序列为$\{d_1,d_2,...,d_n\}$的带标号无根树共有$\frac{(n-2)!}{\prod_{i=1}^{n} (d_i-1)!}$棵
证明比较容易:
一个度数序列为$d_i$的节点必会在Prufer序列中出现$d_i-1$次,那么不妨从$i=1$开始计算;要满足$1$号节点的度数为$d_1$,就需要在Prufer序列的$n-2$个位置中选$d_1-1$个填$1$,则有$\begin{pmatrix} n-2\\d_1-1\end{pmatrix}$中选法;而$i=2$时需要从剩余的$(n-2)-(d_1-1)$个位置中选$d_2-1$个,有$\begin{pmatrix} (n-2)-(d_1-1)\\d_2-1\end{pmatrix}$……将组合数用阶乘展开,就是$\frac{(n-2)!}{(d_1-1)![(n-2)-(d_1-1)]!}\cdot \frac{[(n-2)-(d_1-1)]!}{(d_2-1)![(n-2)-(d_1-1)-(d_2-1)]!}\cdot ...$,即为上面的结论
~ 一些题目 ~
BZOJ 1005 (明明的烦恼,$HNOI2008$)
HDU 5629 ($Clarke\ and\ tree$)
CF 156D ($Clues$)
ZOJ 4069 ($Sub-cycle\ Graph$,$2018ICPC$青岛)
CF 917D ($Stranger\ Tree$)
Luogu P5219 (无聊的水题)
还要生成函数+NTT,那就咕了
(待续)
标签:href mamicode log img 集合 推广 次数 get archive
原文地址:https://www.cnblogs.com/LiuRunky/p/Prufer_Sequence.html