标签:print 分类 ssis i+1 操作 ons 固定 opera other
Dreamoon likes coloring cells very much.
There is a row of nn cells. Initially, all cells are empty (don‘t contain any color). Cells are numbered from 11 to nn .
You are given an integer mm and mm integers l1,l2,…,lml1,l2,…,lm (1≤li≤n1≤li≤n )
Dreamoon will perform mm operations.
In ii -th operation, Dreamoon will choose a number pipi from range [1,n−li+1][1,n−li+1] (inclusive) and will paint all cells from pipi to pi+li−1pi+li−1 (inclusive) in ii -th color. Note that cells may be colored more one than once, in this case, cell will have the color from the latest operation.
Dreamoon hopes that after these mm operations, all colors will appear at least once and all cells will be colored. Please help Dreamoon to choose pipi in each operation to satisfy all constraints.
The first line contains two integers n,mn,m (1≤m≤n≤1000001≤m≤n≤100000 ).
The second line contains mm integers l1,l2,…,lml1,l2,…,lm (1≤li≤n1≤li≤n ).
If it‘s impossible to perform mm operations to satisfy all constraints, print "‘-1" (without quotes).
Otherwise, print mm integers p1,p2,…,pmp1,p2,…,pm (1≤pi≤n−li+11≤pi≤n−li+1 ), after these mm operations, all colors should appear at least once and all cells should be colored.
If there are several possible solutions, you can print any.
5 3 3 2 2
2 4 1
10 1 1
-1
虽然想了挺长时间才想出来,不过起码做出来了2333看了眼题解貌似做法不太一样..?
首先要明白这个题想让我们干什么。仔细读题看清楚这些转化关系后就会发现,这道题实际上属于贪心里的区间覆盖类问题,(只不过和常见的几类区间覆盖问题不一样)最终是要构造出一组pi,使得1~n这个区间被覆盖,且每个区间都要有露在外面的部分,而每个区间长度是固定的li。这样就完成了题面的转化。
在这里放一张图帮助理解(渣图轻喷)。
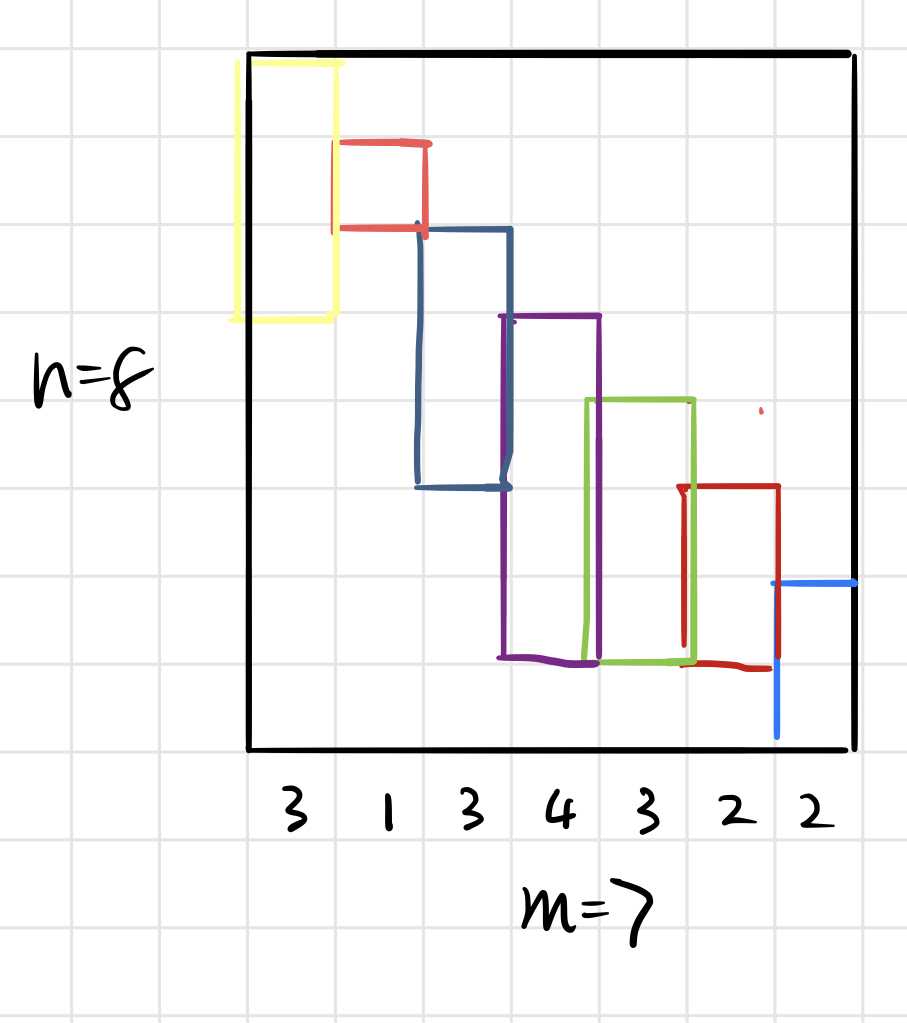
那么问题来了,该怎么选择贪心策略呢?这里我的切入点是这么一句话:Note that cells may be colored more one than once, in this case, cell will have the color from the latest operation.这意味着在后面涂的颜色会覆盖掉前面的,即最后一种颜色区间可以随便排…这样引导我们从后往前考虑。a[i]代表l[i],b[i]代表p[i](这样稍微好看一点),top代表目前已经覆盖的长度(从后往前的顺序),例如对于上面的图i=3时top=5。
以下是意识流题解:首先设想最理想的一种情况,即每种颜色的区间露出的长度都为1,如下图。
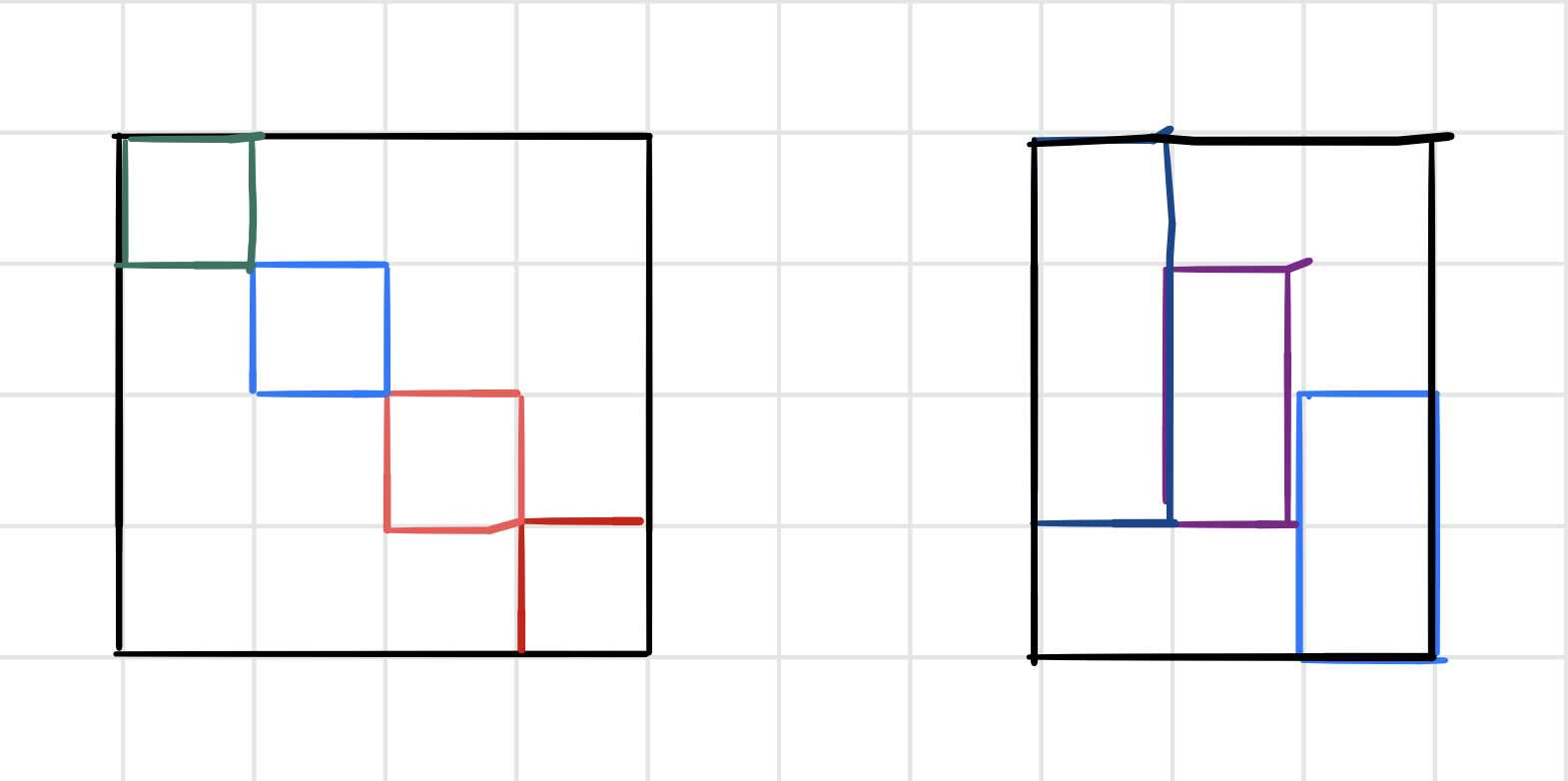
当然实际情况不一定有这么完美,所以这时候我选择的贪心策略就是:在当前区间填完后尽可能让剩下的情况变得更“完美”。
具体操作如下:
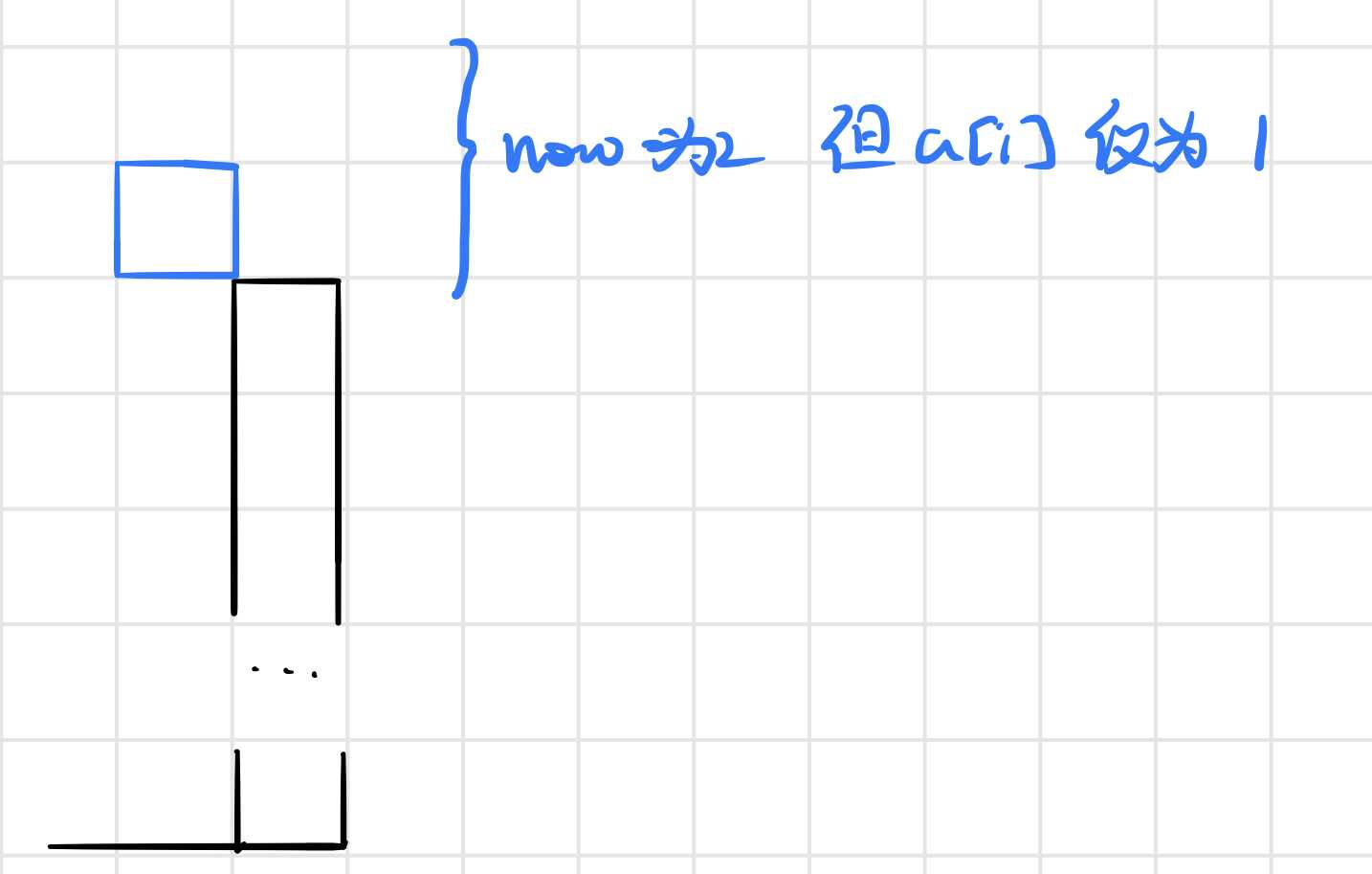
首先,因为是从后往前遍历(i:m~1)因此当遍历到i时(i这种颜色还没开始涂),首先判断剩余颜色数目和剩余区间长度的关系,如果剩余颜色数目更大的话肯定不行(有的颜色一定被覆盖);如果剩余区间长度更大(或者两者相等),这时就要分类讨论了。先求出为使剩下情况变得完美当前区间需要露出来的长度,即now=n-top-(res-1),如果i颜色恰好能满足这种
要求(如下图这几种情况都满足now=2时)
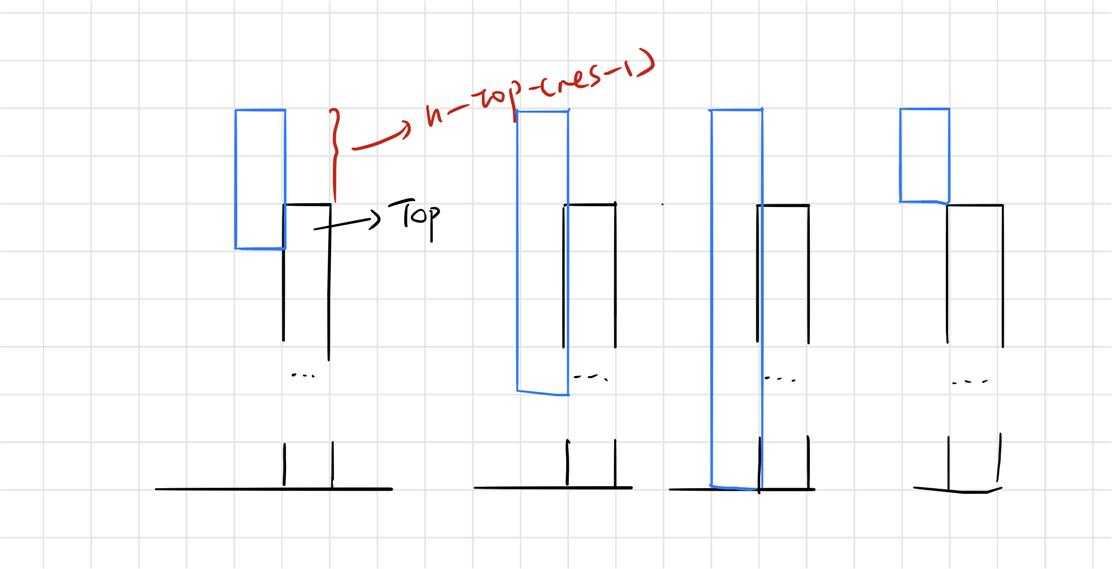
那么就能确定i这种颜色怎么涂了。执行 b[i]=(now+top-a[i]+1); top+=now;即可。
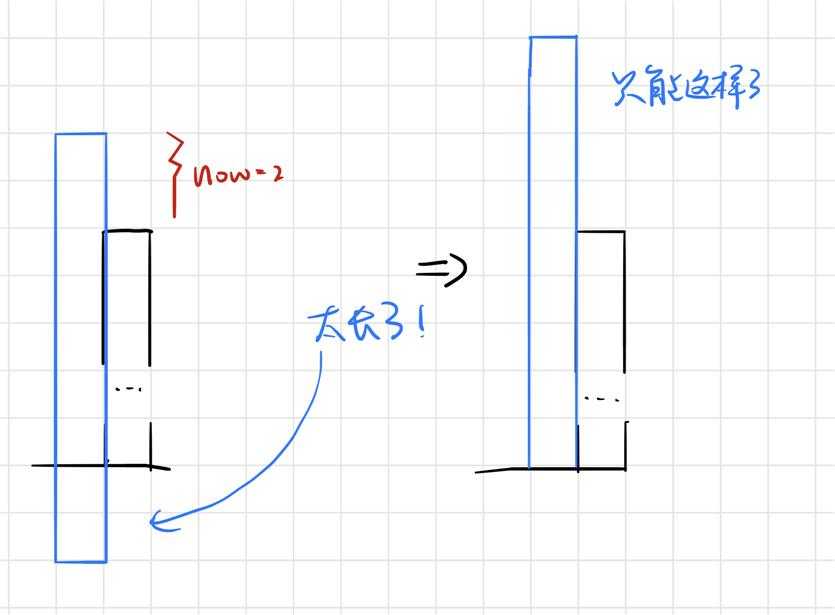
如果当前区间的长度太长了的话,为了不越界就只能把1~a[i]全涂上,这样露出的部分肯定大于now,以后的情况只能听天由命了,起码能保证现在是合法的。执行b[i]=1; top=a[i];
#include <bits/stdc++.h> using namespace std; int n,m,a[100005],b[100005]; int main() { cin>>n>>m; int i; for(i=1;i<=m;i++)scanf("%d",&a[i]);//每种颜色对应的长度实际上是a[i] bool flag=1; int top=0; for(i=m;i>=1;i--) { //后面的会覆盖前面的 所以先排后面的,然后要保证前面的至少要露出一个单位不被后面的挡住 if(i==m) { top=a[i]; b[i]=1; continue; } int res=i; if(n-top<res)//res比较多 必然有颜色会被挡住 { flag=0; break; } else//颜色少而空白多,尽可能填:看当前颜色能否弥补成恰好的情况。如果不能的话则尽可能弥补/放到最底端 { int now=n-top-(res-1);//需要弥补使分配给当前颜色的长度 if((now+top-a[i]+1)>=1&&(now+top-a[i]+1)<=top)//能恰好弥补 { b[i]=(now+top-a[i]+1); top+=now; } else if((now+top-a[i]+1)<1) { b[i]=1; top=a[i]; } else //当前颜色长度不够 尽可能弥补 { b[i]=top+1; top+=a[i]; } } if(top>n) { flag=0; break; } } if(top<n)flag=0; if(!flag)cout<<-1<<endl; else { for(i=1;i<=m;i++) { printf("%d ",b[i]); } } return 0; }
然后就是当前区间太短了,无法满足露出now长度的要求,这样只能尽可能地覆盖,至于以后也是听天由命。执行b[i]=top+1; top+=a[i];
遍历时随时检查,如果确定了不能满足的话直接退出即可。
Codeforces Round #631 (Div. 2) C. Dreamoon Likes Coloring(贪心好题/意识流题解)
标签:print 分类 ssis i+1 操作 ons 固定 opera other
原文地址:https://www.cnblogs.com/lipoicyclic/p/12635613.html