标签:namespace const pac row 01背包 完全背包 删除 mes 复杂度
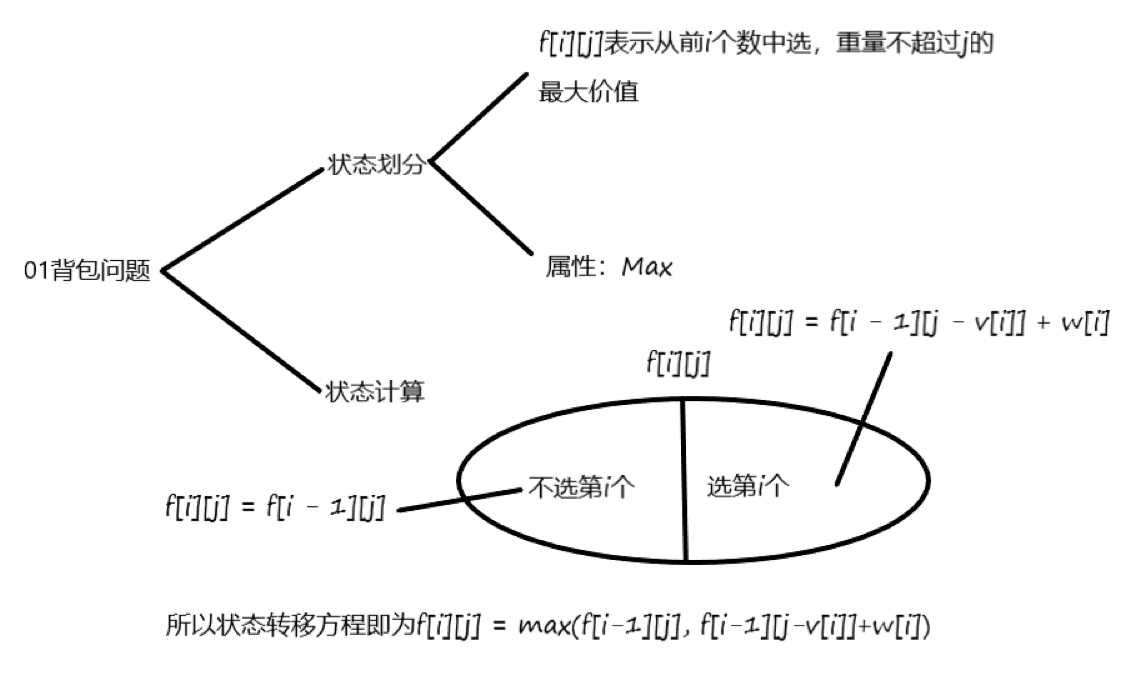
而我们所求的结果就是$f[n][m]$。
1 #include <iostream> 2 #include <algorithm> 3 4 using namespace std; 5 6 7 const int N = 1010; 8 int v[N], w[N]; 9 int f[N][N]; 10 int n, m; 11 12 int main(){ 13 cin >> n >> m; 14 for(int i = 1 ; i <= n ; i ++)cin >> v[i] >> w[i]; 15 16 for(int i = 1 ; i <= n ; i ++) 17 for(int j = 0 ; j <= m ; j ++) 18 { 19 f[i][j] = f[i - 1][j]; 20 if(j >= v[i])f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); 21 } 22 cout << f[n][m] << endl; 23 return 0; 24 }
优化:
由于计算$f[i][j]$,即第$i$层的时候,只用到了$i-1$层的状态,所以是可以考虑优化掉一维的数组的。当拿掉一维后,$f[i][j] = f[i-1][j] \leftrightarrow f[j] = f[j]$,式子等价,直接删除。而对于$f[i][j] = max(f[i][j], f[i-1][j-v[i]]+w[i])$来说,因为目前要计算的状态是由上一层的当前状态$A$和上一层的当前状态的前一个状态$B$转移过来。所以在计算当前状态的时候,$B$已经被更新成了当前层的状态,即$f[i-1][j-v[i]]$已经变成了$f[i][j-v[i]]$,所以是不能按顺序进行更新的,而当$j$从大到小逆序枚举时,该式子就可以直接去掉一维,依旧是等价的。
1 int main(){ 2 cin >> n >> m; 3 for(int i = 1 ; i <= n ; i ++)cin >> v[i] >> w[i]; 4 5 for(int i = 1 ; i <= n ; i ++) 6 for(int j = m ; j >= v[i] ; j --) 7 f[j] = max(f[j], f[j - v[i]] + w[i]); 8 cout << f[m] << endl; 9 return 0; 10 }
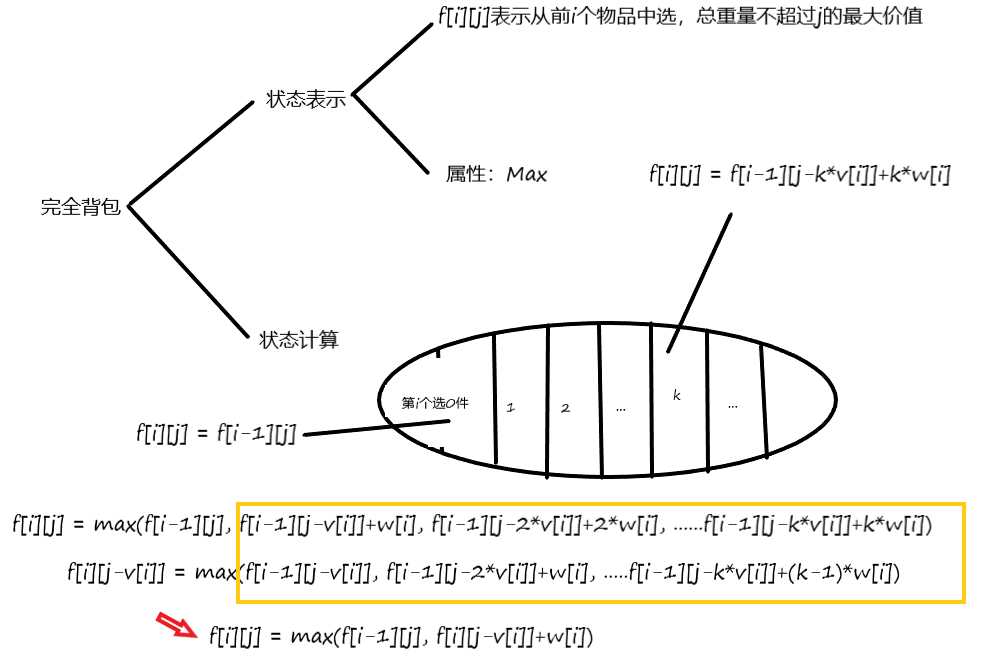
如同$01$背包,但是注意的是当前需要计算的状态是由上一层的当前状态$A$和当前层的当前状态的前一个状态$B$转移过来,而当$j$按顺序枚举时,在计算当前状态的时候,$B$已经被算出,可以直接转移,所以在去掉一维数组后,$j$是按顺序枚举的。
1 #include <iostream> 2 #include <algorithm> 3 4 using namespace std; 5 6 const int N = 1010; 7 int f[N], w[N], v[N]; 8 int n, m; 9 10 int main(){ 11 cin >> n >> m; 12 for(int i = 1 ; i <= n ; i ++)cin >> v[i] >> w[i]; 13 14 for(int i = 1 ; i <= n ; i ++) 15 for(int j = v[i] ; j <= m ; j ++) 16 f[j] = max(f[j], f[j - v[i]] + w[i]); 17 18 cout << f[m] << endl; 19 return 0; 20 }
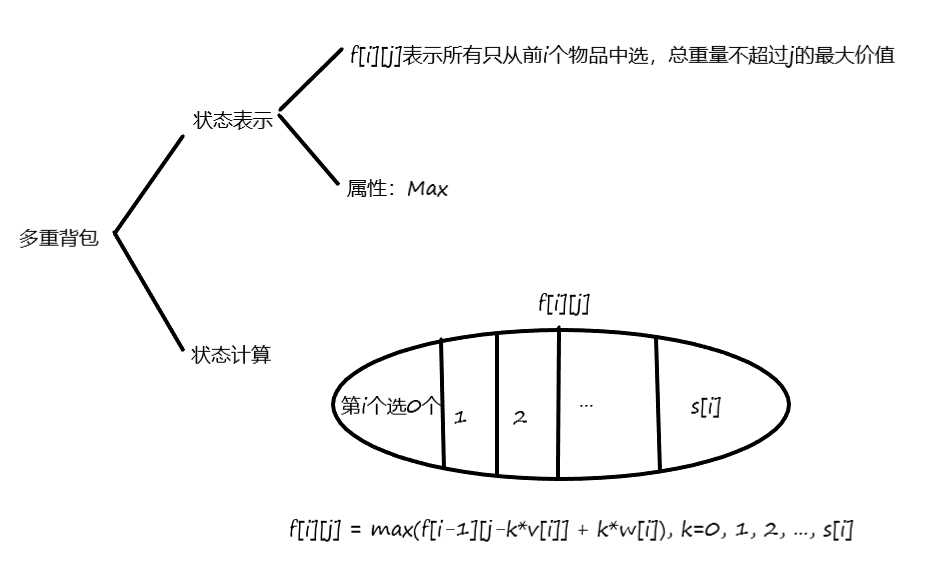
朴素版本:时间复杂度$O(NMS)$
1 #include <iostream> 2 #include <algorithm> 3 4 using namespace std; 5 6 const int N = 110; 7 8 int n, m; 9 int v[N], w[N], s[N]; 10 int f[N][N]; 11 12 int main() 13 { 14 cin >> n >> m; 15 16 for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i] >> s[i]; 17 18 for (int i = 1; i <= n; i ++ ) 19 for (int j = 0; j <= m; j ++ ) 20 for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ ) 21 f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k); 22 23 cout << f[n][m] << endl; 24 return 0; 25 }
优化:

二进制优化:
枚举一个数字的时候,例如枚举$37$这个数字,可以将其分为$1,2,4,8,16,32, 5$。我们可以用这$7$个数字,拼凑出$0$到$36$中的任何一个数。所以用这种方法枚举会比一个个枚举更加高效。
这样,就能将$s$的循环从$O(n)$优化为$O(logn)$的复杂度。
时间复杂度$O(NMlogS)$
1 #include <iostream> 2 #include <algorithm> 3 4 using namespace std; 5 6 const int N = 12010, M = 2010; 7 8 int n, m; 9 int v[N], w[N]; 10 int f[M]; 11 12 int main() 13 { 14 cin >> n >> m; 15 16 int cnt = 0; 17 for (int i = 1; i <= n; i ++ ) 18 { 19 int a, b, s; 20 cin >> a >> b >> s; 21 int k = 1; 22 while (k <= s) 23 { 24 v[++ cnt] = a * k; 25 w[cnt] = b * k; 26 s -= k; 27 k *= 2; 28 } 29 if (s > 0) 30 { 31 v[++ cnt] = a * s; 32 w[cnt] = b * s; 33 } 34 } 35 36 //跑一遍01背包 37 for (int i = 1; i <= cnt; i ++ ) 38 for (int j = m; j >= v[i]; j -- ) 39 f[j] = max(f[j], f[j - v[i]] + w[i]); 40 41 cout << f[m] << endl; 42 43 return 0; 44 }
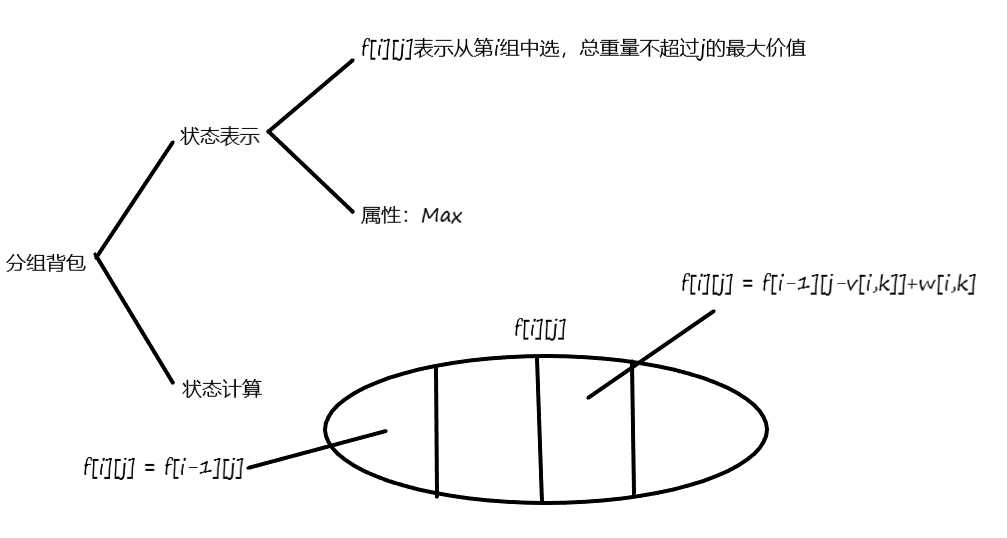
1 #include <iostream> 2 #include <algorithm> 3 4 using namespace std; 5 6 const int N = 110; 7 8 int n, m; 9 int v[N][N], w[N][N], s[N]; 10 int f[N]; 11 12 int main() 13 { 14 cin >> n >> m; 15 16 for (int i = 1; i <= n; i ++ ) 17 { 18 cin >> s[i]; 19 for (int j = 0; j < s[i]; j ++ ) 20 cin >> v[i][j] >> w[i][j]; 21 } 22 23 for (int i = 1; i <= n; i ++ ) 24 for (int j = m; j >= 0; j -- ) 25 for (int k = 0; k < s[i]; k ++ ) 26 if (v[i][k] <= j) 27 f[j] = max(f[j], f[j - v[i][k]] + w[i][k]); 28 29 cout << f[m] << endl; 30 31 return 0; 32 }
混合背包问题其实就将$01$背包,完全背包,多重背包问题混合起来,关键在于物品的个数$s$。如果$s$为$14,那么当前就用$01$背包更新;如果$s$有无限个,那么当前就用完全背包更新;如果$s$有限个且大于$1$,那么当前就用多重背包更新。其中$01$背包属于多重背包的特殊情况,可以合并起来。
1 #include <iostream> 2 #include <algorithm> 3 4 using namespace std; 5 6 const int N = 1010; 7 8 int n, m; 9 int f[N]; 10 11 int main() 12 { 13 cin >> n >> m; 14 15 for (int i = 0; i < n; i ++ ) 16 { 17 int v, w, s; 18 cin >> v >> w >> s; 19 if (!s) 20 { 21 for (int j = v; j <= m; j ++ ) 22 f[j] = max(f[j], f[j - v] + w); 23 } 24 else 25 { 26 if (s == -1) s = 1; 27 for (int k = 1; k <= s; k *= 2) 28 { 29 for (int j = m; j >= k * v; j -- ) 30 f[j] = max(f[j], f[j - k * v] + k * w); 31 s -= k; 32 } 33 if (s) 34 { 35 for (int j = m; j >= s * v; j -- ) 36 f[j] = max(f[j], f[j - s * v] + s * w); 37 } 38 } 39 } 40 41 cout << f[m] << endl; 42 43 return 0; 44 }
标签:namespace const pac row 01背包 完全背包 删除 mes 复杂度
原文地址:https://www.cnblogs.com/1-0001/p/12638144.html