标签:解决方法 完全 syn under 针对 概率分布 健康 分类器 取数据
本文详细介绍了类别不平衡问题,目录:
类别不平衡(class-imbalance),也叫数据倾斜,数据不平衡,就是指分类任务中不同类别的训练样例数目差别很大的情况。在现实的分类学习任务中,我们经常会遇到类别不平衡,例如交易欺诈、广告点击率预测、病毒脚本判断等;或者在通过拆分法解决多分类问题时,即使原始问题中不同类别的训练样例数目相当,在使用OvR(One vs. Rest)、MvM(Many vs. Many)策略后产生的二分类任务仍然可能出现类别不平衡现象。而标准机器学习算法通常假设不同类别的样本数量大致相似,所以类别不平衡现象会导致学习算法效果大打折扣。因此有必要了解类别不平衡时处理的基本方法。
通常情况下,类别不平衡程度越高,数据集的分类难度越大,但情况并非总是如此。下面列了几种类别不平衡的情况:
第1种是最好的情况,在这些数据集上直接使用合适的模型(如SVM,Decision Tree等对类别不平衡问题不敏感的模型)通常也能得到很好的分类结果。所以从这种情况来看,类别不平衡本身并不是分类困难的来源,下面几种情况才是。
第2种情况又被称为small disjuncts问题。它导致分类困难的原因很直观:在同样的特征空间中,相比于只有一个cluster的简单少数类分布,具有多个子概念的少数类分布需要模型给出更复杂的决策边界来获得良好的预测。在模型复杂度不变的情况下,分类性能会因子概念个数的增多而变差。因此该问题的解决办法也较为简单:上更大容量的模型(DL: 更宽,更深,更强)。
第3和第4种情况表现了类似的困难,即部分或大部分少数类样本嵌入到多数类样本密集的区域,导致边界模糊,分类困难,这种困难程度随着类别不平衡的增大而进一步加剧。
第5种情况就不用说了,噪声啥时候都很讨厌,少数类的噪声更是雪上加霜。
下图给出一个直观的可视化来帮助理解类别不平衡比/类别分布重叠之间的关系:即使不平衡比相同,类别重叠/不重叠的数据集也会表现出极其不同的分类难度。深蓝色的点代表它们可以被模型很好地分类,而深红色的样本点代表模型完全无法正确分类这些数据点。数据硬度指分类器训练完成后输出概率与ground truth label的残差(i.e., |F(x)-y|)。
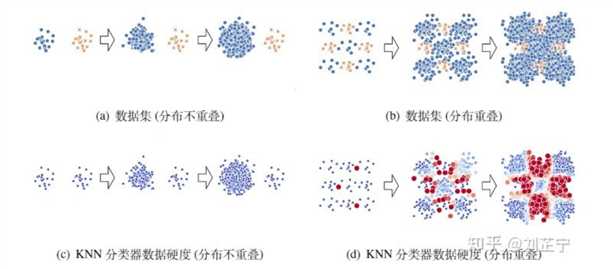
在图(a)中,数据集是用两个不重叠的的二维高斯分布生成的,来代表情况1。我们可以观察到不平衡比的增长并不会影响分类该数据集的难度(图(c))。而在图(b)中,数据集由两个相互重叠的二维高斯混合分布生成,来代表情况2、3、4。可以看出,随着不平衡比的增加,它从一个相对简单的分类任务变成了一个极其困难的任务(图(d))。
另外,在实际的工业应用当中,这些难度因素还会与其他实际问题一同出现,如特征中的缺失值,巨大的数据集规模等。
每种解决方法都有其适用范围,需要因地制宜。甚至有时候根本就不需要专门处理,比如这两种情况:
但是,如果我们对于召回有特别大的需求,也就是说我们更关心正样本,那么这个时候如果不做任何处理就很难拿到我们所希望的结果。因此,下面介绍几种解决这个问题的方法,包括省心的方法、调整数据、调整算法和集成。
注:本文中正样本(正例)就是少数类,负样本(负例)就是多数类,欠采样同下采样,过采样同上采样。
在介绍后面三种高级方法之前,先介绍几种朴实无华但很省心的方法。
主动收集数据
针对少量样本数据,可以尽可能去扩大这些少量样本的数据集,或者尽可能去增加他们特有的特征来丰富数据的多样性(尽量转化成情况1)。譬如,如果是一个情感分析项目,在分析数据比例时发现负样本(消极情感)的样本数量较少,那么我们可以尽可能在网站中搜集更多的负样本数量,或者花钱去买,毕竟数据少了会带来很多潜在的问题。
将任务转换成异常检测问题
如果少数类样本太少,少数类的结构可能并不能被少数类样本的分布很好地表示,那么用平衡数据或调整算法的方法不一定有效。如果这些少数类样本在特征空间中再分布的比较散,情况会更加糟糕。这时候不如将其转换为无监督的异常检测算法,不用过多的去考虑将数据转换为平衡问题来解决。
调整权重
可以简单的设置损失函数的权重,让模型增加对多数类的惩罚,更多的关注少数类。在python的scikit-learn中我们可以使用class_weight参数来设置权重。
另外,调整权重方法也适合于这种情况:不同类型的错误所造成的后果不同。例如在医疗诊断中,错误地把健康人诊断为患者可能会带来进一步检查的麻烦,但是错误地把患者诊断为健康人,则可能会丧失了拯救生命的最佳时机;再如,门禁系统错误地把可通行人员拦在门外,将使得用户体验不佳,但错误地把陌生人放进门内,则会造成严重的安全事故;在信用卡盗用检查中,将正常使用误认为是盗用,可能会使用户体验不佳,但是将盗用误认为是正常使用,会使用户承受巨大的损失。为了权衡不同类型错误所造成的不同损失,可为错误赋予“非均等代价”(unequal cost)。
阈值调整(threshold moving)
直接基于原始训练集进行学习,但在用训练好的分类器进行预测时,将原本默认为0.5的阈值调整到 \(\frac{|P|}{(|P|+|N|)}\)即可。(大部分是负样本,因此分类器倾向于给出较低的分数)
调整数据的方法(也称为重采样方法)是不平衡学习领域发展最早、影响力最大、使用最广泛的一类方法,关注于通过修改训练数据集以使得标准学习算法也能在其上有效训练。根据实现方式的不同,可被进一步分类为:
由于随机欠采样可能会丢失含有重要信息的样本,随机过采样可能会招致严重的过拟合(简单的复制少数类的样本),引入无意义的甚至有害的新样本(粗暴地合成少数类样本),因此发展了一系列更高级的方法,试图根据数据的分布信息来在进行重采样的同时保持原有的数据结构。
注意:在重采样过程中,要尽可能的保持训练样本和测试样本的概率分布是一致的。如果违背了独立同分布的假设,很可能会产生不好的效果。
下面介绍三种典型欠采样方法,其思想是,类别间的边缘可能增大分类难度,通过去除边缘中的多数类样本可以使得类别间margin更大,便于分类。
Edited Nearest Neighbor (ENN)
针对那些多数类的样本,如果它的大部分k近邻样本都跟它本身的类别不一样,就说明它处于类别边缘交界处,我们就把它删除。
Repeated Edited Nearest Neighbor(RENN)
这个方法就是不断的重复上述的删除过程,直到无法再删除为止。
Tomek Link Removal
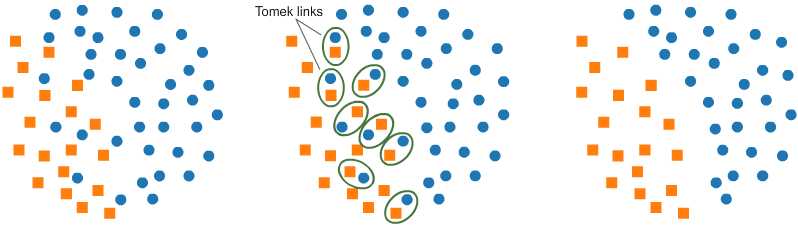
如果有两个不同类别的样本,它们的最近邻都是对方,也就是A的最近邻是B,B的最近邻是A,那么A,B就是Tomek link,我们要做的就是将所有Tomek link都删除掉。那么一个删除Tomek link的方法就是,将组成Tomek link的两个样本,如果有一个属于多数类样本,就将该多数类样本删除掉。这样我们可以发现正负样本就分得更开了。如下图所示。
SMOTE(Synthetic Minority Oversampling,合成少数类过采样)
SMOTE是对随机过采样方法的一个改进算法,通过对少数类样本进行插值来产生更多的少数类样本。基本思想是针对每个少数类样本,从它的k近邻中随机选择一个样本 (该样本也是少数类中的一个),然后在两者之间的连线上随机选择一点作为新合成的少数类样本。
SMOTE会随机选取少数类样本用以合成新样本,而不考虑周边样本的情况,这样容易带来两个问题:
总的来说我们希望新合成的少数类样本能处于两个类别的边界附近,这样往往能提供足够的信息用以分类。这就是下面的 Borderline SMOTE 算法要做的事情。
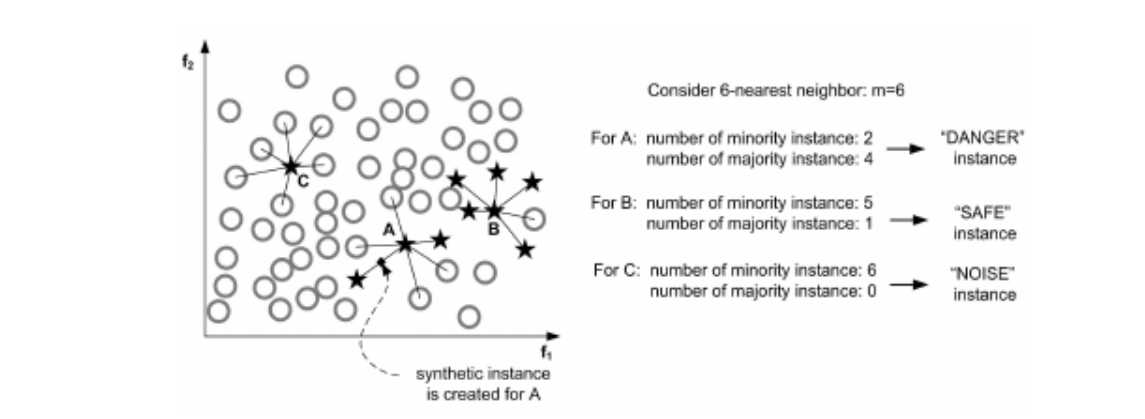
Borderline SMOTE
过程:
实际貌似并没有带来多少效果提升,可能是对数据分布掺水太多?
优点:
缺点:
调整算法的方法主要是修改现有的标准机器学习算法以修正他们对多数类的偏好。在这类方法中最流行的分支是代价敏感学习(cost-sensitive learning)。
代价敏感学习是对调整权值方法的扩展,调整权重的方法通常用在二分类中,但是代价敏感学习把这种思想进一步扩展,可以设置代价矩阵用于多分类,也可以用代价矩阵对标准算法进行改造,使其适应不平衡数据的学习,比如针对决策树,可以将代价矩阵代入到决策阈值选择、分裂标准、剪枝这三个方面。
代价敏感学习的优点:
代价敏感学习的缺点:
人多力量大,总有一款集成方法适合你。这里主要介绍两种:EasyEnsemble算法和BalanceCascade算法。
EasyEnsemble算法
类似Bagging的方法。每次从负例N(多数类)中有放回抽取出一个子集N‘,大小同正例P(少数类);将每个子集N‘与P联合起来训练生成多个基分类器;最终将这些基分类器组合形成一个集成学习系统(通过加权平均或者算术平均)。
BalanceCascade算法
基于Adaboost,将Adaboost作为基分类器。在每一轮训练时都使用与正例P数量相等的训练集N‘,训练出一个Adaboost基分类器;然后使用该分类器对负例集合N进行预测,通过控制分类阈值来控制假正例率FPR为f,将N中所有判断正确的负例删除;重复迭代T次。(注意:每一次删除后留下的比例为f,则迭代T-1次后剩下的负例数量为|N|*f^(T-1),即等于正例个数|P|,然后再迭代最后一次。)
优点:
缺点:
由于类别不平衡,而且我们也比较关心少数类的正样本,因此:
注意:
由于三维以上的特征空间难以可视化,所以通常难以直观地针对数据本身的特点去选择合适的方法,但是各种方法都有其适用的范围,这是难点所在。如果非要推荐一款又高级又好用的方法,那就先试试 随机降采样 + Bagging。
Reference
标签:解决方法 完全 syn under 针对 概率分布 健康 分类器 取数据
原文地址:https://www.cnblogs.com/inchbyinch/p/12642760.html