标签:证明 回归 image 方法 原则 不可 交点 情况 标记
题意: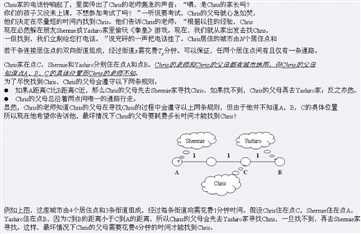
其实就是找到AB+min(AC,BC)的最大值
分析:刚看到这道题,很容易往AB为树的直径方向上去想,C就可以遍历每个点,最后求出对于每个点为C时的最大值
那AB到底是不是树的直径或者为什么AB是树的直径呢?
(下面是我自己yy的证明方法,可能有不严谨甚至有错误,望指正)
所有的ABC都可以用这个模型来代替
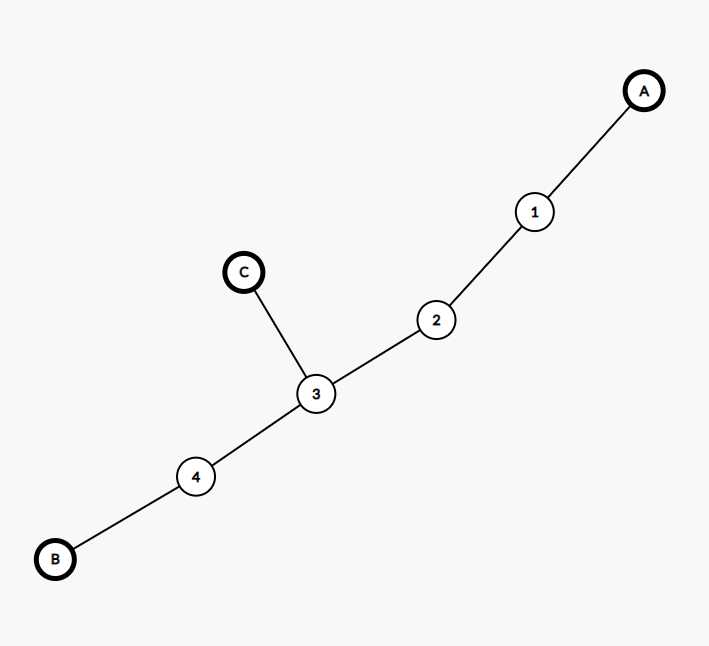
也就是在AB这条链上会长出C这样一条分支
我把AB与C链的交点叫做D
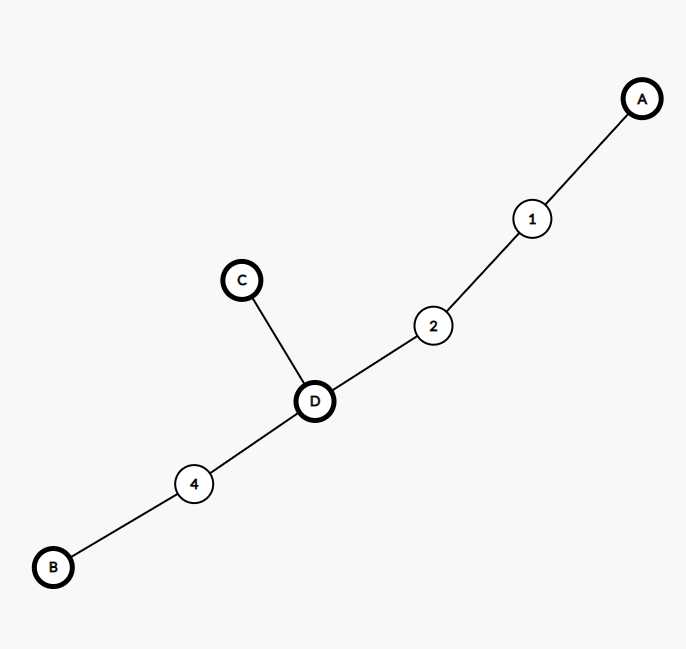
对于BD CD AD 这三段,将其中较长的两条作为“AB链”,最短那条作为“C链”会更优
证明:设AD=a,BD=b,CD=c
若以ab为主链,结果就是 a+b+c+min(a,b)
若以ac为主链,结果就是 a+b+c+min(a,c)
若以bc为主链,结果就是 a+b+c+min(b,c)
显然拿最大的两条作为主链会更优,我们假设AD>=BD>=CD
那么我们就可以获得一个建立在这个基础上的结论:CD<=BD<=AD<=(AD+BD)/2=AB/2
也就是CD<=AB/2,还有结果AD+BD+CD+BD<=2AB
然后就可以正式开始这道题的证明了:
如果我们设AB为当前树的直径,如果A‘B‘作为直径更优,分两类讨论
如果A‘B‘与AB不相交,那么A‘B‘<AB/2,那以A‘B‘为主链的结果<=2A‘B‘<AB
而以AB为主链的结果显然大于AB
所以不成立
如果A‘B‘与AB相交,这里还有重合与不重合的讨论,我们先考虑不重合的,令他们的交点为E(这里也遵循AE>=BE的原则)
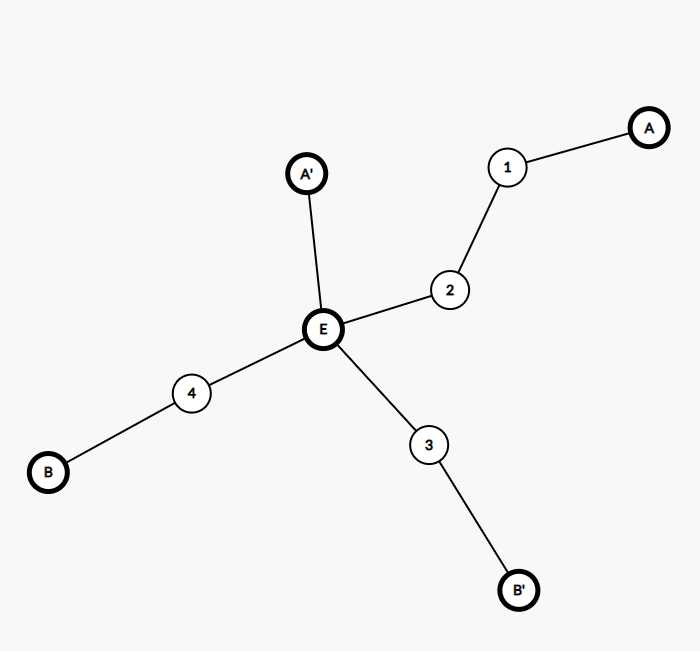
能得到EB‘,A‘E<=BE,如果EB‘,A‘E>BE那E‘B,A‘E就会代替BE成为最长链,那就会变成重合的情况了
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!注意 A‘B‘链中的D‘点永远不可能在AB链中,这条规则在任何条件下都适用,如果这里没想明白,后面很可能自己证着证着就因为画图改变初始规则导致证不下去(亲身体会)
!!!!因为如果D‘点与D点重合,A‘D比AD 要短,B‘D比BD 要短,A‘B‘永远不可能超越AB,如果A‘D比AD长或者B‘D比BD 长的话显然AB就不是最长链了,A‘B或AB‘就成最长链了
!!!!(这里我认为是我证这个路上最大的绊脚石)
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
在我现在无论C‘点在哪,我的C点都去与C‘点重合,再根据我们命名的规则把D,D‘给标记出来
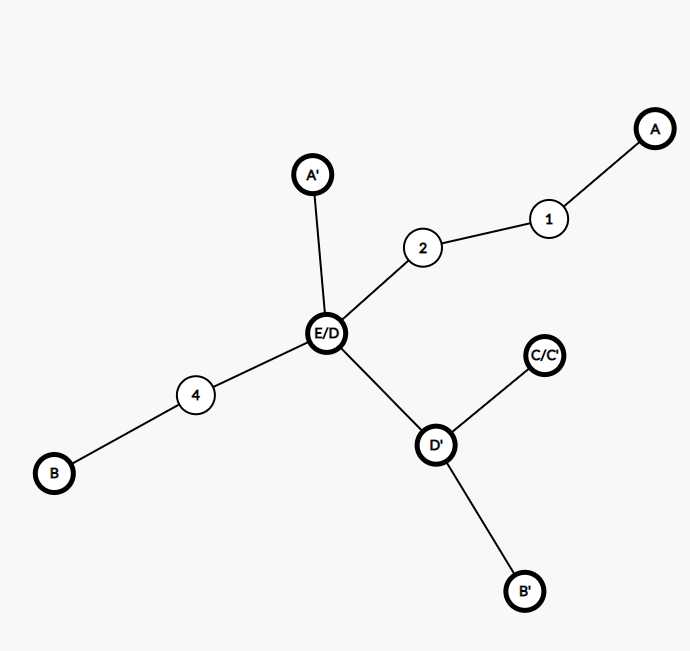
以A‘B‘为主链的结果就是A‘B‘+C‘D‘+B‘D‘=A‘E+ED‘+D‘B‘+C‘D‘+B‘D‘
以AB为主链的结果就是AB+CD+BD=AE+EB+CD‘+D‘E+BE
两边作差就会发现
AB-A‘B‘=(AE+BE*2)-(A‘E+B‘D*2)
而我们的B‘D‘<=B‘D<=BD,A‘E<=AE
所以A‘B‘<=AB
然后就是AB与A‘B‘重合的可能
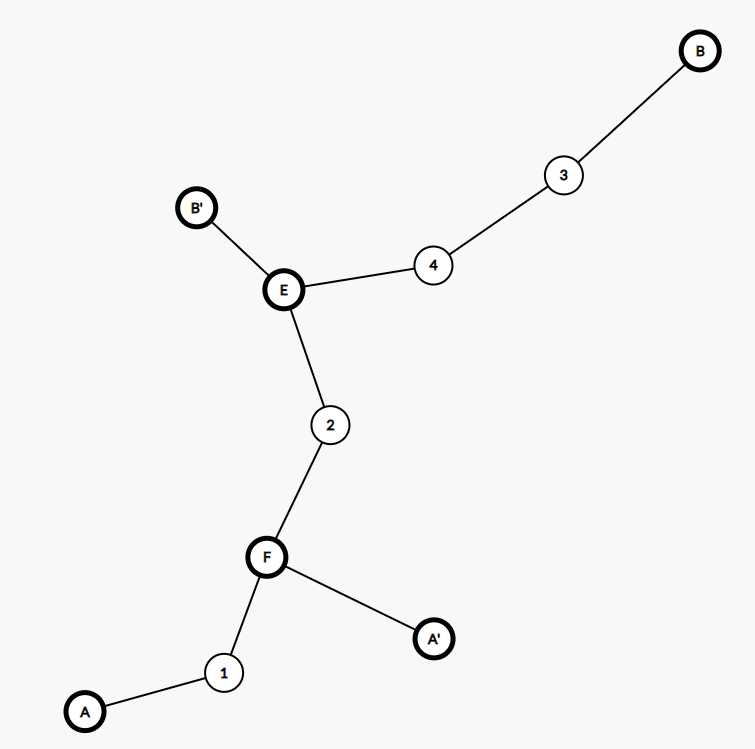
这里还是无论C‘点在哪,C点都与他重合
这里的证明方法其实跟AB与A‘B‘相交的证明方法类似,这里就不再证一遍了
!!!!!唯一需要再强调一遍的就是一定不要把A‘与A 或者B‘与B标反了
!!!!!别突然想到一组数据,自己手玩发现不符合这个规律,结果是A‘D比AD都要长了
最后再回归到这个题上
求出最长链之后,处理出最长链端点到每个节点的距离,把每个节点当做C计算一遍,取最大值就可以了
代码:

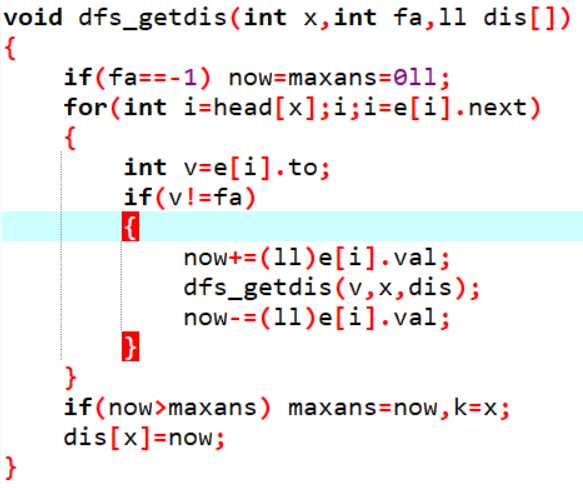
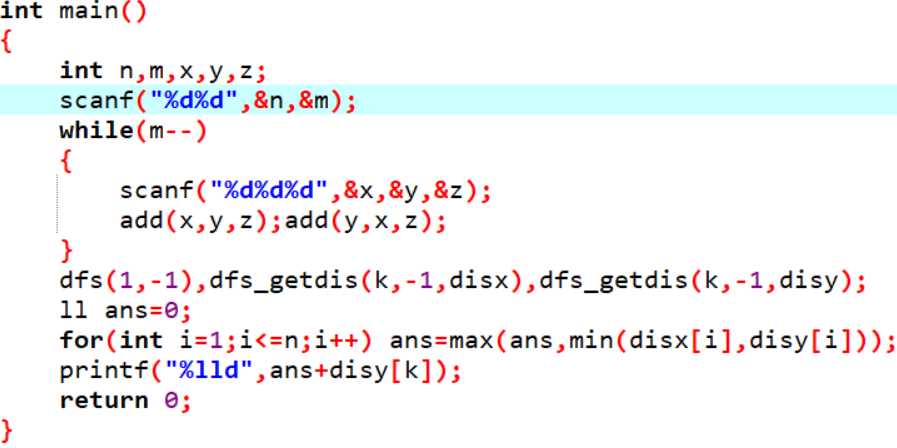
ps:我主函数写的稍微有些图方便,比如都是k,可能理解起来比较麻烦,不过这题证出是直径之后就很简单了,稍微看一下代码的流程绝对能写出来,不需要理解我这种写法
标签:证明 回归 image 方法 原则 不可 交点 情况 标记
原文地址:https://www.cnblogs.com/lin4xu/p/12665962.html