标签:考证 均值 设定 image city 金融 anti mat 相对
小声逼逼一句,学长有毒吧~~让我进金融的东东,我懂个锤子??
金融资产的波动是一个非常重要的概念,它与资产的风险直接相关,因此对资产的波动模式进行建模是量化投资中的一个重要课题。一般来讲,波动建模有以下量化投资方向的应用:
期权定价:波动率是影响期权价值的重要因素;
风险度量和管理:在VaR的计算中波动率是主要影响因素,根据波动率决定交易策略的杠杆;
资产价格预测和模拟:通过Garch簇模型对资产价格的时间序列进行预测和模拟;
调仓:盯住波动率的调仓策略,如一个tracing指数的策略;
作为交易标的:在VIX、ETF以及远期中波动率作为标的可以直接交易。
上面的几行确实没明白,正确性有待考证
金融时间序列分析的核心是找到资产收益率序列的自相关性,并利用它。川流不息
在讲Garch模型之前,我们必须对同方差和异方差的概念进行回顾。在时间序列的弱平稳条件中二阶矩是一个不变的、与时间无关的常数。在理想条件下,如果这个假设是成立的,那么金融时间序列的预测将会变得非常简单,采用ARIMA等线性模型就能做不错的预测。然而采用Ariam等模型对金融事件序列建模效果是非常差的,原因就在于金融事件序列的异方差性。这种非平稳性无法用简单的差分去消除,其根本原因在于其二阶矩随时间t变化而变化。扯扯金融
这里说的方差是回报率(收益率)
简单的理解就是说对于普通的时间序列,一般采用取n差分或者取对数或者滞后,就可以使时间序列平稳,这个的前提是方差不随时间变化也就是同方差(此时方差是个常数,因为是不随时间变化的),这个时候可以使用ARIMA进行预测了。
但是金融时间序列的方差是随着时间变化而变化的,方差不在是一个常数了。
异方差描述的是金融时间序列大的趋势,时间跨度相对较长。金融时间序列的另一个特征是波动聚集,它是在小时间尺度下的波动特性(可以理解为小尺度下的异方差表现)。一般来讲,金融时间序列的波动具有大波动接着大波动,小波动接着小波动的特征,即波峰和波谷具有连续性。在高波动的时候,人们情绪高涨市场的势能不断积累,于是会转化成更大的波动;在低波动的时候,人们对市场的兴趣越来越低,市场逐渐会成为一摊死水。此外,金融事件序列存在波动的不对称性,在上涨时候的波动率会小于下跌时候的波动率。
Garch模型作为现代的金融事件序列模型,是基于波动聚集这个特性建模的。波动聚集告诉我们当前的波动率是和过去的波动率存在一定的关系,方差的概念也相应的扩展到条件方差,所谓条件反差指的是过去时刻信息已知的方差。Garch模型认为本期的条件方差是过去N期条件方差和序列平方的线性组合,而序列是本期条件方差和白噪声的乘积。
以 2012 年 1 月 1 日到 2019 年 7 月 31 日上证指数日频对数收益率为例,假设使用 ARMA(3, 2) 对其建模,并考察其残差。下图展示了残差时序以及它的 ACF 和 Partial ACF(PACF)。
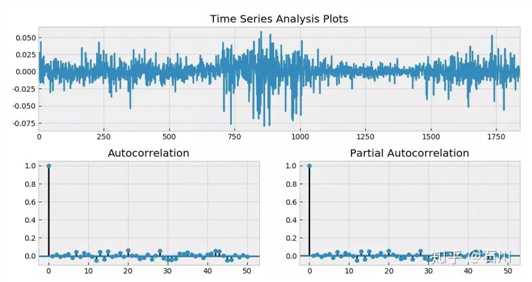
从 ACF 和 PACF 上不难看出,在很多 lags 上,自相关系数是超过 95% 的置信区间的;而从最上面一副图中也能明显看出收益率序列的一大特征 —— 波动率聚类。如果把残差取平方,并再次作图,上述波动率聚类则会变得更加直观。它在数学上被称为条件异方差(conditional heteroskedasticity)。
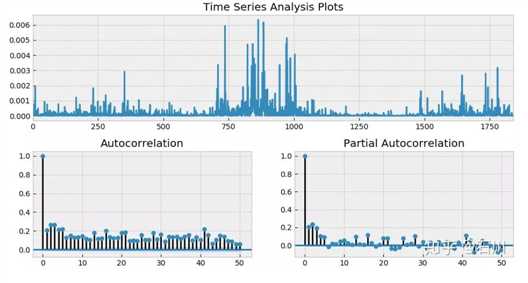
上述结果意味着,仅使用 ARMA 对收益率序列建模是不够的,它对条件异方差无能为力。为了解决这个问题需要对波动率建模,即使用 Generalized Autoregressive Conditional Heteroskedasticity(GARCH)模型。
在采用ARMA、ARIMA模型建模后如发现残差的平方具有自相关性,那么说明有高阶的时间序列特征未被捕捉到(仍在残差中),采用ARMA或者ARIMA模型建模是不合适的,需要采用GARCH模型建模。采用Garch建模后的序列残差即为真正的白噪声,其平方不再具有自相关性。可以证明的是,序列的Garch(p,q)模型等价于序列平方的ARMA(max(p,q),p)模型
邵昱:就证券而言,收益率是指是所有现金流的净现值为0的折现率,回报率就是利息收入与投资的比例
噗,介绍一堆公式
\(r_{t}=c_{1}+\sum_{i=1}^{R} \phi_{i} r_{t-i}+\sum_{j=1}^{M} \phi_{j} \epsilon_{t-j}+\epsilon_{t} \cdots \cdots(1)\) 均值方程
\(\epsilon_{t}=u_{t} \sqrt{h_{t} \cdots \cdots}(2)\) 分布假设
\(h_{t}=k+\sum_{i=1}^{q} G_{i} h_{t-i}+\sum_{j=1}^{p} A_{i} \epsilon_{t-i}^{2} \cdots \cdots(3)\) 方差方程
对三个部分进行适当的变形后可以形成egarch模型,egarch-ged模型,egarch-t模型,Igarch模型,garch-m模型和Qgarch模型等。因此,设定模型形式就是分别设定均值方程、方差方程和分布。rugarch包的优越之处正在于这里。ugarchspec函数的参数也被分解为为三个主要部分,分别是variance.model,对应式(3),mean.model,对应式(1),distribution.model对应式(2)中的\(\epsilon\)。用户通过对三个部分的参数的分别设定从而构造出自己想用的模型。蘭亭客
标签:考证 均值 设定 image city 金融 anti mat 相对
原文地址:https://www.cnblogs.com/gaowenxingxing/p/12678722.html