平衡二叉树

标签：code   左右子树   strong   斐波那契   str   旋转   斐波那契数列   补充   树的高度   

AVL树说明：

    该树是一种高度平衡的二叉搜索树，该树中的每一个结点左右子树的高度至多相差1。

    AVL树本身也是一个二叉搜索树。

斐波那契数列：

    1、1、2、3、5、8、13、21、34、……

    其递推式定义为：F(1) = 1, F(2) = 1, F(n) = F(n-1) + F(n-2) (n>=3)

    即斐波那契数列的第1、第2项都为1，然后后面的每一项都是前两项之和。

平衡二叉树最少结点计算：

    完全二叉树是平衡二叉树最“完全”的状态。

    那满足平衡二叉树的最不完全的状态，即结点最少的状态是怎样的？

    树高度记为h，树中结点总数记为C，结点内的值代表度，则：

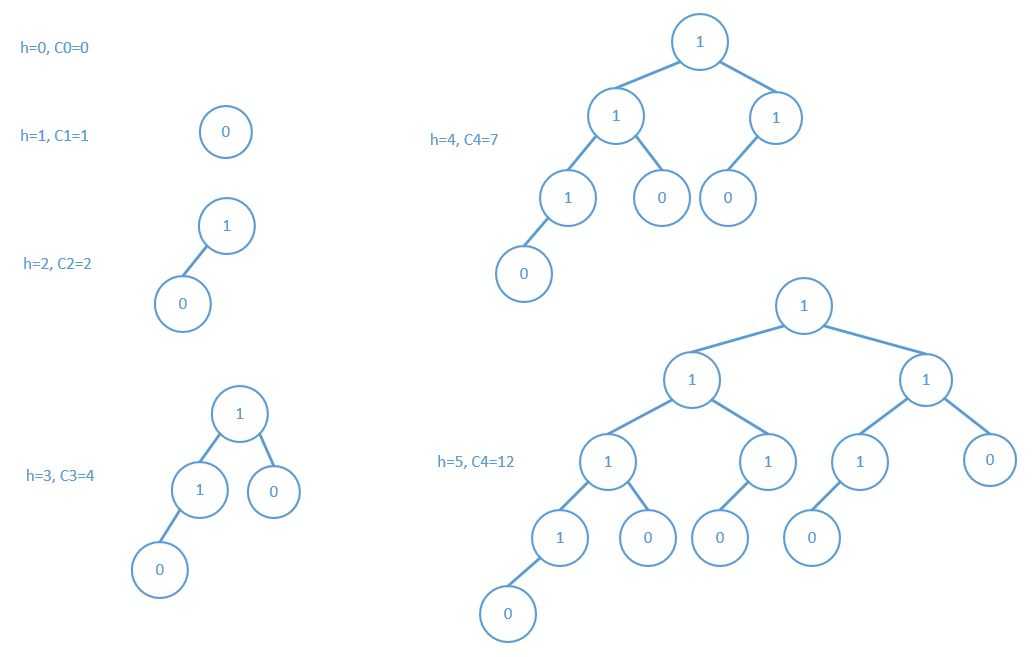
    高度为h的平衡二叉树的最少结点总数为C_h = C_h-1 + C_h-2 + 1

    和斐波那契数列对比：

     Fh 1 1 2 3  5 8  13 21 34
     Ch 1 2 4 7 12 20 33

     所以Ch = F(n+2) - 1

     如何画出上面的图：每次增加一个最左结点导致高度加1，然后需要补充一些结点，在原来树中度为0的结点下增加一个左孩子，度为1的

     结点下增加一个右孩子即可。

AVL树旋转详解

    若某节点a出现失衡，即左子树或右子树长高了，导致左右子树的高度差2，会有以下四种情况：

•  该点左子树比右子树高度高2，因为原来是平衡的，所以新结点一定是左孩子的孩子结点

       1. 在左孩子的左子树上插入结点

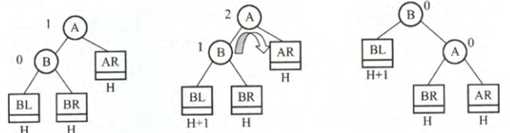
           A,B两个结点一定存在，其余抽象，插入新结点后，BL这棵树高度加1。

       2. 在左孩子的右子树上插入结点

•  该点右子树比左子树高度高2，因为原来是平衡的，所以新结点一定是右孩子的孩子结点

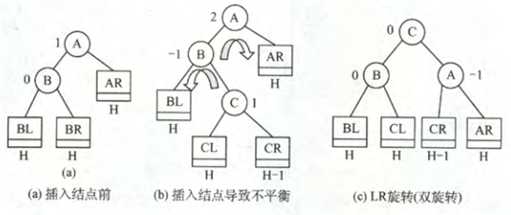
       1. 在右孩子的右子树上插入结点

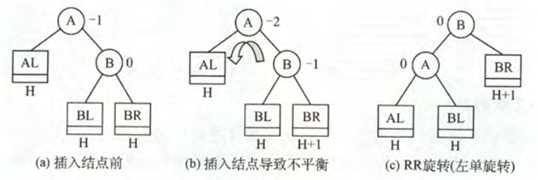
       2. 在右孩子的左子树上插入结点

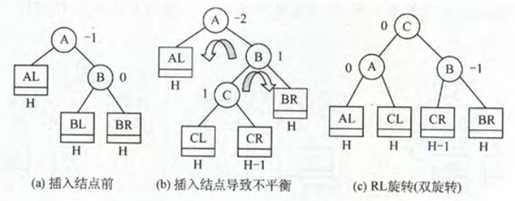
 未完待续。。。。。。

平衡二叉树

标签：code   左右子树   strong   斐波那契   str   旋转   斐波那契数列   补充   树的高度   

原文地址：https://www.cnblogs.com/yanghh/p/12683017.html