标签:power for 操作 fast slow void one 部分 ase
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
比如n=3时,2*3的矩形块有3种覆盖方法:
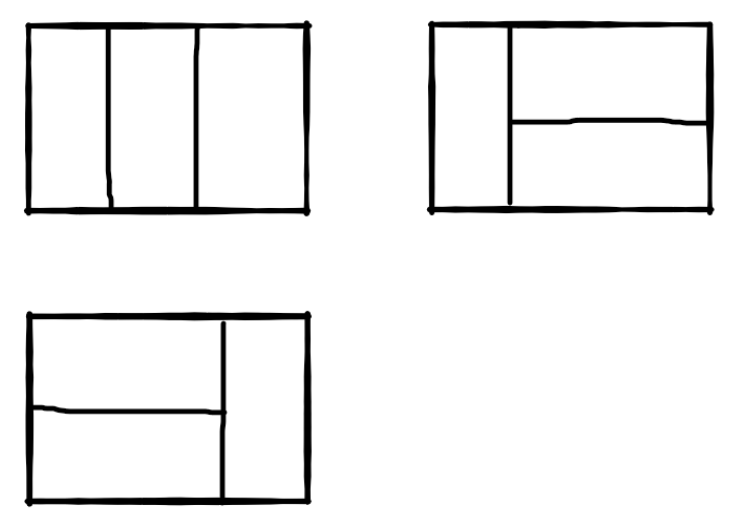
斐波那契数列的应用
第一次竖着放一块类比为走一步,第一次横着放两块类比为走两步
代码与上面的斐波那契数列类题目类似,此处不再赘述;剑指Offer系列之题6~题10。
输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
除法运算比移位运算效率低的多,应尽可能用移位运算代替乘除法。
对一个数减1,会导致其最右边的1变为0,在该1后面的0全变为1;然后将减1后的数与原数相与,则令原数最右边的1变为0。根据这个思路,与操作可以进行多少次,便是多少个1.
1.进行它的位数次 与操作 判断1:
public class Solution {
public int NumberOf1(int n) {
//正数的原码、反码、补码都相同;负数的反码是原码按位取反,补码是原码按位取反(符号位不变),最后+1
int count=0;
int flag=1;
while(flag!=0){
if((n & flag)!=0){//与运算不为0,证明n的该位是1
count++;
}
flag=flag <<1;//flag左移1位,判断n的下一位是否为1
}
return count;
}
}
2.减1后相与:
public class Solution {
public int NumberOf1(int n) {
//正数的原码、反码、补码都相同;负数的反码是原码按位取反,补码是原码按位取反(符号位不变),最后+1
int count=0;
int flag=1;
while(n!=0){
n=n&(n-1);//将最右边一位1与之后的位都变为0;5&4即0110&0100,得0100
count++;
}
return count;
}
}
给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。保证base和exponent不同时为0。
double类型的值的次方不能以普通的相乘形式求出
1.普通解法:
public class Solution {
public double Power(double base, int exponent) {
//指数为正,负
if(base==0)
return 0;
if(exponent==0){
return 1;
}
boolean flag=false;
if(exponent<0){//负指数
exponent=-exponent;
flag=true;
}
double res=1.0;
for(int i=0;i<exponent;i++){
res*=base;
}
if(flag){
res=1.0/res;
}
return res;
}
}
2.利用奇偶的n/2相乘递归:
public class Solution {
public double Power(double base, int exponent) {
//指数为正,负
if(base==0){
return 0;
}
if(exponent==0){
return 1;
}
if(exponent==1){
return base;
}
if(exponent<0){//当指数为负指数
base=1/base;
exponent=-exponent;
}
//递归
double res=Power(base,exponent >>>1 );//求出n/2
//判断奇偶,奇数:a^n=a^(n/2)*a^(n/2)*a,偶数:a^n=a^(n/2)*a^(n/2)
res*=res;
if((exponent & 1)==1){
//奇数
res*=base;
}
return res;
}
}
3.快速幂迭代:
假设求3^13 ,13的二进制位1101,3^13 = 3^8 * 3^4 * 3^1
从最右边开始与运算(利用位运算进行移位):
第一位是1,该位的值是3^1 ,则res=res*base;base=base*base(该步求出下一位的值)
第二位是0,该位的值是3^2 ,因为0所以不参与运算,只求出下一位的值,base*=base;
第三位是1,该位的值是3^4 ,则res=res*base(此时base的值是3^4);base*=base;
第四位是1,该位的值是3^8 ,则res=res*base(此时base的值是3^8);base*=base;
退出循环。
public class Solution {
public double Power(double base, int exponent) {
if(base==0)
return 0;
if(exponent==0)
return 1;
long n=exponent;
if(n<0){//当指数为负指数
base=1/base;
n=-n;
}
double res=1.0;
while(n>0){
if((n & 1)==1){//若当前位是1
res*=base;
}
base*=base;
n=n>>1;//右移一位
}
return res;
}
}
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
因为相对位置不变,所以需要稳定,都需要遍历。
1.暴力解法:
/**
* 分别统计奇数偶数的数量,然后用两个数组存储,最后再放回原数组。
*/
public class Solution {
public void reOrderArray(int [] array) {
int jCount=0;
int oCount=0;
for(int i=0;i<array.length;i++){
if((array[i] & 1)==0){
//偶数
oCount++;
}else{//奇数
jCount++;
}
}
int jArr[]=new int[jCount];
int oArr[]=new int[oCount];
jCount=0;
oCount=0;
for(int i=0;i<array.length;i++){
if ((array[i] & 1)== 1){
jArr[jCount]=array[i];
jCount++;
}else{
oArr[oCount]=array[i];
oCount++;
}
}
for(int i=0;i<jArr.length;i++){
array[i]=jArr[i];
}
for(int i=0;i<oArr.length;i++){
array[i+jArr.length]=oArr[i];
}
}
}
2.插入排序思想:
public class Solution {
public void reOrderArray(int [] array) {
//相对位置不变,稳定性
//插入排序的思想
int m = array.length;
int k = 0;//记录已经摆好位置的奇数的个数;也可以看作下一个奇数的下标
for (int i = 0; i < m; i++) {
if ((array[i] & 1) == 1) {//若为奇数
int j = i;//当前奇数所处位置
while (j > k) {//j >= k+1 此处将该奇数移到最前面奇数之后
int tmp = array[j];
array[j] = array[j-1];
array[j-1] = tmp;
j--;
}
k++;
}
}
}
}
输入一个链表,输出该链表中倒数第k个结点。
双指针
public class Solution {
public ListNode FindKthToTail(ListNode head,int k) {
//双指针 快指针比慢指针多走k-1步,当快指针到达末尾时,慢指针在倒数k结点
if(k<=0)
return null;
if(head==null)
return null;
if(head.next==null)
return head;
ListNode slow=head;
ListNode fast=head;
int step=0;
while(fast.next!=null){
if(step<k-1){//当fast没走完k-1步时,只有fast走
step++;
fast=fast.next;
}else{//当fast先走完k-1步时,slow也开始走
slow=slow.next;
fast=fast.next;
}
/*
if(step>=k-1){
slow=slow.next;
}
step++;
fast=fast.next;
*/
}//当fast走到末尾,slow也走到了倒数第k个结点
if(step<k-1)//证明k>链表长度
return null;
return slow;
}
}
如有错误,欢迎指正
标签:power for 操作 fast slow void one 部分 ase
原文地址:https://www.cnblogs.com/lfz1211/p/12684509.html