标签:ilb cto 美的 利用 基本 平衡点 节点 限时 情况下
在介绍复杂系统之前,我们先来简单介绍一下还原论,还原论是对这个世界最自然的理解方式。它的核心思想是:“如果你理解了整体的各个部分,以及把这些部分‘整合’起来的机制,你就能够理解这个整体”。
一个最著名的例子就是牛顿的牛顿定律以及随之而来的“钟表宇宙”理论。

牛顿的定律则是动力学的基础,它们用力和质量作为基本概念解释了一切物体的运动,包括行星。
下面是著名的牛顿三大定律:

基于以上基本假设,牛顿力学描绘了一幅“钟表宇宙”的图景:设定好初始状态,然后就遵循着三条定律一直运行下去。
数学家拉普拉斯认识到其中蕴含了可以如钟表般精准预测的观念:他在1814年断言,根据牛顿定律,只要知道宇宙中所有粒子的当前位置和速度,原则上就有可能预测任何时刻的情况。
在20世纪40年代计算机被发明出来之后,这种“原则上”的可能似乎有可能变成现实了。
过了很久,1927年。突然来了个踢馆的。海森堡(Werner Heisenberg)提出了量子力学中的“测不准原理”,证明不可能在准确测量粒子位置的同时,又准确测量其动量(质量乘以速度)。
海森堡认为,对于其位置知道得越多,对于其动量就知道得越少,反过来也是一样。

再往后,混沌的发现给了精确预测的梦想最后一击。混沌系统说的是,对于其初始位置和动量的测量如果有极其微小的不精确,也会导致对其的长期预测产生巨大的误差。也就是常说的“对初始条件的敏感依赖性”。
这一点很不符合直觉,事实上,很长一段时间里,科学家们都认为这不可能。然而,混沌现象在很多系统中都被观测到了,心脏紊乱、湍流、电路、水滴,还有许多其他看似无关的现象。现在混沌系统的存在已成为科学中公认的事实。


第一个明确的混沌系统的例子可能是19世纪末由法国数学家庞加莱(Henri Poincaié)给出。庞加莱是现代动力系统理论的奠基者,可能也是贡献最大的人,大力推动了牛顿力学的发展。
庞加莱在试图解决一个比预测飓风简单得多的问题时发现了对初始条件的敏感依赖性。他试图解决的是所谓的三体问题(three-body problem):用牛顿定律预测通过引力相互作用的三个物体的长期运动。

正是在研究三体问题的几何结果的过程中,庞加莱发现了对初始条件的敏感依赖性。
换句话说,即便我们完全知道了运动定律,两组不同的初始条件(在这里是物体的初始位置、质量和速度),即使差别很小,有时候也会导致系统随后的运动极为不同。
此后,随着人们对复杂行为现象的不断发现,人们在尝试对简单个体的大规模组合中出现非线性复杂行为进行解释时,混沌、系统生物学、进化经济学和网络理论等新学科胜过了还原论。
尽管随着混沌理论的被提出,还原论遭到了现实事情的反面挑战,但是从定理上,尤其是从数学上证明还原论还没有令人信服的答案。直到三位著名天才科学家的出现。

希尔伯特、哥德尔和图灵
德国数学大师希尔伯特(David Hilbert)于1900年在巴黎的国际数学家大会上提出来三个问题:
复杂系统用来阐述模式的产生。现实生活中模式无处不在,例如:
上述这些现象,本质上就是自然界中模式涌现的过程。这些模式往往可以归结为组成系统的个体,通过简单相互作用达到某种复杂集体的现象。
复杂系统用动力学的思想阐述了这一过程的发生。
最典型的复杂系统的例子就是股市,大家都想预测股票价格,但实际上非常难做到,股票价格很难预测,这是因为股票价格本身即是大量交易者买卖之间涌现的一种宏观秩序,它与公司的业绩并没有直接关系(而是间接关系),公司业绩对股市的影响本质上是进入交易市场这个复杂系统的一个外部信息,外部信息影响交易者的心理但不决定他们的行为,最终股票价格是由交易者间的相互作用(博弈)决定的。
如果要研究股市,更多的应该去研究如何根据交易者所透露的蛛丝马迹推测其可能行为,但是根据复杂系统和混沌理论,即使你能够跟踪每一位交易者的所有行为和心理活动,股市仍然难以预测。
事实上,金融市场的不稳定性的根本就来自于复杂系统,这使得人们常常低谷风险,比如次贷危机。
人们依据的假设很多时候是把市场看作独立作用的部分,每个部分的风险是独立的。事实上市场的每一部分并没有独立,而是互相彼此作用,形成了一个混沌系统,正是它们的互相关联导致次贷危机。
讨论了复杂系统的基本概念之后,我们这章来讨论下,究竟是哪些因素,导致了复杂系统的产生。
不是单体的特性,而是单体是如何相互关联形成组织的。因为这些系统共同的特点是长程关联。关联往往导致1+1>2,或1+1<2,这称为非线性。比如为什么会有公司,其背后的原因当然有很多,从经济学、组织行为学角度都会有很多解释,从复杂系统角度来看就是,公司通过某种合作方法导致1+1大于2的效应使得公司可以产生。
整体系统的最终外显结果是受网络相互作用导致的,每个成员之间都受到邻居的影响,因此,相互作用是复杂系统的一个最重要的因素。例如,神经元就是通过相互作用构成神经网络来处理信号的。
由于相互作用的存在,使得物理系统无法轻松地由整体拆成部分,而是呈现出一种混沌状态。
混沌说的是由于系统内自由维度的增加,系统的动力学属性不再归于闭合轨道,而是开放或成为不可预测的轨迹,初始条件的轻微变化在未来的影响远未可知。
笔者提醒:
在复杂系统理论中,个体的属性与特殊性质不再是决定性因素,更重要的是个体之间如何动态地交互,彼此交换信息,形成一个复杂的整体。
复杂系统多用于描述一个系统的时间变化过程,比如市场价格的波动、神经网络随时间的活动等。研究这个时间变化过程,往往要考虑此刻的结果对下一刻系统输出的影响,例如股市就是一种典型的反馈系统。
反馈分为正反馈和负反馈两种:
在所有复杂系统中,都有正反馈和负反馈两种状态。反馈带有回路的概念,一个单元通过相互作用传递给另一个单元,反过来另一个单元又可以把信息传递回来。
一个典型的例子就是市场价格。市场价格永远围绕均衡波动,价格高,导致市场买的人变少,买的人少后又导致价格降低,这是典型的负反馈。负反馈吧系统维持在稳定位置,即dx=-x。
这是复杂系统的第三个重要特质,而且是组织形成的核心。当系统主导反馈的性质发生变化时,则经历一个相变。
相变在自然界和社会中无处不在,例如:
我们以磁铁为例来解释相变这个概念。磁铁这个东西,并非总是具有磁性,那么具有磁性和不具有磁性的磁铁有什么区别呢?
磁铁有两个相,
虽然它们都是由铁原子构成的,但铁原子只有在有序排序时才会产生磁性,而无序的铁原子使得每个磁针的磁性相互抵销了。
这里就建立了相的概念,而相变,就是通过外部变量使得整个系统从一个相到达另一个相的过程。
对于磁铁的相关过程来说,我们可以控制的外部变量就是温度。温度越高,磁原子的熵就越大,磁性就互相抵销;当温度为零时,系统自由能最小的状态是一致有序的态,即发生相变,称为磁铁。
类似的还有水到冰的相变,也是在某个温度上,无序和有序交替,这称为临界。
所谓临界,就是相变时候的状态,因为这个时刻是非常特别的。临界点上的系统属性特别复杂。
Relevant Link:
https://zhuanlan.zhihu.com/p/90083604 https://www.jianshu.com/p/3c0be8dddf37
单只行军蚁是已知的行为最简单的生物,如果将100只行军蚁放在一个平大部分蚂蚁种类的食物搜索大致是这样进行的:面上,它们会不断往外绕圈直到体力耗尽死去。
然而,如果将上百万只放到一起,群体就会组成一个整体,形成具有所谓“集体智能(collective intelligence)”的“超生物(superorganism)”。
大部分蚂蚁种类的食物搜索大致是这样进行的:
蚁群中的工蚁分为四个工种:
执行各种任务的工蚁数量能随着环境变化。戈登发现,如果蚁穴被稍微搅乱,维护蚁穴的工蚁数量会增加。如果附近的食物源很多,质量很好,搜寻食物的工蚁数量就会增加。单只蚂蚁可以根据蚁穴环境的变化作出适应性响应,决定采取哪种工作,无需另外的蚂蚁来指挥,每只蚂蚁也仅与其他少数蚂蚁交互。
答案可能是蚂蚁根据它们周围的环境以及它所遇到的执行各种任务的蚂蚁比例来决定自己干什么。
同大脑一样,不同动物的免疫系统复杂程度也各不相同,但总体上的原则是一样的。免疫系统由许多不同的细胞组成,分布在身体各处(血液、骨髓、淋巴结等)。这些细胞在没有中央控制的情况下一起高效地工作。
免疫系统中的主角是白细胞,也称为淋巴细胞。白细胞能通过其细胞体上的受体识别与某种可能入侵者(比如细菌)相对应的分子。
有一类细胞被称为B细胞(B是指它们产生自骨髓,Bone marrow),它具有一种奇特的性质:B细胞与某种入侵者匹配得越好,它产生的后代细胞就越多。这样就形成了达尔文自然选择机制,B细胞变得与入侵者越来越匹配,从而产生出能极为高效地搜寻和摧毁微生物罪犯的抗体。
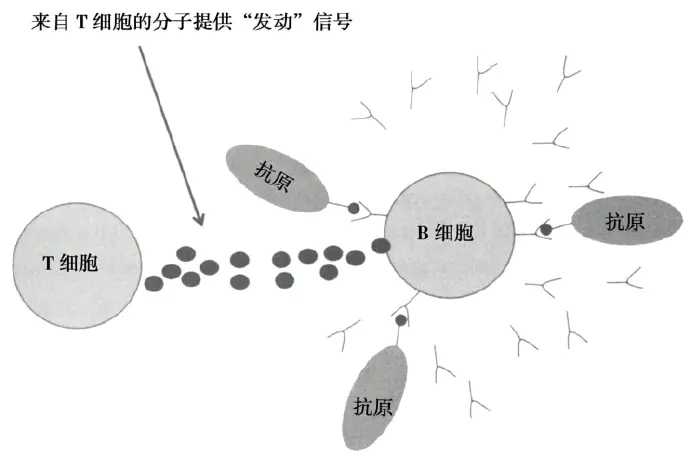
首要前提我们要知道一点:身体中所有细胞表面都有称为受体的分子。顾名思义,这些分子是细胞接收信息的途径。信息表现为能与受体分子结合的外界分子。
一类淋巴细胞表面覆盖了一类特定的受体蛋白形态,可以与特定的某一类分子形状匹配。如果恰好遇到了形状相匹配的病原体分子(称为“抗原”),淋巴细胞的受体就会与其相结合,淋巴细胞就“识别”出了抗原,这是消灭病原体的第一步,这一步产生了激活的B细胞。
激活的B细胞被输送到淋巴结,在那里迅速分裂,产生出大量后代,复制时由于变异,许多后代的受体形状都改变了。然后这些后代会与淋巴结俘获的抗原进行测试。不能结合的细胞很快就会死去。
接下来,带着这些信息的B细胞就会向血液中释放抗体分子。这些抗体与抗原结合,使它们失效,并对它们进行标记,好让T细胞细胞摧毁它们。
从某种意义上讲,人类的大脑与蚁群十分相像,两者都是由相对简单的个体组成,个体之间只进行有限的通讯,整体上却表现出极为复杂的系统(“全局”)行为。
在大脑中,简单个体是神经元。除了神经元,大脑中还有许多不同的细胞,但绝大多数脑科学家都认为是神经元的活动以及神经元群的连接模式决定了感知、思维、情感、意识等重要的宏观大脑活动。
生物归根结底都是自私的——它们要想在进化中获得成功,就必须能活足够长的时间,保持足够的健康,还要能吸引异性,以繁衍后代。大部分生物为了达到这些目的会毫不犹豫地与其他生物进行斗争,采用各种伎俩,杀死或杀伤其他生物。通常的看法认为进化选择会使得自私或自卫本能得以传递给下一代并在种群中扩散。然而与这种看法相反,在生物王国和社会的各个层面上都有许多明显不符合自私原则的例子。
从底层看,在进化历程的一定阶段时刻,单细胞生物会互相合作以形成更复杂的多细胞生物。
这不仅仅是个科学问题,也是政治问题:例如,是否有可能创造条件让国家之间产生并维持合作,一起应对核扩散、艾滋病、全球变暖等国际问题?
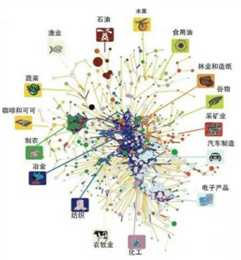
世界经济产业森林
上图描述的是一个一个叫产业森林的图。产业森林描述了一个由种类繁多的农业和工业产品组成的关系网。每一个产业即网络里面的一个节点。
对于产业森林图来说,最重要的概念有2个:
事实上,不同产业之间不是孤立的,这里所说的产业之间的相似度,其实就是构成它们的技术或生产资料要素的相似性。我们可以规定超过一定相似度阈值的两个产业就可以被联系起来,这样,即可得到一个结构复杂的网状结构图。例如“生产苹果”和“生产梨子”的相似度就很高,如果一个地方适合栽种梨树,那么它往往也适合栽种苹果。
森林中心是高级工业品,森林边缘是农产品和原材料等。森林中心树木密集,树木间盘根错节(产业间连接紧密),而森林边缘树木稀疏,树木间连接也相对较少,甚至在有些森林的边缘,有些树木基本就是孤立的,比如奶牛生产。接下来的问题是,这样一个网络结构究竟有什么作用呢?传统理论认为这样一个结构图没有什么用,因为条条大路通罗马,只要经济在积累,总有机会到达果实丰硕的森林中心,但事实真的是这样吗?
但是复杂网络理论则告诉我们一个完全不同的答案。
首先,一个企业往往用它所占据的较为优势的产业来表示。一个企业的发展,被称作从森林的某些位置向其他位置跳跃的过程。
可以把企业比喻成产业森林里跳跃的猴子,它可以从一棵树跳向另一棵树(产业升级)。当然,猴子的目标肯定都是朝着果实丰硕的中心去的。
传统的研究认为,如果一个猴子长期无法到达中心,一般认为是猴子的问题,一个预先的假设是猴子只要跳的足够好,总能从一棵树跳到另一棵树,并最终到达森林的中心。但现实情况是,我们会看到有很多优秀的猴子(明星创业者和明星创业项目,但是没有最终发展上式)没有能成功跳到森林中心,这是为什么呢?
我们用森林的结构来阐述为什么有的猴子能够到达森林的中心而其他猴子不行,因为森林的结构是很重要的制约因素。
网络的性质至关重要,
前面也提到过,森林的边缘树木如同独立的孤岛,而中心的树木密集。而猴子的跳跃能力是有限的,猴子从森林外侧向中心跳跃不是一件容易的事情。
当猴子所在树的周围树木过少且树木间距过大时,猴子就无法调到下一课树上。而森林中心的猴子可以很轻松地在树木之间跃迁并摘取丰美的果实,而边缘的猴子则没什么选择。这就是所谓的“winner take all effection”。
另一个发人深省的现象是猴子能否进入森林的中心和它所在的初始位置以及它在每一次跃迁中选择的跳跃方向十分相关。
以上面的产业森林图为例,我们看到劳动密集型工业(汽车制造)和电子产品工业是一条由森林边缘通往中心的捷径,品种繁多,相距很近。
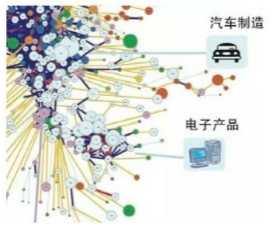
相比之下,热带作物(咖啡和可可)一直处在森林的边缘,与森林中心差距较远(仅橡胶与工业品联系较密切),各种热带作物间也距离较远。
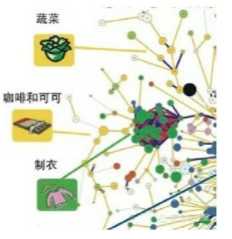
曾经一段时间,主宰统计世界的是一个叫“高斯分布”的函数,它的英文”normal“含有正态、标准之意,说的是决定事物整体性质的是它的平均,例如我们可以用1米7代表整个中国人的身高。
我们经常用平均数表达事物的总体状况,对于做统计的人,平均数几乎成为信仰,这种信仰背后的基本假设是:只有在我们统计的事物呈现高斯分布时,平均数才能够代表事物的属性。
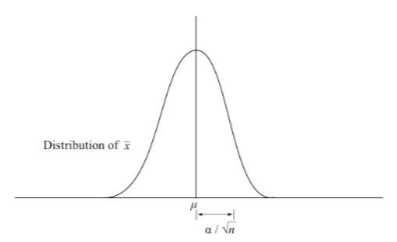
高斯定律让我们看到了加法的为例。对于一个随机事件,比如掷骰子,虽然每一次取得的结果从1到6完全无法预测,但是如果掷一万次,把每次掷的点数加起来就能得到一个可以被越来越精确预测的数。
这个结果可以被一条高斯曲线(本质上就是似然函数)描述,它具有两个特征量:
随着加数的增多,标准差在平均数面前越来越微不足道,知道可以忽略不计,或者说通过无穷加和,一个随机事件无限接近成为确定事件。这条法则就叫做大数定理(Law of Large Number)。
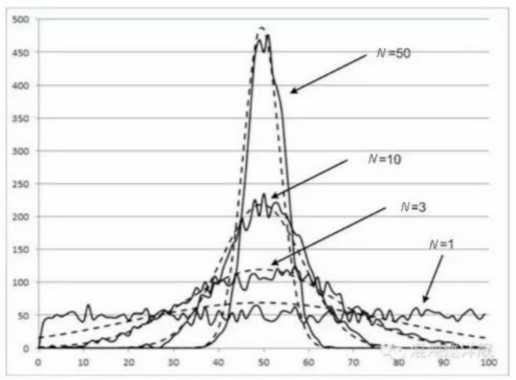
但是!要特别注意的是!正态分布有两个非常关键的成立假设!
大数定理的威力,在于它使得一个确定性的世界可以在庞大的不确定性之上产生。
正态分布和大数定理是所有确定性的根源,因为我们的可见世界就是无数不确定的微观因素不断加和的结果。
高斯定律和大数定理保驾着庄严的理论物理世界,在这里,气体分子之间符合理想模型、光滑水平面和无相互作用、好好学习就能天天向上。然而,现实世界中,黑天鹅摧毁了童话。
基于高斯分布的各类数学工具主宰者庞大的金融帝国上百年,却成为21世纪初金融危机的罪魁祸首。这背后的缘由,正式复杂性主导的黑天鹅效应。
在黑天鹅出现前,天鹅湖里的天鹅都是白色的,你可以想象那种天蓝色的湖面上飞起千万只白天鹅的感觉,远远看去如同乞力马扎罗的雪。
于是我们把白色当成天鹅的标志,以趋于100%的概率预测天鹅皆白。直到有一天湖面上飞过一只纯黑的天鹅....

从而我们明白,在生物界,特例才是本质,而不是平均。特例总会以比你预想的还要大的概率出现,而把之前的理论打得粉碎。
黑天鹅的本质是个体对总体、细节对全局产生决定性的影响。
用高斯的正态的观点来看,黑天鹅出现的概率本来可以忽略,因为我们之前已经统计了巨大的白天鹅样本,但黑天鹅还是出现了,是我们的运气特别不好吗?不是的!是幂律分布在作怪!
在生物世界中,起主导作用的是幂律分布(Power Law)。
幂律分布的数学表达简洁无比,不同的幂律分布只体现在幂指数的不同之上。它与高斯定理的本质不同在于,高斯正态分布下那些概率小到可忽略的事件,在幂率分布下却没有那么罕见。
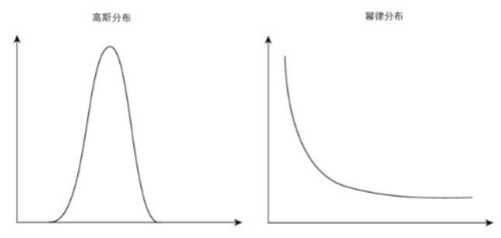
在幂率分布的观点下,严重偏离平均值的黑天鹅的出现是可以理解的,罕见的黑天鹅不仅来到,而且决定着全局。同样的例子还有经济学中的帕累托效应,即20%的富人掌握80%的财富。

社会财富的二八定律
另一方面,局部的特征与全局特征具有自相似性,幂率正是它的数学表达,

Mandelbrot Set分形结构

海岸线分形

树叶中的分形结构
为什么黑天鹅影响如此之大?现代物理中的相变理论给出了有力的答案。下面用一个具体的例子说明,即雪崩。
雪崩是山顶大面积的血蹄坍塌,本来要倒推一座雪山几乎是不可能的事情,因此雪崩符合经典的黑天鹅事件的定义,按常理几乎不会发生,一旦发生即致命。但是为什么在现实中我们会经常听到雪崩的事故呢?
雪崩的诱因非常小,可能就是一粒小石子打到雪山上,或者一个人在喊话,这些微小因素在绝大多数情况下都对雪坡毫无影响,但是在一种特殊的情况下,即雪体的临界状态,就会发生雪崩。
临界状态是一种脆弱的平衡状态,维持雪体凝聚在一起的力量和使雪体瓦解的力量几乎相等,但是只要天秤一边稍微受到一点扰动便万劫不复。
在庞大的雪坡上投一粒微小的石子,石头的作用力不是被局部的雪体吸收,而是扩散到整个雪体,如同压死骆驼的最后一根稻草,使平衡整体倒戈。
黑天鹅本身并不能直接导致相变,而是临界状态的存在使得黑天鹅成为决定性力量。
雪崩理论的核心是临界状态下细节的作用被无限放大(正反馈)。一个本来只限于局部的小因素在临界状态下扩散到全局。雪崩理论遍布各个领域,例如地震、股市崩盘、金融危机。
生命洪流的本质是一种特殊的相变,因此所有生物的历史以及我们人类的一生,都无时无刻不在发生临界状态,那个小小的雪崩的状态,那个不可预见的细节决定了全局的状态。既然明天还活着,黑天鹅就随时会起飞。这对我们日常应对风险的策略,具有深刻的启示。
我们的生命过程就像一个盲人摸象的过程,无论站在哪个时间点,你的信息量都非常有限,根据非常局部的信息做出最优选择的机会几乎为零。庞大的世界,复杂的历史,我们都捆绑在自己的路径上,在黑暗里瞎摸。
面对这种情况,最好的办法就是不停试错,任何过度思考和过度计划都是多余的。
我们应该通过快速摸索,增加你对周边信息的把握。每一次错误,你都可以根据它矫正你对世界的判断,这样,几轮之后,你得到正确选择的概率将会大大增加。
一个利用试错进步的典型例子就是市场经济。
市场经济把经济活动的自主权还给个体,虽然每个个体都不是很聪明,但是它们都有一个特点,知错就改,唯利是图。它们所主宰的经济,试错和纠错能力都是超强的。其结果是,短时间内资源分配就接近了最优化,虽然还有点波动,但仍超过世界上最厉害的经济学家的预测能力。这也是凯恩斯自由市场理论的核心思想。
市场经济是反脆弱的,每一次意外的小概率事件,即黑天鹅事件发生时,它都可以调整过来,并且变得更加成熟,自由市场调节平衡的能力十分惊人。
自然界应对无常环境进行的一种典型运动方式是先确定一个的的区域,然后做小范围改变(试错),如果得到的反馈信息是不利的,就快速做出一系列大幅度的调整,直至达到一个比较有利的位置,这样的变动周而复始。
这是一种应对无常最佳的适应方法。如果环境丰饶,则快速跟进,不失良机。反之,又不至于过分执着于不够好的机会而被困死。
一个典型的例子是鲨鱼觅食。鲨鱼在鱼类丰富的环境进行小步伐的随机游走,只要不停地游动就可以吃到最多的鱼。但当鱼类相对不足的时候,鲨鱼就会进行大步伐的跃迁,这种跃迁也是随机的,却具备一次改变较大的特点。
小步伐的随机游走比较容易穷尽开采一个地方的资源,但不容易到达较远的地点,而大步伐的跃迁却有利于开发新的领地,寻找新的食物来源。
整个宇宙都可以理解为在随机运动下导致对称破缺(有序产生)的过程。
笔者思考:
对于复杂系统,我们只需要管理某些对系统产生核心影响的事件,而对其他事件放任,让自然来管理。
抓大放小,就是在能量有限的情况下,专注于做重要的事情。若是把精力过多地放在微小因素上,就会无暇顾及核心因素。而微小因素往往会在恰当的时候自发解决。老子所说的无为而治,就是指大自然早已给我们设计好了节能优化模型,把一些事情交给自然,剩下的事情才可以尽力到底。
前面的两种策略都属于被动避险策略,现在我们反其道而行之,反向利用“无常”和“分布函数”尝试进行获利。
所谓杠铃策略,是一个形象化的指代,杠铃两头重中间轻,其实它就是无常的化身,幂律函数的缩影。
幂律函数有两个特点:
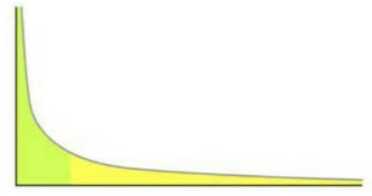
杠铃策略,就是同时把握大头和长尾,利用分布函数获利。
下面利用复杂系统的非线性动力学分别介绍”弱杠铃策略“,以及仅利用分布函数形状的策略的”强杠铃策略(杠杆原理)“。
最简单的应用莫过于高风险和低风险事件的组合。比如,
杠铃策略的另一个典型应用是人的知识结构,最有效的知识结构亦呈现幂律分布,专一的技术是头,光波的知识是尾。专一技术是人立足江湖的必杀技,但是在很多特殊的关键时刻,广博的知识又起决定作用。在巨大的未知性面前,仅有专一的技术往往是脆弱的,就像溺水的人工智能专家,决定他命运的不是计算机知识,而是是否会游泳。
弱杠铃策略强调互补,而风险对冲则强调相反相成。简而言之,就是一种事物的风险,恰恰构成另一种事物的机遇。
杠铃一端的损失就是另一端的收益,当一端向下时,另一端恰好向上。聪明人利用这个杠杆,把生活中向下的波动转成向上波动的契机。
对冲的基础其实是事物的非线性,如果你同时买进分布两端的事物,而这两个事物又存在反向关联(当A下降时,B有上升趋势,或反之)。最关键的是,这种关联是非线性的(A的下降不等于B的上升,下降总是小于上升),一端小的下降总会引起另一端较大的提升。
这种非线性的对冲,保证了在任何情况下,你的收益都为正。
懂得在生活中使用对冲法则的人从不会焦虑或者为任何事请沮丧,
杠铃策略之一就是实用主义和理想主义的结合。最优秀的理想主义者,往往要奉行最强大的实用主义原则,理想和实用就是杠铃的两端。
懂得杠铃主义的人会把一些事情用最大的实用主义解决,然后就可以无忧无虑地搞理想。
小概率的黑天鹅事件,是网络安全最常见的现象。无论我们积累了多少领域经验,或者是动用了多么庞大的训练样本集,小概率的误报事件总是会不定期地出现。
Relevant Link:
https://www.jianshu.com/p/ee54998e4d60
非线性动力学,是用物理学的思维理解复杂系统的一座丰碑,也是非常有前途的工具学科,它为大数据时代提供了潜在的分析引擎。
之所以说非线性,是因为物理之外的系统大多数不能用线性系统表述。
动力学的核心使命是预测系统的变化,非线性动力学的核心使命也是如此。一个经典的非线性动力学系统具有如下标准的表述形式:
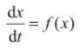 ,x是一个向量(vector),它所具有的分量个数即系统的维度
,x是一个向量(vector),它所具有的分量个数即系统的维度
预测一个系统的未来,你需要知道它在微小时间尺度里的性质,并列出动力学方程。
维度是动力学系统的最基本属性,它决定了系统的复杂性,以及其可能具有的基本性质。我们本章将从低维到高维,逐层递进讲述复杂性是如何随着维度的升高而产生的。
最简单的系统是一维系统,预测一个一维的非线性系统,往往只需抓住一个关键性信息,定点。
18世纪末,在工业革命前夜的英国,一个叫马尔萨斯的思想家提出了这样一个困扰人类几个世纪的问题:人类的人口呈现指数增长,而食物的总量至多成代数增加,所以当人口的增加超过食物时,人类将不可避免地陷入饥荒、疾病和战争。而普遍性的贫穷,是人类文明的宿命。
这个理论解释了为什么许多古代文明陷入发展停滞的泥沼,例如埃及。
马尔萨斯的理论,其实诠释的是一个叫作Fix Point(定点)的动力学概念,即在一个复杂系统里,事物的增长往往不是线性的,而是存在一定的稳恒状态,系统的变化会逐步减速并自发地把自己维持在这个状态上。这样的现象在生活中不胜枚举,例如:
马尔萨斯的人口论符合一个叫作logistic model的经典一维动力学模型,它也因为它美妙绝伦的S曲线而闻名。
这个模型说的是,在没有环境压力的时候(人人吃饱饭),人口的增长率是恒定的,所以人口的增加会呈现出指数增长。但是一旦人口接近环境的阈值,就会有人开始饿死,而且饿死的比例会随着人口的增加而增大(负反馈)。这样,当饿死的人数量等于出生的人的数量时,两个此消彼长的要素就在某个点上平衡了,即所谓的定点。
反映在数学谁给你,就是这样一个微分方程:
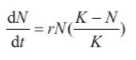
所谓的定点,就是使该微分方程(人口变化率)为零的点,当人口数恰好处在这个点上时,就会不增不减。
这个定点具有一个更深刻的性质,无论人口一开始是多少,只要K给定,系统就会趋于一个相同的值。这个值由环境本身的容量所决定。
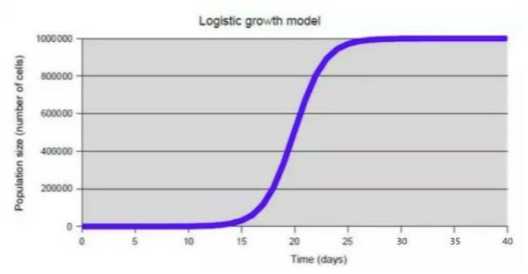
除了人口增长曲线之外,S型曲线(sigmoid function)的身影在自然界比比皆是,反映了自然生产的一般规律。
动力学里最重要的额概念之一是定点,但是定点本身却只有很少的信息,更关键的性质来自于对定点周围区域的分析,或者说定点的稳定性。
我们用一个被称为稳定性的概念来描述这一特性。稳定性描述的是系统处在定点周边的状态,它是比较容易进入定点还是比较容易离开。
从物理的角度很容易理解一个定点是稳定的还是不稳定的,只需要稍微离开定点,看一下系统的运动情况,看看系统在定点的相邻区域里的运动趋势怎么随位置变化的。翻译成动力学语言就是在定点周围进行泰勒展开,并取一阶线性近似(在一维情况下就是我们熟悉的斜率,在高维情况就是雅可比矩阵的特征值)。如果在定点周围的运动趋势指向定点(线性的斜率为负,或者雅可比矩阵特征值为负),则定点在局域内稳定,反之则不稳定,如下图所示:
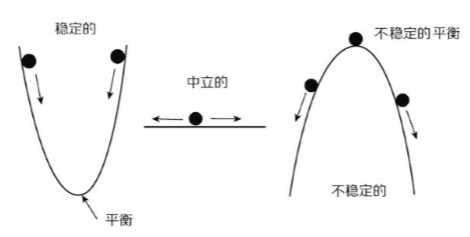
定点的稳定性,取决于泰勒展开的不为零的第一项的正负
稳定性,还有另一个同名词叫吸引力。一个稳定性定点,就像一个区域里的黑洞,它能把进入其辖区内的所有人都吸收到它的点上。它所管辖的区域,被称为Basin of Attraction。它是强韧性的代表,不论你怎么干扰它,迫害它,结局终将归于它。
找到Basin of Attraction是利用定点预测系统的必备条件,给定一个系统,如果它的初始位置处在Basin of Attraction,那么它将永远停留在该点上。
不稳定性就是脆弱性的代表,任何环境的风吹草动都能结束它表面的美丽和平静。而最强的定点具有全局稳定性,即无论任何初始条件,系统都将趋于这样的定点,这样的系统就是高度可预测系统。
大部分时候,很多系统是稳定点和不稳定点成对出现。比如前面说到的人口模型,人口为0就是一个不稳定平衡点。当人口为0的时候,它可以永远为零,但只要系统的人口增长了哪怕1,它就是不可阻止地趋于定点K,掌控系统除0之外所有区域的稳定点。这就是黑天鹅幂率效应。
在开始讨论之前,读者朋友们可以先思考几个问题:
要解决这些非常基本的问题,我们需要一个二维的动力学系统。二维可以描述一个比一维丰富得多的现象,正如同物理学从描述两个物体的相互作用开始描述了世界。
一维的系统往往归于单调的定点,而二维系统的主角缺失振动,也是人类几千年来描述自然最有利的工具。
从自然到人类,世界可以看作异步不同频率振动组成的交响曲:
几乎有运动的地方,就有振动。
为什么振动的形式如此广泛地存在?其本质是因为定点的广泛存在。振动就是围绕一个确定状态的上下波动。就好像希腊神话里的西西弗斯,把石头推上山,在到达山顶时又立刻滚落下去,然后他又推上山,他想让石头停在山顶不动,可却做不到。
为什么振动如此普遍,非线性动力学之父庞加莱给出一个定理,条件如下:
庞加莱得出结论:该区域内的动力学流将收敛于一条闭合轨道。
简单来说,
相平面的闭合轨道=周期性运动=振动
这个定理告诉我们,有限二维系统里的运动形式只有两种:
由于自然界中负反馈普遍存在,因此系统不会无限取值或发散,因此系统是有限的。这条定律解释了振动普遍存在的根本原因,它是二维运动的范式。
庞加莱定理告诉我们,二维动力学流,不是流向定点,就会形成闭合轨道。这条定理确立了非随机的二维系统的绝对可预测性,二维系统没有混沌。
当我们发现振动,就可以去系统里寻找有没有两个关键性的动力学变量,并且观察这个系统是否有稳定的平衡态。如果没有平衡态,则往往预示着该系统存在着一个无定点的闭合区域。
经典物理的振动核心在于能量守恒,无论是弹簧的上下振动、单摆的往复振动、还是电子波的正弦振动。对这类系统的传统解法是对微分方程进行积分,以得到运动的轨迹。但是利用一些动力学的基本知识我们也可以完全不用积分就能了解它的运动性质,如下图所示:

下面以单摆为例。首先,将微分方程写成标准的二维动力学系统形式,即体系内有两个动力学变量:角度和速度。
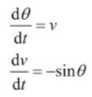
然后,寻找定点(动力学流为0),显然是 θ=0,v=0。
接下来,看看该定点是否可以达到,显然,只要系统能量不为0,就不可能达到该状态。
最后,系统是否在相平面内封闭?答案是肯定的,因为恢复力-sin(θ)起负反馈作用,根据能量守恒定律,θ和v均在有限区间取值。
因此,系统在相平面内,收敛到一个圆周封闭运动中,如下图所示,
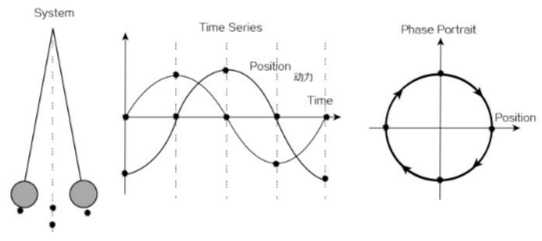
当一个系统有能量流入流出时,我们称之为开放系统,对于一个二维的开放系统,庞加莱定理依然成立,系统若不归于平衡,则步入永恒的循环。
对这类系统来说,显然有比两个多得多的变量,但是如果把关注重点集中在它们进行周期性运动的时间范围,往往可以抽象并抓住两个关键性变量,并用二维动力学系统的知识来解决。
一个最典型的例子依然是关于物种数量的例子,前面说过,一维的人口模型里人口将达到定值,而事实上,自然界中的物种数量却是震荡变化的,这是为什么呢?
要解决这个问题,就需要对自然界物种之间的关系进行抽象简化,讨论两两物种之间共存的情况(二维)。
试问下面的问题,在一片草原上生活着狮子和羚羊,狮子吃羚羊,羚羊吃草(假设草是无限的),假设一开始物种数量是均等的,那么后来两个物种的数量变化会是怎样的呢?
显然,两个物种间有相互作用,
这个系统可以用一个Lotka-Volterra方程的经典二维动力学系统表述:
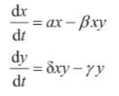
接下来的问题是,如何预测两个物种的数量变化?
首先进入相平面,我们看到系统的流形(每一点的微分(dx,dy)构成一个向量,画出箭头犹如流体力学的流速线)。
然后我们分析定点,二维系统里含有两个微分方程,如果一个微分方程为0,例如dx=0,我们将得到一个代数关系x=k xy,在相平面里这对应一条线,即Nullcline。在这条线上,第一个变量处于平衡态。同样,我们可以找到变量y的Nullcline,对应相平面的另一条线。这两条线如果有交点,即二维系统的定点,或者说系统的平衡态。
这个问题可以很容易找到四条Nullcline和两个定点:
对第一个定点(0,0)来说,代表两个物种都灭绝了,这种情况是羊死光了才会出现。因为假设狮子死光了,羊就会无限增长(远离定点)。在相平面上,就表现为动力学流沿着y轴(对应羊死光的情况)收敛为0,而沿着x轴(对应着狮子死光的情况)发散,如下图所示:
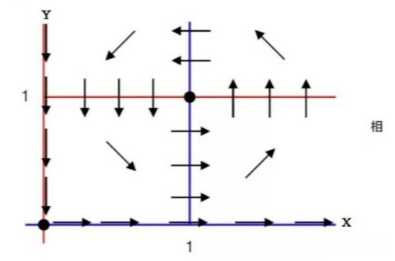
这一现象的隐含含义是(0,0)点在x方向上是不稳定性定点,而在y方向上是稳定性定点。
这种在一定方向上收敛,而在另一些方向上发散的定点,被称为Saddle Point(鞍点)
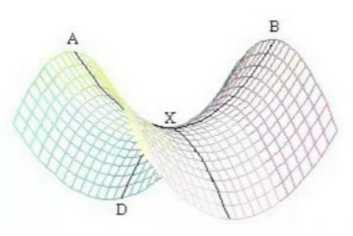
再来看看另一个定点,即第一象限内的定点(a,b),它描述两个物种数量互相制约的平衡状态,看似是一个合理的结局,即狮子和羊的数量达到平衡,这不就是所谓的生态平衡吗?
如果这样想,那么就是停留在初中生物课层面了。在这个定点周围找几个点,通过画出(dx,dy)的箭头即可知道,它们都不是朝向这一点,而是围着这点转圈。
利用庞加莱定理可知,系统将永远不能陷入这个点,而是围绕这个点形成闭合轨道,即震荡。系统的两个物种的初始数量只要不是有一个灭绝或恰好一开始就匹配平衡,都将形成一个振动变化关系。
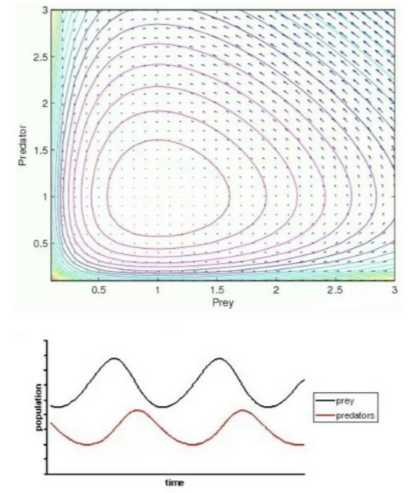
生态学中真正的稳定性,其本质是动力学系统里振荡。
Lotka-Volterra系统在经济学中也有重要应用。凯恩斯学派用以解释劳动雇佣资本率和资本的周期性振荡。这一理论把资本对应为狮子,而劳动雇佣率是猎物,两者总是不能自发地处于定点(100%雇佣率),而是长期处在周期性的振荡状态。
整个凯恩斯理论都可以放入一个简化的二维动力学系统。生产和需求作为一对互相追捕却永远捕不到对方的对手,将陷入不停歇的振动状态,即经济周期。它导致经济运行不可避免的在一定时间内走向低谷。
二维系统可稳定存在的运动状态有两个:
这两种状态可以转化,有的是从一个定点到另一个定点的转化,也有的是定点和振动之间的转化,这就涉及一个非线性动力学永恒的主题,Bifurcation(分叉)。
我们用分叉研究一个动力学系统的演变。动力学系统由状态变量(系统可以自由变化的量)和控制变量(参数)组成。在二维的世界里,参数给定后,即可得出动力学流型,从而一切皆可精确预测。
真实的世界从来没有一成不变的参数,真正不变的只有变化,甚至有的时候参数和变量甚至难以区分。
因此,非线性动力学给出了对世界的最精密的描述,不是确定参数下的流型,而是在参数空间里对应的不同相平面的流型。简单地讲,动力学不仅感兴趣我们所在的世界,而是所有可能的世界(一参一世界)。参数的空间好比一个小径分叉的大花园,每一点上都有一扇窗户,打开后就可以看到那个世界的可能性。在这个花园里,我们可以看到一种可能性是如何演化成另一种可能性的。
这么说有些抽象,我们以二维世界为例,如下图:
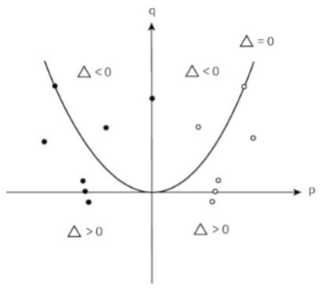
可以看到十字线和一个抛物线。这是最简单的线性二维动力学系统,完全可以通过求解系数矩阵的特征值解决。
首先看这个系统的定点(0,0),系统是被这个定点牢牢抓住,还是围绕它振动,还是远离它而去,则取决于系统的参数。
这个平面的横轴和纵轴代表了这一矩阵特征值的实部和虚部。当系统的参数变化时,表现为系数矩阵的特征值在这一平面上的运动。
那么什么是Bifurcation呢?它本质上就是参数空间里系统动力学流的性质发生质变的点。例如上图中的抛物线顶点。当系统的参数变化越过抛物线时,系统就从稳定吸引变成了发散原理定点,这个过程就是Bifurcation。
Bifurcation标志着系统的动力学性质发生彻底的变化,好比两个人在路上走着走着,突然到了岔路口,从此南辕北辙。
在动力学家的眼力,只有那个Bifurcation Point具有关键意义,可以起到区分不同系统的作用,其他小的变化都忽略了。
Bifurcation正是物理里相变的化身,在动力学的世界观里,定量的改变等于没改变,而只有Bifurcation才是真正的变化。物理、化学、生物一切最有趣的现象,都在Bifurcation Point上,因为它的敏感,成就了它的无限可能。
当系统的维数达到三维时,主宰动力学模型的就不再是那些稳定可测的点或圆环,而是初值敏感,极难预测的混沌。
混沌其实不是说完全随机不可预测的系统,系统依然具有确定性的方程,只是其复杂性使得它看上去像是随机的、毫无秩序而已。
对三维系统的稳定状态,就是三维空间里复杂的曲面,我们称之为吸引子,是三维空间里吸引系统进入的一个物体。
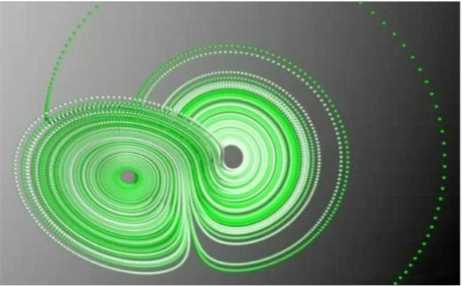
下图为洛伦兹吸引子的形状:
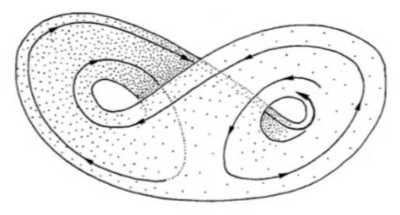
为什么说三维非线性系统可产生混沌?因为物体被一整个曲面吸引,不知道往哪里去了。即使它被禁闭在这个曲面上,也可以具备无数的轨道(面上的曲线),轨道变得复杂不可预测,因而表现出混沌的样子。
洛伦兹以它优美的洛伦兹方程证明了混沌是如何从一个三维的确定性系统里产生出来的。
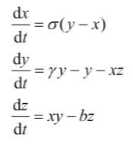
下图为洛伦兹吸引子,由洛伦兹方程确定的三维系统具有两个吸引中心(定点),系统围绕两个定点旋转,形成极为复杂不可捉摸的轨道,形如扇扇翅膀的蝴蝶。
对这一系统最简单的理解是,洛伦兹系统依然描述闭合轨道,这和之前描述的二维系统的振动是相同的。
但是在三维系统里,我们有两个定点,以及随之确定的吸引子曲面。系统时而围绕着其中一个定点旋转,时而围绕着另一个定点旋转,但是什么时候改变围绕旋转的对象却是不可知的,或者说是概率性的。
混沌准确的定义是相邻轨道的稳定性,或者说初值敏感性。
混沌实则是复杂秩序的产生者,它所产生的秩序,叫作分形结构(fractal)。分形结构的本质是自相似性,或者说标度不变性。
Relevant Link:
《机器学习 vs 复杂系统》
标签:ilb cto 美的 利用 基本 平衡点 节点 限时 情况下
原文地址:https://www.cnblogs.com/LittleHann/p/12674842.html