SINGLE-IMAGE DERAINING USING AN ADAPTIVE NONLOCAL MEANS FILTER论文分析（以公式分析为主导）

标签：bsp   条纹   运算   中心   back   恢复   缩放   计算   经验   

文章摘要（基于自适应非局部均值滤波器的单图像去雨）：

　　提出了一种适用于单幅图像的自适应雨条纹去除算法。我们观察到一个典型的雨带有一个垂直方向的椭圆形拉长。因此，我们首先通过分析椭圆核在每个像素位置的旋转角度和长宽比来检测雨痕区域。然后通过自适应选择非局部邻域像素及其权值，对检测到的雨带区域进行非局部均值滤波。实验结果表明，与传统算法相比，该算法能更有效地去除雨滴条纹，恢复图像质量更高。

文章核心方法：

　　该算法采用非局部均值滤波去除雨滴条纹。然而，假设像素被零均值高斯白噪声污染，非局部均值滤波器被用来对图像进行去噪。雨景图像的特点与噪声图像有很大的不同。具体地说，与独立的噪声分量不同，雨条纹由具有底层结构的连接像素组成。此外，与零平均噪声不同，雨点像素的值通常大于雨点像素的值。因此，如果非局部均值滤波器直接应用于降额，它可能会导致雨痕周围的模糊伪影，并使恢复图像比输入图像更亮。为了克服这些缺点，我们首先检测雨滴条纹（区域），然后将非局部均值滤波器自适应地应用于雨滴像素

具体方法：

非局部均值滤波器：

[8]中的非局部均值滤波器通过用整个图像中非局部相邻像素的加权平均值替换噪声像素来降低像素噪声。换句话说，像素p的颜色I（p）被处理成滤波后的I~（p），即它的非局部邻域q的颜色I（q）的加权平均值

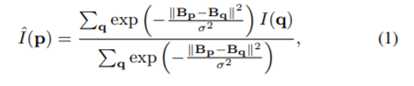
 以P为中心点的其邻域所有加权平均值则是I~(p)

其中，Bp和Bq是列向量，分别表示以p和q为中心的块内的像素颜色，σ是高斯参数。注意，当块Bq更类似于块Bp时，在加权平均中I（q）被赋予更大的权重（即Bq和Bp的平方距离越小，权值越大）。在这项工作中，每个像素q的颜色I（q）是RGB颜色空间中的三维向量。(一般是通过灰度值来处理的)

　　雨纹检测利用形状和方向特征检测雨纹区域：我们假设每个雨带都有一个椭圆形状，并使用[9]中的核回归方法提取图像中的椭圆分量。让Wp表示以像素p为中心的窗口。我们使用协方差矩阵Cp分析Wp的结构，该矩阵由

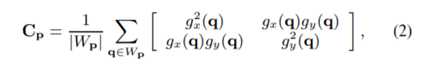
　　其中gx（q）和gy（q）分别表示水平方向和垂直方向上的像素q处的梯度值（不明白为什么这里用梯度值来表示），| Wp |是Wp中的像素数（除以| Wp |是做均值处理）。我们只使用从RGB颜色向量中提取的亮度值来获得梯度。

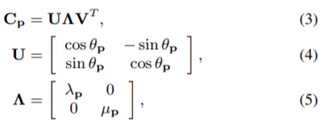
在Wp中，椭圆的形状和方向可以通过将SVD应用于协方差矩阵Cp来确定，即如式子3、4、5所示。

其中U和∧分别是旋转矩阵和缩放矩阵。此外，θp是椭圆核的旋转角（知道转角后便于旋转），两个特征值λp和μp表示主轴和主轴方向上的核尺度（便于缩放）

SVD的主要作用是提取矩阵Cp中的特征，本文中可以通过该方法获取θp、λp和μp的值。SVD的详解见补充。

然而，（2）∼（5）中的核回归方法可能会受到窗口内其他图像结构（例如对象边缘）的不利影响。为了减轻其他结构的影响，更可靠地检测雨带，我们在（2）中通过自适应地对每个像素处的梯度加权来修改协方差矩阵。我们利用雨条纹的三个特性：首先，雨像素往往比无雨像素更亮。其次，雨带具有空间紧凑的形状。第三，雨带中的像素有相似的颜色。

第一个属性与像素的亮度级别相关。如[3]所述，雨带区域中的像素通常比无雨区域中的像素亮。因此，我们使用像素q的亮度Y（q）和窗口Wp中的平均亮度Y-p之间的差来设计像素q的权重wl（q），由

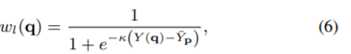
 其中，k控制亮度权重函数的灵敏度。请注意，随着亮度Y（q）变得更亮（，q更可能是雨点像素，因此分配了更大的权重wl（q）。（Y（q）和Y-p的差值是个负数，q是不知道位置的某点的像素，当差值变小，整个式子w1（q）的值相应的变大）

第二个是距离权重wd（q），它被定义为与窗口内q和中心像素p之间的距离成反比，

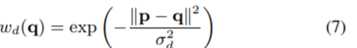
 其中σd=3。如果像素q在空间上更接近中心像素p，我们给它分配一个更大的权重，这是因为，如果两个像素相距很远，它们就不太可能属于同一条雨带。其中exp代表以e为底的指数

第三个是颜色权重wc（q），定义为

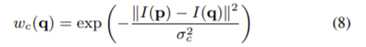
其中σc在本工作中设为9。此权重假定雨纹中的像素具有相似的颜色。因此，wc（q）变得更大，因为q的颜色向量更类似于中心像素p的颜色向量。（该式子的设计和7类似）

此处I（p）和I（q）表示像素p和q的颜色。

我们通过组合（6），（7）和（8）中的三个权重来确定总权重w（q），（受到3个特征的影响）

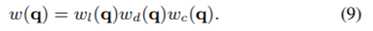
 由于上面说（2）∼（5）中的核回归方法可能会受到窗口内其他图像结构（例如对象边缘）的不利影响。因此为了代替（2），我们得到了修正的协方差矩阵

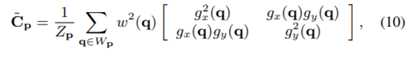
 这里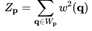。因此，雨像素比无雨像素对修正协方差矩阵的贡献更大。然后，将奇异值分解法应用于修正的协方差矩阵C~p，得到式子4中的旋转角θp和式子5中的标度参数λp和μp 。然后，假设雨痕的形状是垂直方向的高度拉长椭圆，我们检测雨痕。定义了二值雨带图M，如果p是雨点，M（p）=1，否则M（p）=0。当满足以下三个条件时，像素p被宣布为下雨，即M（p）=1。

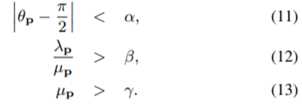
 根据经验，阈值设置为α=π/6、β=2和γ=10。（11）中的第一个条件表示雨带应具有垂直方向。（12）和（13）中的第二和第三个条件表明，雨带应具有细长的椭圆形，并且在长轴和短轴方向上也应突出具有大的特征值。λp和μp表示主轴和主轴方向上的核尺度

完成了对雨的检测的，下面的公式都是针对于如何去雨的：雨带的自适应去除

采用（1）中的非局部均值滤波方法去除检测到的雨滴条纹。虽然Buades等人的去噪算法[8]将非局部均值滤波器应用于图像中的所有像素，但在所提出的算法中，我们仅对M（p）=1的雨点像素p进行滤波。此外，在（1）中，非局部邻域q的权重由Bp和Bq之间的平方距离由确定。然而，当Bp或Bq含有雨带时(Bp、Bq是检测窗口，该窗口里包含多个像素点)，平方距离可能无法如实地传递两个块之间的相似信息。换言之，即使两个块彼此相似，由于雨痕，平方距离也可能很大。因此，我们将Bp和Bq中的雨点像素排除在权重计算之外。让Rp和Rq表示二元列向量（即该列向量中包含两个元素），它们分别对应于雨带图中以p和q为中心的块。然后，在（1）中，我们使用修改后的向量代替Bp 和Bq

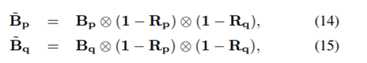
其中，运算符⊗表示两个向量之间的元素相乘，1是所有元素都为1的列向量。

然后，我们使用自适应非局部均值滤波器将雨点像素p替换为Iˆ（p），由

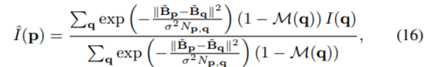
 其中，Np，q是向量（1-Rp）⊗（1-Rq）中非零元素的数目。换句话说，Np，q计算像素位置，其中Bp和Bq都有无雨像素。

请注意，（16）中的术语（1-M（q））也用于避免将雨点像素用作非本地相邻像素。解释如下：M（q）的作用根据上面所说即是检测像素点q，当像素点q处于雨条纹带时，M（q）的值为1；而在式子16中，若q处于雨条纹中时，由于（1-M（q））则其不会算入加权中而是直接忽略，这样在进均值滤波的时候便能跳过大部分的雨区域。

补充理解：

非局部均值滤波：

　　非局部均值（NL-means）是近年来提出的一项新型的去噪技术。该方法充分利用了图像中的冗余信息，在去噪的同时能最大程度地保持图像的细节特征。基本思想是：当前像素的估计值由图像中与它具有相似邻域结构的像素加权平均得到。

　　奇异值可以被看作成一个矩阵的代表值，或者说，奇异值能够代表这个矩阵的信息。当奇异值越大时，它代表的信息越多。因此，我们取前面若干个最大的奇异值，就可以基本上还原出数据本身。

SINGLE-IMAGE DERAINING USING AN ADAPTIVE NONLOCAL MEANS FILTER论文分析（以公式分析为主导）

标签：bsp   条纹   运算   中心   back   恢复   缩放   计算   经验   

原文地址：https://www.cnblogs.com/xwh-blogs/p/12686456.html