标签:nod || 现在 node 引用 inf 读取 解决 调用函数
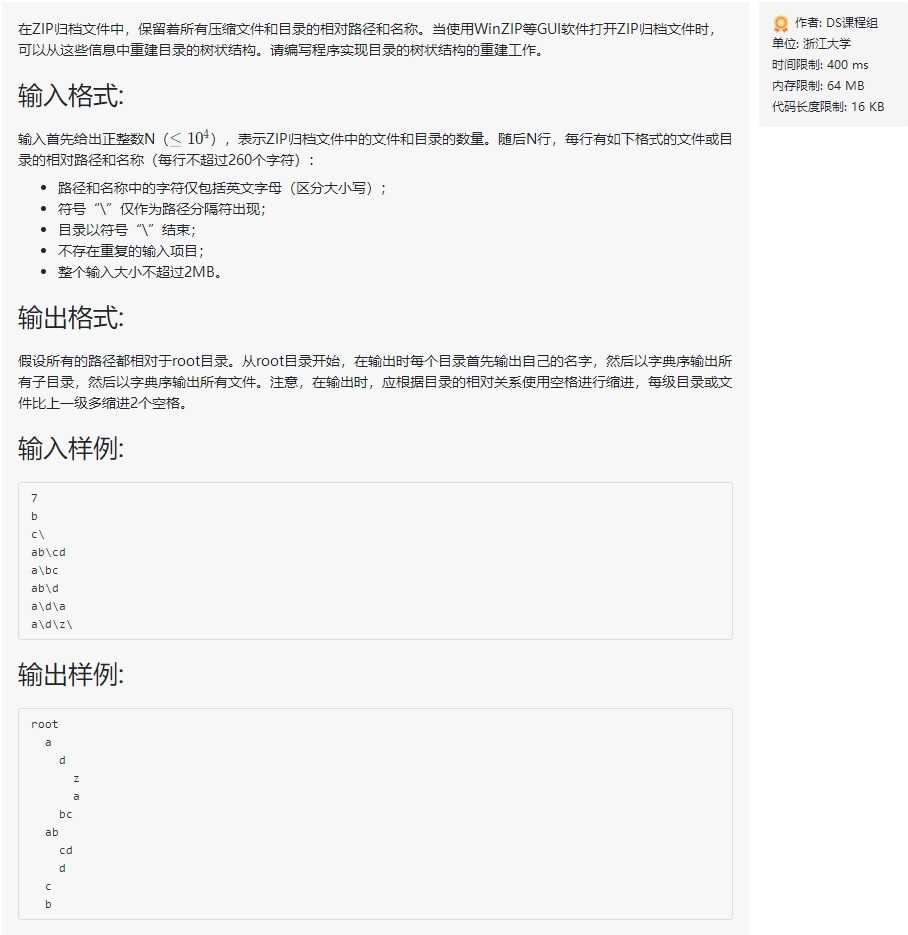
看到这个问题,我们是一头雾水啊,这讲了个啥?别急,让我们用测试样例模拟一遍。
首先我们先考虑存储数据的方式,根据观察和我们对文件夹的理解,对于一个文件夹而言,与其他文件或文件夹只会有 2 种关系——和我在同一目录、在我的目录,也就是只有同级和下级两种关系。因此我们就很自然地想到孩子兄弟表示法,因为在孩子兄弟对于一个结点也只会有 2 种关系——孩子和兄弟,那我们就用孩子表示在下级目录,兄弟表示在同级目录。
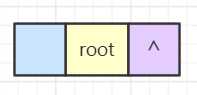
首先我们拥有一个根目录 root,读取第一行数据,表示根目录有个名为 b 的文件,是 root 的孩子,因此根据孩子兄弟表示法,b 应该是 root 的左分支结点。
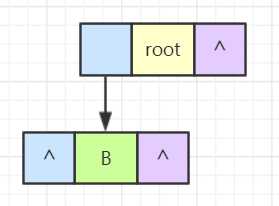
读取第二行数据,在根目录中有个 c 目录。因此 c 目录是 root 的孩子,并且与 b 文件同级,也就是互为兄弟关系,进行结点的加入。
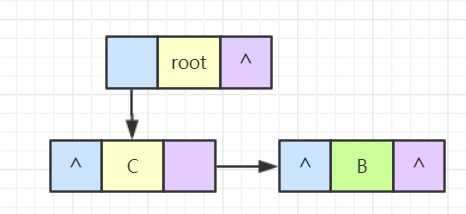
读取第三行数据,在根目录中有个 ab 目录,并在这个目录下有个 cd 文件。因此 ab 目录是 root 的孩子,并且与 c 目录同级,也就是互为兄弟关系,同时 ab 目录有个左分支 cd,进行结点的加入。
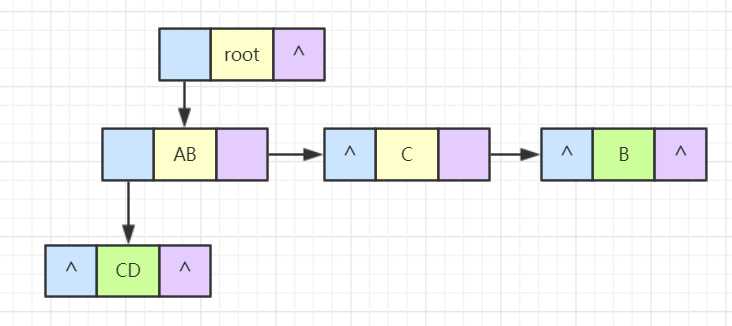
读取第四行数据,在根目录中有个 a 目录,并在这个目录下有个 bc 文件。因此 a 目录是 root 的孩子,并且与 ab 目录同级,也就是互为兄弟关系,同时 a 目录有个左分支 bc,进行结点的加入。
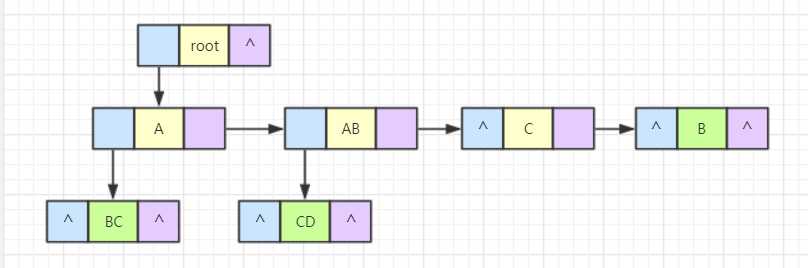
读取第五行数据,在 ab 目录下有个 d 文件。由于 ab 已经存在,因此 d 与 cd 互为兄弟关系,修改 ab 的孩子为 d,d 的兄弟为 cd,进行结点的加入。
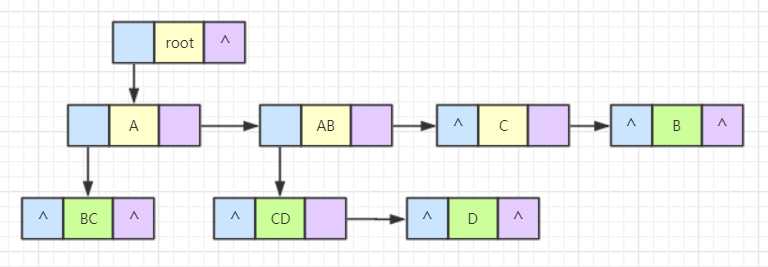
重复上述操作完成建树。
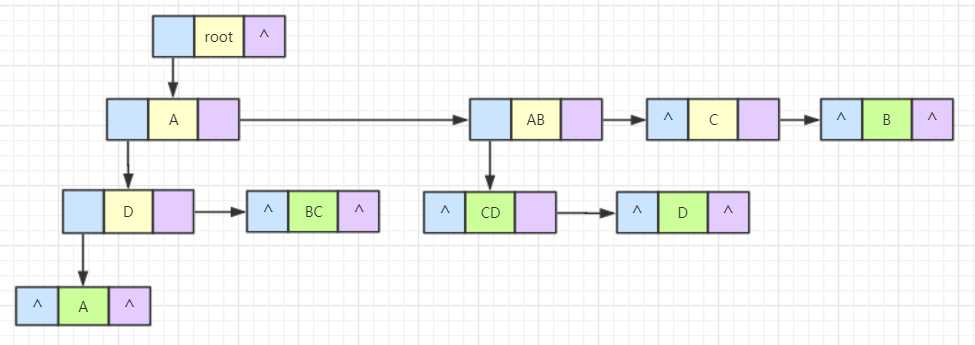
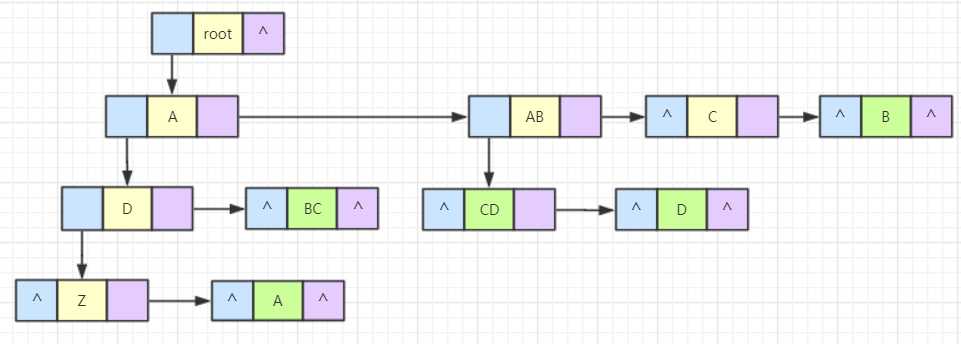
把这棵树整理成二叉树的形式。
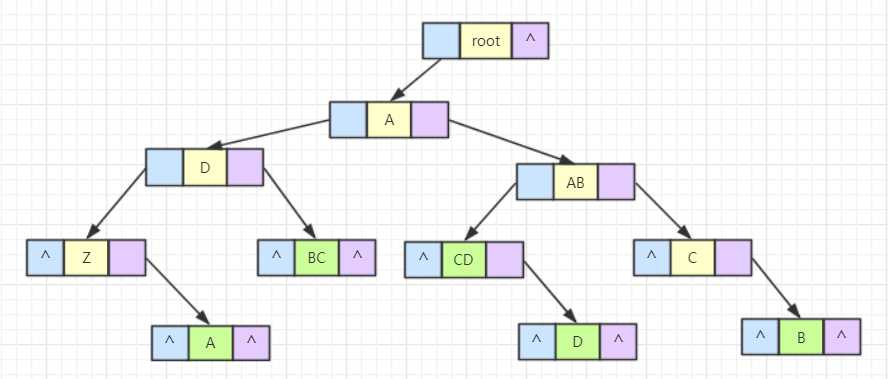
我们按照前序遍历的顺序读一下这课树,发现在忽略缩进的情况下,读取的顺序和样例的输出数据是一模一样啊,也就是说,只要把这棵树建出来,这个情景我们就解决了。在应用的时候,我们应当积极地考虑使用孩子兄弟表示法建树,因为这种方法建立的是二叉树,我们就可以用二叉树的基操来操作这棵树。
typedef struct CSNode
{
string data; //数据域
struct CSNode* firstchild; //指向对应长子结点的指针域
struct CSNode* rightsib; //指向对应右兄弟结点的指针域
int flag_file; //判断是文件还是目录的 flag
}CSNode, * CSTree;
切片算法可以用字符数组实现,也可以用 string 类实现,此处我用字符数组描述。由于我们读入的数据是字符串,因此我们需要先把各个目录分离开来。需要注意的是,虽然文件是特殊数据,但是文件只会出现在字符串串尾,因此只需要一个分支结构单独处理即可。

需要强调的是,string?类用来判断字典序和复制操作都可以直接用运算符实现,更为方便。
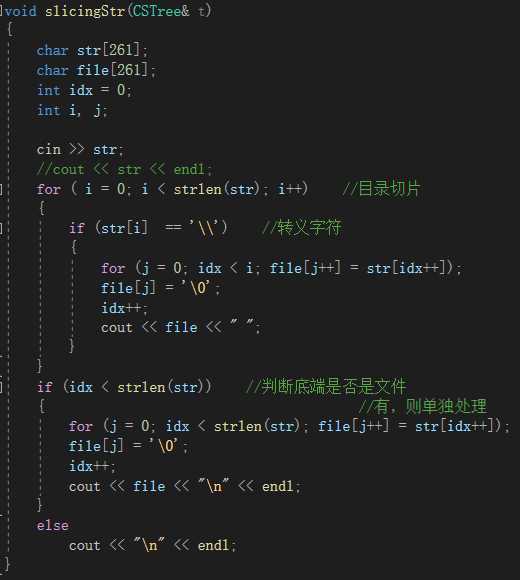

建树算法只需要再字符串切片算法进行改动即可,把输出语句改为调用结点插入函数即可实现。

void createTree(CSTree pre, string str)
{
int idx = 0;
getline(cin, str);
for (int i = 0; i < str.size(); i++)
{
if (str[i] == ‘\\‘) //注意用反义字符,不然会报错
{ //只要不在串尾,只会是目录
pre = insertNode(pre, str.substr(idx, i - idx), 1);
idx = i + 1; //移动字符串到下一个目录,即 ‘\‘ 之后
}
}
if (idx < str.size()) //文件只出现在字符串尾
{
pre = insertNode(pre, str.substr(idx, str.size() - idx), 0);
}
}
该算法的目的是向一个树结构中,在正确的位置插入新结点,是解决这个问题的核心。这里要强调一下返回值的重要性,如果不设置返回值,而是把目录引用进去,那么回到调用函数的时候需要自行将指针移动到当前目录,更为繁琐,好的解法是将插入后的接点作为所在的目录,以此为返回值返回函数调用的位置。容易出错的地方是若插入位置是目录的长子结点的话,直接通过前驱指针的后继来操作会插在错误位置导致断链,因此需要设置当前位置指针和前驱指针,就可以规避这个问题。

CSTree insertNode(CSTree t, string str, int flag) //解决问题的核心
{
CSTree a_node = new CSNode;
CSTree pre = t, ptr;
a_node->data = str; //初始化新结点
a_node->firstchild = a_node->rightsib = NULL;
a_node->flag_file = flag;
if (t->firstchild == NULL) //所在目录没孩子,直接插入结点
{
t->firstchild = a_node;
return t->firstchild;
}
ptr = t->firstchild; //由于根结点本身插入时,是插在长子位,因此另外设置 pre 当前驱结点,ptr 当 pre 的后继
while (ptr != NULL && ((ptr->flag_file > a_node->flag_file) || (ptr->flag_file == a_node->flag_file && str > ptr->data)))
{
pre = ptr;
ptr = ptr->rightsib; //同时移动 ptr 和其前驱,这么做的好处是不需要考虑长子结点和兄弟结点的关系
}
//要先判空,不然有段错误
if (ptr == NULL) //无处可插入,插在链尾
{
a_node->rightsib = pre->rightsib;
pre->rightsib = a_node;
return a_node; //接下来以 a_node 为根目录操作
}
else if (ptr->data == a_node->data && ptr->flag_file == a_node->flag_file) //目录或文件已存在(之前因为这个出了 bug)
{
delete a_node; //把申请的新结点打掉
return ptr; //接下来在已有的 ptr 目录下操作
}
else //找到了应该插入的位置
{
if (pre->data == t->data) //插在根目录的长子位
{
a_node->rightsib = pre->firstchild;
pre->firstchild = a_node;
}
else //正常插入
{
a_node->rightsib = pre->rightsib;
pre->rightsib = a_node;
}
return a_node; //接下来以 a_node 为根目录操作
}
}
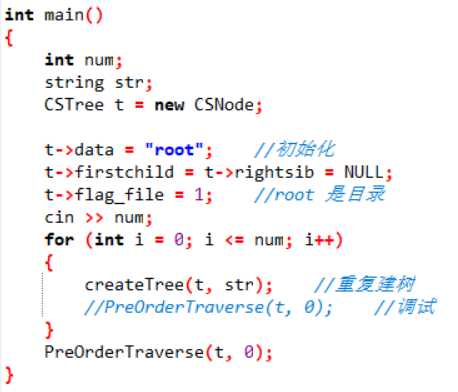
我们已经知道输出结点的顺序就是先序遍历二叉树的顺序,因此我们只需要添加个缩进的机制就能实现。
void PreOrderTraverse(CSTree T, int space)
{ //因为要输出空格,稍微改装遍历算法
if (T == NULL)
return;
for (int i = 0; i < space; i++)
{
cout << " ";
}
cout << T->data << endl; //前序遍历
PreOrderTraverse(T->firstchild, space + 2); //下一层多两个空格
PreOrderTraverse(T->rightsib, space); //兄弟结点不需要多空格
}
15
b
cab\cd
a\bc
ab\d
a\d\a
a\d\zbc
ab\cd\e
a\bc\f
ab\d\g
a\d\a\h
a\d\z
root
a
bc
f
d
a
h
z
a
z
bc
ab
cd
e
d
g
cd
d
b
c
b
c
标签:nod || 现在 node 引用 inf 读取 解决 调用函数
原文地址:https://www.cnblogs.com/linfangnan/p/12617499.html