标签:如何 返回值 局限性 value 最小值 不难 理解 表格 问题
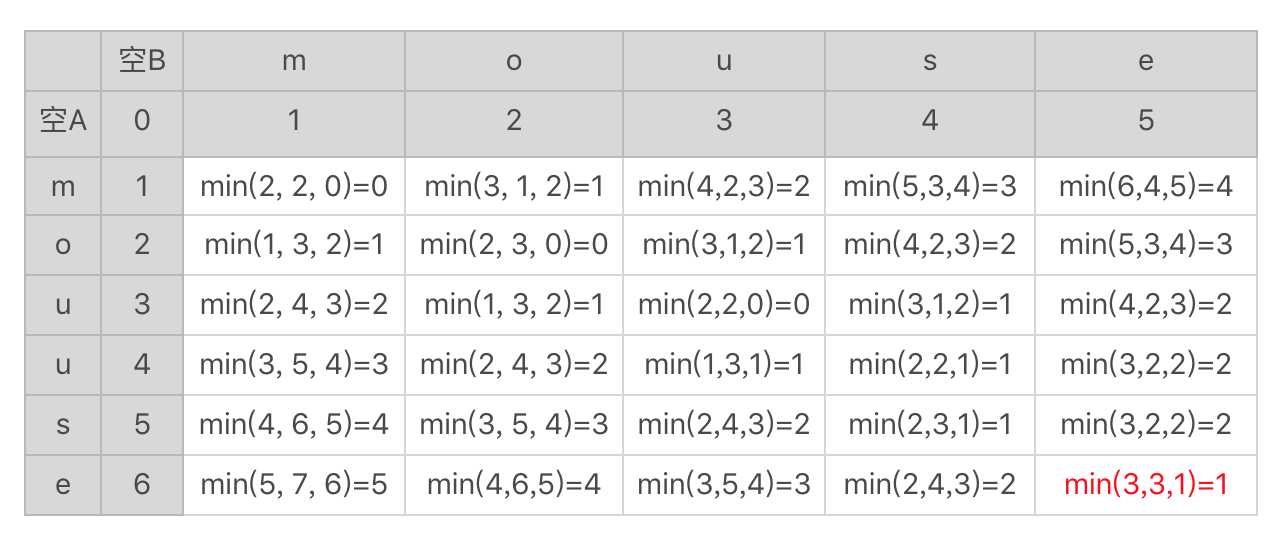
这里面求最小值的 min 函数里有三个参数,分别对应我们上节讲的三种情况的编辑距离,分别是:替换、插入和删除字符。在表格的右下角标出了两个字符串的编辑距离 1。
我们假设字符数组 A[]和 B[]分别表示字符串 A 和 B,A[i]表示字符串 A 中第 i 个位置的字符,B[i]表示字符串 B 中第 i 个位置的字符。二维数组 d[,]表示刚刚用于推导的二维表格,而 d[i,j]表示这张表格中第 i 行、第 j 列求得的最终编辑距离。函数 r(i, j) 表示替换时产生的编辑距离。如果 A[i]和 B[j]相同,函数的返回值为 0,否则返回值为 1。
这里面最关键的一步是 d[i, j]=min(d[i-1, j] + 1, d[i, j-1] + 1, d[i-1, j-1] + r(i, j))。这个表达式表示的是动态规划中从上一个状态到下一个状态之间可能存在的一些变化,以及基于这些变化的最终决策结果。我们把这样的表达式称为状态转移方程。
有了状态转移方程,我们就可以很清晰地用数学的方式,来描述状态转移及其对应的决策过程,而且,有了状态转移方程,具体的编码其实就很容易了。
如果我们使用动态规划法来实现编辑距离的测算,那就能确保查询推荐的效率和效果。不过,基于编辑距离的算法也有局限性,它只适用于拉丁语系的相似度衡量,所以通常只用于英文或者拼音相关的查询。如果是在中文这种亚洲语系中,差一个汉字(或字符)语义就会差很远,所以并不适合使用基于编辑距离的算法。
给定总金额和可能的钱币面额,能否找出钱币数量最少的奖赏方式?
假设这里我们有三种面额的钱币,2 元、3 元和 7 元。为了凑满 100 元的总金额,我们有三种选择。
第一种,总和 98 元的钱币,加上 1 枚 2 元的钱币。如果凑到 98 元的最少币数是 x_{1},那么增加一枚 2 元后就是 (x_{1} + 1) 枚。
第二种,总和 97 元的钱币,加上 1 枚 3 元的钱币。如果凑到 97 元的最少币数是 x_{2},那么增加一枚 3 元后就是 (x_{2} + 1) 枚。
第三种,总和 93 元的钱币,加上 1 枚 7 元的钱币。如果凑到 93 元的最少币数是 x_{3},那么增加一枚 7 元后就是 (x_{3} + 1) 枚。
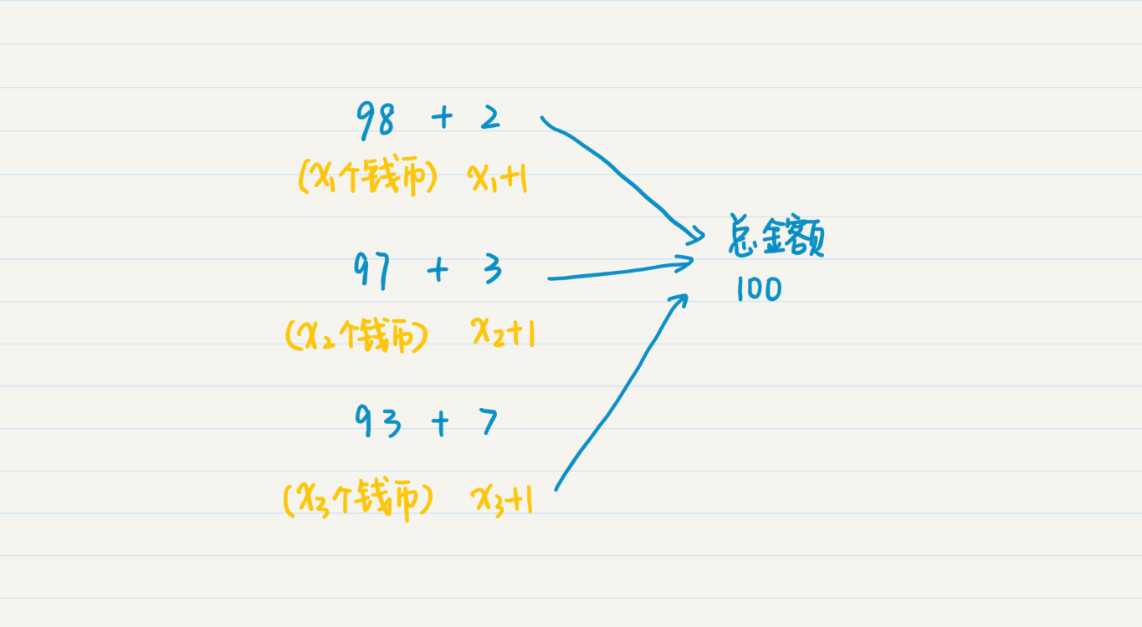
比较一下以上三种情况的钱币总数,取最小的那个就是总额为 100 元时,最小的钱币数。换句话说,由于奖赏的总金额是固定的,所以最后选择的那枚钱币的面额,将决定到上一步为止的金额,同时也决定了上一步为止钱币的最少数量。根据这个,我们可以得出如下状态转移方程:
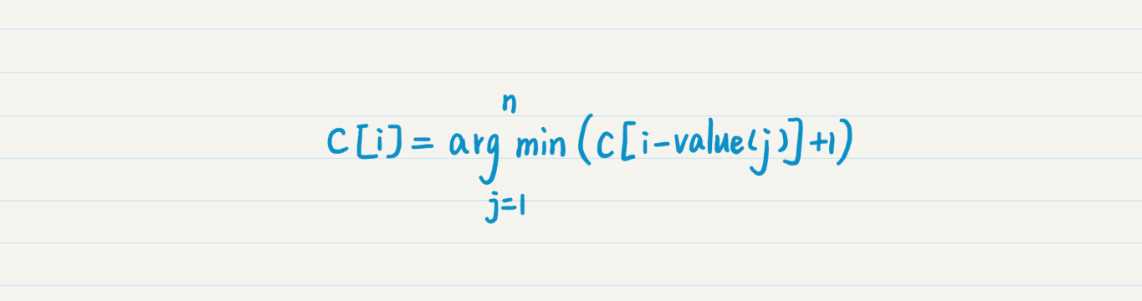
其中,c[i]表示总额为 i 的时候,所需要的最少钱币数,其中 j=1,2,3,…,n,表示 n 种面额的钱币,value[j]表示第 j 种钱币的面额。c[i - values(j)]表示选择第 j 种钱币的时候,上一步为止最少的钱币数。需要注意的是,i - value(j) 需要大于等于 0,而且 c[0] = 0。
表格每一行表示奖赏的总额,前 3 列表示 3 种钱币的面额,最后一列记录最少的钱币数量。表中的“/”表示不可能,或者说无解。
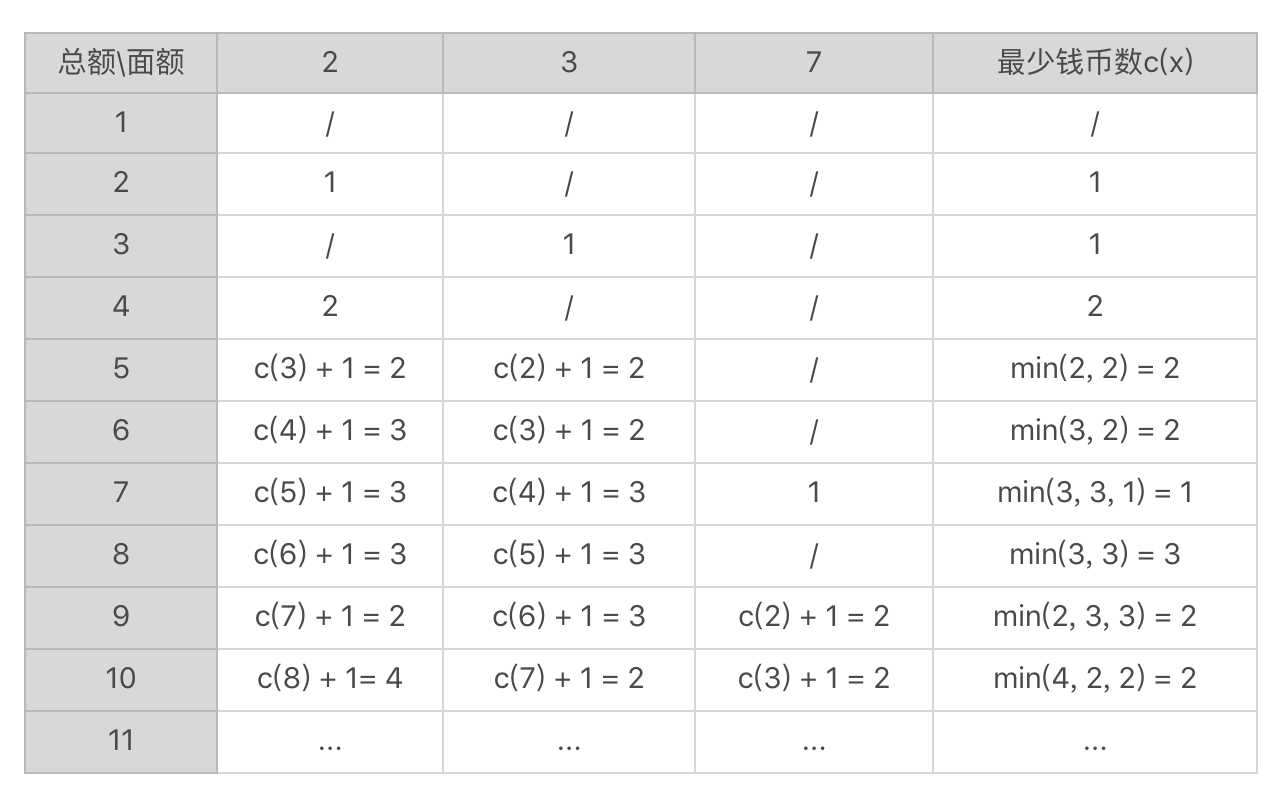
这张状态转移表同样可以帮助你来理解状态转移方程的正确性。一旦状态转移方程确定了,要编写代码来实现就不难了。
首先,如果一个问题有很多种可能,看上去需要使用排列或组合的思想,但是最终求的只是某种最优解(例如最小值、最大值、最短子串、最长子串等等),那么你不妨试试是否可以使用动态规划。
其次,状态转移方程是个关键。你可以用状态转移表来帮助自己理解整个过程。如果能找到准确的转移方程,那么离最终的代码实现就不远了。当然,最好的方式,还是结合工作中的项目,不断地实践,尝试,然后总结。

标签:如何 返回值 局限性 value 最小值 不难 理解 表格 问题
原文地址:https://www.cnblogs.com/liugangjiayou/p/12689590.html