标签:拆分 mes 个数 tin alt time 失败 lag weight
题外话:
这场的\(D\)题印象深刻。。。太骚了
还好没打,不然刚上的黄又白给。。。
还有\(boboniu\)和\(MiFaFa\)都莫了/kk悲/kk
题意
一个序列\(a\),在第\(x\)时刻你可以选择任意多项\(a_i\)使他们同时加\(2^{x-1}\),问使得这个序列变成非降最少需要多少时间。
题解
显然每个数只要达到前面最大数的值就好了。
Code
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define Mp make_pair
#define pb push_back
using ll = long long;
using db = double;
using pii = pair<int, int>;
using vi = vector<int>;
const int N = 1e5 + 100;
int _, n, a[N], ans;
signed main(){
for(scanf("%d", &_); _; _--) {
scanf("%d", &n); ans = 0;
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
for(int i = 1, mx = a[1]; i <= n; i++)
ans = max(ans, mx - a[i]), mx = max(mx, a[i]);
// printf("ans:%d\n", ans);
for(int i = 30; i >= 0; i--) {
if(ans >> i & 1) {
printf("%d\n", i + 1);
break;
}
}
if(ans == 0) puts("0");
}
fprintf(stderr, "time=%.4f\n", (db)clock()/CLOCKS_PER_SEC);
return 0;
/* 取模直接除,爆零两行泪
* 不开ll见祖宗
*/
}
Ps:
考场上没构造出来的说。。。
题意
一棵树给边加权,使得每对叶子节点之间的路径上的边的\(Xor\)和为\(0\),问权值集合的最小大小和最大大小(去重)。
题解
Min:
主要思路:纯属构造。
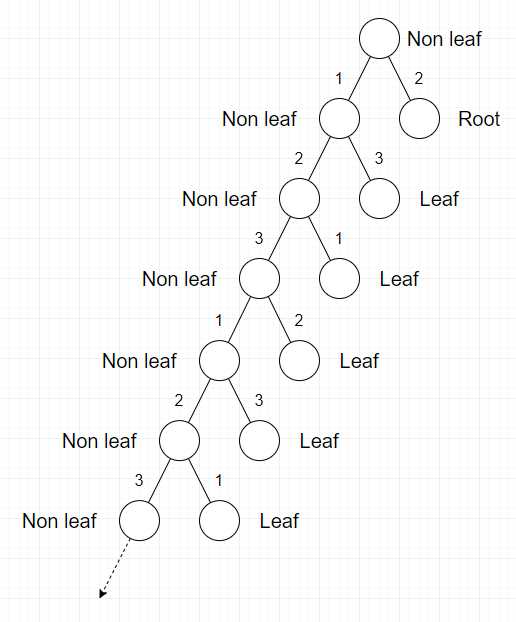
这么构造可以证明最小值不超过\(3\)。
当你选取任意一个节点为根时,如果所有的叶子节点都在同一奇偶性的层数上(即任意两对叶子节点间的路径长度都是偶数)时,我们显然可以把所有边都赋为同一个值,答案为1。
Max:
主要思路:当你选取了一个是叶子节点的根节点后,任意两对叶子之间的路径都可以拆分成两条路径\(u\rightarrow rt,v\rightarrow rt\),那么我们只需要保证这两条路径都为\(0\)即可,至于重复的部分显然,没有影响。
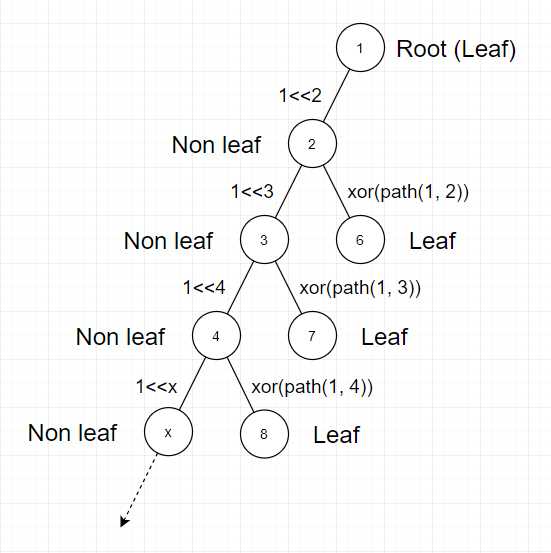
如图所示,我们选取一个叶子节点作为根节点,对于所有的非叶子节点\(i\),\(2^x\rightarrow(i,fa_i)\),对于所有的叶子节点\(i\),\(xor(path(root,p_I))\rightarrow(i,fa_i)\),这样构造可以达到最大值,那么不难发现最后的答案是\(e-l+m\),其中\(e\)为边总数,\(l\)为叶子节点总数,\(m\)为非叶子节点但有叶子儿子的节点总数,\(dfs\)一遍即可。
或者你直接做一个\(dp\),\(f_i=\sum_{j\in Son_i\&\&j\ isn‘t\ a\ leaf}(f_j+1) + [i\ has\ a\ leaf]\),答案就是\(f_{rt}\),\(rt\)任意选取。
Code
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define Mp make_pair
#define pb push_back
using ll = long long;
using db = double;
using pii = pair<int, int>;
using vi = vector<int>;
const int N = 1e5 + 100;
int n, v[N]; vi G[N];
bool chk(int rt) {
queue<int> q; q.push(rt); v[rt] = 1;
while(q.size()) {
int x = q.front(); q.pop();
for(int y : G[x]) if(!v[y])
v[y] = v[x] + 1, q.push(y);
}
for(int i = 1, lst = -1; i <= n; i++)
if(G[i].size() == 1) {
if(i == rt) continue;
if(lst == -1) {lst = v[i]; continue;}
if(lst % 2 != v[i] % 2) return false;
lst = v[i];
}
return true;
}
int dfs(int x, int fz) {
int ret = 0, flag = 0;
for(int y : G[x]) if(y != fz) {
if(G[y].size() != 1) ret += dfs(y, x) + 1;
else flag = 1;
}
return ret + flag;
}
signed main(){
scanf("%d", &n);
for(int i = 1; i < n; i++) {
int x, y; scanf("%d %d", &x, &y);
G[x].pb(y), G[y].pb(x);
} int rt = 1, mx = 0;
for(int i = 1; i <= n; i++) if(G[i].size() > mx) rt = i, mx = G[i].size();
printf("%d %d\n", chk(rt) ? 1 : 3, dfs(rt, 0));
fprintf(stderr, "time=%.4f\n", (db)clock()/CLOCKS_PER_SEC);
return 0;
/* 取模直接除,爆零两行泪
* 不开ll见祖宗
*/
}
Ps:
打表万岁,找规律万岁,小学奥数题万岁。
但是不得不说这题正解找规律真的屑。
题意
你要按照如下方法构造一个序列\(s\)。
找到字典序最小的三元组\((a,b,c)\)满足以下条件:
\(a\oplus b\oplus c=0\)
\(a,b,c\)不在\(s\)中
将它们按序插入\(s\),循环。
问\(s_i,i\le10^{16}\)。
题解
通过打表可以发现第一列递增,第二列和第三列其实是一个关于\(4\)的在二进制意义下的循环序列,或者你可以把它理解为先转成\(4\)进制,然后将\(4\)进制转为\(2\)进制,只不过\(4\rightarrow2\)的映射关系被改变了。
64 128 192 0 0 0 0000 0000
65 130 195 1 2 3 0010 0011
66 131 193 2 3 1 0011 0001
67 129 194 3 1 2 0001 0010
68 136 204 4 8 12 1000 1100
69 138 207 5 10 15 1010 1111
70 139 205 6 11 13 1011 1101
71 137 206 7 9 14 1001 1110
72 140 196 8 12 4 1100 0100
73 142 199 9 14 7 1110 0111
74 143 197 10 15 5 1111 0101
75 141 198 11 13 6 1101 0110
76 132 200 12 4 8 0100 1000
77 134 203 13 6 11 0110 1011
78 135 201 14 7 9 0111 1001
79 133 202 15 5 10 0101 1010
80 160 240 16 32 48 .... ....
81 162 243 17 34 51
82 163 241 18 35 49
83 161 242 19 33 50
84 168 252 20 40 60
85 170 255 21 42 63
86 171 253 22 43 61
87 169 254 23 41 62
88 172 244 24 44 52
89 174 247 25 46 55
90 175 245 26 47 53
91 173 246 27 45 54
92 164 248 28 36 56
93 166 251 29 38 59
94 167 249 30 39 57
95 165 250 31 37 58
96 176 208 32 48 16
97 178 211 33 50 19
98 179 209 34 51 17
99 177 210 35 49 18
100 184 220 36 56 28
101 186 223 37 58 31
102 187 221 38 59 29
103 185 222 39 57 30
104 188 212 40 60 20
105 190 215 41 62 23
106 191 213 42 63 21
107 189 214 43 61 22
Code
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define Mp make_pair
#define pb push_back
using ll = long long;
using db = double;
using pii = pair<int, int>;
using vi = vector<int>;
signed main(){
// freopen("data.in", "r", stdin);
// freopen("std.out", "w", stdout);
int _;
for(scanf("%d", &_); _; _--) {
ll n;
scanf("%lld", &n);
ll pw4 = 4, pre = 0;
while(pw4 <= n) pre += pw4 / 4, pw4 *= 4;
ll segl = pw4 / 4, segr = pw4; pw4 /= 4;
//[segl, segr)
ll lie = (n - 1) % 3 + 1, hang = (n + 2) / 3 - pre;
// 所在列数 所在当前块中的行数
if(lie == 1) {
printf("%lld\n", segl + hang - 1);
} else if(lie == 2) {
ll v[4] = {0, 2, 3, 1};
ll del = 0; hang--;
for(int i = 0; hang; i += 2, hang /= 4) del += v[hang % 4] << i;
printf("%lld\n", segl + pw4 + del);
} else {
ll v[4] = {0, 3, 1, 2};
ll del = 0; hang--;
for(int i = 0; hang; i += 2, hang /= 4) del += v[hang % 4] << i;
printf("%lld\n", segl + pw4 + pw4 + del);
}
}
fprintf(stderr, "time=%.4f\n", (db)clock()/CLOCKS_PER_SEC);
return 0;
/* 取模直接除,爆零两行泪
* 不开ll见祖宗
*/
}
打表Code
#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define Mp make_pair
#define pb push_back
using ll = long long;
using db = double;
using pii = pair<int, int>;
using vi = vector<int>;
int mex(set<int> st1, set<int> st2) {
for(int i = 1; ; i++) if(st1.find(i) == st1.end() && st2.find(i) == st2.end()) return i;
}
int ch(int x) {
int pw4 = 1;
while(pw4 <= x) pw4 *= 4;
pw4 /= 4;
while(x >= pw4) x -= pw4;
return x;
}
signed main(){
freopen("my.out", "w", stdout);
set<int> st; vi now;
for(int i = 1; i <= 500; i = mex(st, {})) {
set<int> st2 = {i};
for(int j = mex(st, st2); j; st2.insert(j), j = mex(st, st2))
if(st.find(i ^ j) == st.end()) {
printf("%4d %4d %4d %4d %4d %4d\n", i, j, (i ^ j), ch(i), ch(j), ch(i ^ j));
now.pb(i), now.pb(j), now.pb(i ^ j);
st.insert(i), st.insert(j), st.insert(i ^ j);
break;
}
}
// for(int i : now) printf("%4d ", i); puts("");
fprintf(stderr, "time=%.4f\n", (db)clock()/CLOCKS_PER_SEC);
return 0;
/* 取模直接除,爆零两行泪
* 不开ll见祖宗
*/
}
Ps:
这题好草啊,谁\(tmd\)想出这种题目的,脑回路看\(8\)透。
\(boboniu\)他倒下了,他倒在了这题上,他狙击\(tourist\)失败了,悲。
题意
一棵树转化为多边形,节点间有边则多边形有交,问多边形最大深度(即最多嵌套几层)。
题解
咕咕咕
Code
咕咕咕
题意
咕咕咕
题解
咕咕咕
Code
咕咕咕
标签:拆分 mes 个数 tin alt time 失败 lag weight
原文地址:https://www.cnblogs.com/JHDHJjuruo/p/12690414.html