标签:csdn 接下来 with rop 相对 containe stat __add__ ima
@
@article{das2011differential,
title={Differential Evolution: A Survey of the State-of-the-Art},
author={Das, Swagatam and Suganthan, P N},
journal={IEEE Transactions on Evolutionary Computation},
volume={15},
number={1},
pages={4--31},
year={2011}}
这是一篇关于Differential Evolution (DE) 的综述, 由于对这类方法并不熟悉, 只能简单地做个记录.
考虑如下问题,
其中\(X=(x_1,\ldots,x_D)\).
我所知的, 如梯度下降方法, 贝叶斯优化可以用来处理这类问题, 但是还有诸如 evolutionary algorithm (EA), evolutionary programming (EP), evolution strategies(ESs), genetic algorithm (GA), 以及本文介绍的 DE (后面的基本都不了解).
先给出最初的形式, 称之为DE/rand/1/bin:
Input: scale factor \(F\), crossover rate \(Cr\), population size \(NP\).
1: 令\(G=0\), 并随机初始化\(P_G=\{ X_{1,G},\ldots, X_{NP,G}\}\).
2: While the stopping criterion is not satisfied Do:
其中\(X_{i,G}=(x_{j,i,G}, \ldots, x_{D,i,G})\), \(j_{rand}\)是预先随机生成的一个属于\([1,D]\)的整数, 以保证\(U\)相对于\(X\)至少有些许变化产生, \(X_{r_1^i,G}, X_{r_2^i,G},X_{r_3^i,G}\)是从\(P_G\)中随机抽取且互异的.
在接下来我们可以发现很多变种, 而这些变种往往是Mutation step 和 Crossover step的变体.
这是crossover step步的的一个变种:
随机从\([1, D]\)中抽取整数\(n\)和\(L\), 然后
\(L\)可以通过下面的步骤生成
其中\(X_{best,G}\)是\(P_{G}\)中的最优的点.
真的没有细看, 文中粗略地介绍了几处, 还有很多需要查原文.
有的推荐\([0.4, 1]\)(最佳0.5), 有的推荐\(0.6\), 有的推荐\([0.4, 0.95]\)(最佳0.9).
还有一些自适应的选择, 如
我比较疑惑的是难道\(|\frac{f_{\max}}{f_{\min}}|\)不是大于等于1吗?
其中\(F_l\), \(F_u\)分别为\(F\)取值的下界和上界.
有的推荐\([5D,10D]\), 有的推荐\([3D, 8D]\).
有的推荐\([0.3, 0.9]\).
还有
如果\(\mathrm{rand}[0,1] < \Gamma\)(\(\Gamma\)是给定的):
否则
其中\(k_i\)给定, \(F‘=k_i \cdot F\).
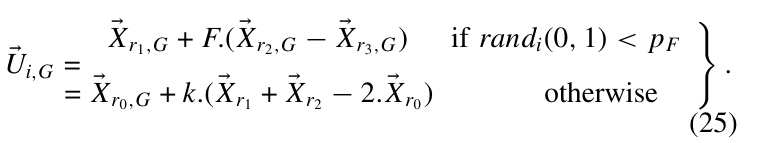
即在考虑\(x\)的时候, 还需要考虑其反\(a+b-x\), 假定\(x \in [a, b]\), \([a,b]\)为我们给定范围, \(X\)的反类似的构造.
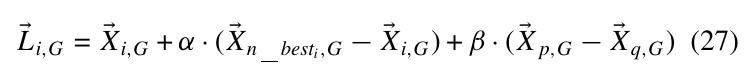
其中\(X_{n_{best},G}\)表示在\(X_{i,G}\)的\(n\)的近邻中的最优点, \(p, q\in [i-k,i+k]\).
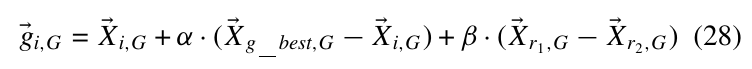
其中\(X_{g_{best},G}\)为\(P_G\)中的最优点.
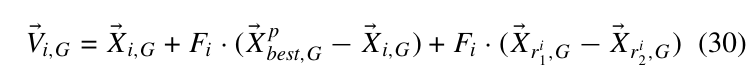
剩下的在复杂环境下的应用就不记录了(只是单纯讲了该怎么做).
\(f(x,y)=x^2+50y^2\).
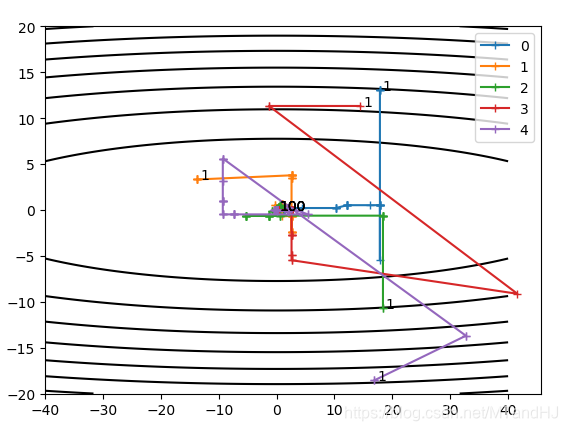
{
"dim": 2,
"F": 0.5,
"NP": 5,
"Cr": 0.35
}
"""
de.py
"""
import numpy as np
from scipy import stats
import random
class Parameter:
def __init__(self, dim, xmin, xmax):
self.dim = dim
self.xmin = xmin
self.xmax = xmax
self.initial()
def initial(self):
self.para = stats.uniform.rvs(
self.xmin, self.xmax - self.xmin
)
@property
def data(self):
return self.para
def __getitem__(self, item):
return self.para[item]
def __setitem__(self, key, value):
self.para[key] = value
def __len__(self):
return len(self.para)
def __add__(self, other):
return self.para + other
def __mul__(self, other):
return self.para * other
def __pow__(self, power):
return self.para ** power
def __neg__(self):
return -self.para
def __sub__(self, other):
return self.para - other
def __truediv__(self, other):
return self.para / other
class DE:
def __init__(self, func, dim ,F=0.5, NP=50,
Cr=0.35, xmin=-10, xmax=10,
require_history=True):
self.func = func
self.dim = dim
self.F = F
self.NP = NP
self.Cr = Cr
self.xmin = np.array(xmin)
self.xmax = np.array(xmax)
assert all(self.xmin <= self.xmax), "Invalid xmin or xmax"
self.require_history = require_history
self.init_x()
if self.require_history:
self.build_history()
def init_x(self):
self.paras = [Parameter(self.dim, self.xmin, self.xmax)
for i in range(self.NP)]
@property
def data(self):
return [para.data for para in self.paras]
def build_history(self):
self.paras_history = [self.data]
def add_history(self):
self.paras_history.append(self.data)
def choose(self, size=3):
return random.sample(self.paras, k=size)
def mutation(self):
x1, x2, x3 = self.choose(3)
return x1 + self.F * (x2 - x3)
def crossover(self, v, x):
u = np.zeros_like(v)
for i, _ in enumerate(v):
jrand = random.randint(0, self.dim)
if np.random.rand() < self.Cr or i is jrand:
u[i] = v[i]
else:
u[i] = x[i]
u[i] = v[i] if np.random.rand() < self.Cr else x[i]
return u
def selection(self, u, x):
if self.func(u) < self.func(x):
x.para = u
else:
pass
def step(self):
donors = [self.mutation()
for i in range(self.NP)]
for i, donor in enumerate(donors):
x = self.paras[i]
u = self.crossover(donor, x)
self.selection(u, x)
if self.require_history:
self.add_history()
def multi_steps(self, times):
for i in range(times):
self.step()
class DEbest1(DE):
def bestone(self):
y = np.array([self.func(para)
for para in self.paras])
return self.paras[np.argmax(y)]
def mutation(self, bestone):
x1, x2 = self.choose(2)
return bestone + self.F * (x1 - x2)
def step(self):
bestone = self.bestone()
donors = [self.mutation(bestone)
for i in range(self.NP)]
for i, donor in enumerate(donors):
x = self.paras[i]
u = self.crossover(donor, x)
self.selection(u, x)
if self.require_history:
self.add_history()
class DEbest2(DEbest1):
def mutation(self, bestone):
x1, x2, x3, x4 = self.choose(4)
return bestone + self.F * (x1 - x2) + self.F * (x3 - x4)
class DErand2(DE):
def mutation(self):
x1, x2, x3, x4, x5 = self.choose(5)
return x1 + self.F * (x2 - x3) + self.F * (x4 - x5)
class DErandTM(DE):
def mutation(self):
x = self.choose(3)
y = np.array(list(map(self.func, x)))
p = y / y.sum()
part1 = (x[0] + x[1] + x[2]) / 3
part2 = (p[1] - p[0]) * (x[0] - x[1])
part3 = (p[2] - p[1]) * (x[2] - x[1])
part4 = (p[0] - p[2]) * (x[2] - x[0])
return part1 + part2 + part3 + part4
Differential Evolution: A Survey of the State-of-the-Art
标签:csdn 接下来 with rop 相对 containe stat __add__ ima
原文地址:https://www.cnblogs.com/MTandHJ/p/12695069.html