标签:线性 isp 类别 迭代 最小值 sig img hat mamicode
逻辑回归其实并不“逻辑”也不是回归,而是分类模型,逻辑是指利用了Logistic非线性函数。
在logistic regression中,我们用logistic函数来预测类别标签的后验概率
这里\(x=[x_1,\cdots,x_D,1]\)和\(w=[w_1,\cdots,w_D,b]\),是\(D+1\)维的增广的特征向量和权重向量。
标签\(y=0\)的后验概率
由公式1可以得到
其中\(\frac{p(y=1|x)}{p(y=0|x)}\)称为几率(Odds),所以\(w^Tx\)就是几率的对数,所以逻辑回归也称为对数几率回归。
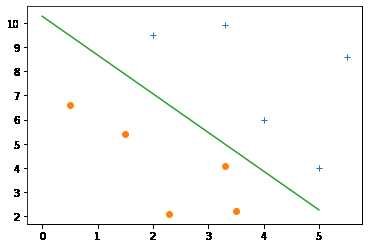
当正负样本概率相等时,\(w^Tx=\log(1)=0\),因此逻辑回归的目的就是求参数\(w\)使得正样本\(w^Tx>0\)负样本\(w^Tx<0\)。
使用交叉熵损失函数,在二分类问题中
\(y^i\)是样本\(x^i\)的真实标签,\(\hat{y}^i\)是模型的预测标签,正样本的损失是\(\log(\hat{y})\)负样本的损失是\(\log(1-\hat{y})\)
我们的目标是最小化损失函数。
SGD是通过对损失函数求偏导确定梯度方向,沿着梯度方向更新参数以最小化损失函数
# 梯度下降法
for _ in range(500):
# 利用逻辑回归做预测
y0 = logistic(w,ex)
# 计算当前的交叉熵损失
ce = cross_entropy(y,y0)
# print("第{}轮,cross_entropy = {}".format(_,ce))
# 求偏导
partial = (np.sum(ex*(ey-y0),axis=0))/N
# 更新参数
w = w-alpha*partial
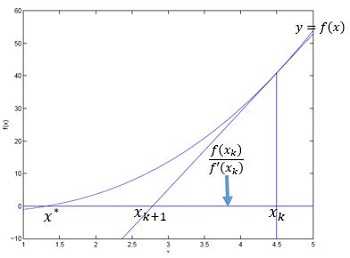
牛顿法在求解方程\(f(\theta)=0\)的根时主要是根据泰勒展开式进行迭代求解,假设有初始近似解\(x_k\),那么\(f(x)\)在点\(x_k\)处的泰勒展开式
令\(f(x)=0\)求解得到\(x_{k+1}\)
牛顿法的几何解释如下图
在逻辑回归中,损失函数的最小值在\(J‘(w)=0\)处。用牛顿迭代法求参数
标签:线性 isp 类别 迭代 最小值 sig img hat mamicode
原文地址:https://www.cnblogs.com/lepeCoder/p/logistic_regression.html