LeetCode——俄罗斯套娃信封问题

标签：序列   length   出现   就是   sub   允许   sort   array   block   

Q：给定一些标记了宽度和高度的信封，宽度和高度以整数对形式 (w, h) 出现。当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。
请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。

说明:
不允许旋转信封。

示例:
输入: envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出: 3
解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。

A：
这道题?其实是最?递增?序列（Longes Increasing Subsequence，简写为LIS）的?个变种，因为很显然，每次合法的嵌套是?的套?的，相当于找?个最?递增的?序列，其?度就是最多能嵌套的信封个数。但是难点在于，标准的 LIS 算法只能在数组中寻找最??序列，?我们的信封是由 (w, h) 这样的?维数对形式表?的，如何把 LIS 算法运?过来呢？
这道题的解法是?较巧妙的：

先对宽度 w 进?升序排序，如果遇到 w 相同的情况，则按照?度 h 降序排序。之后把所有的 h 作为?个数组，在这个数组上计算 LIS 的?度就是答案。

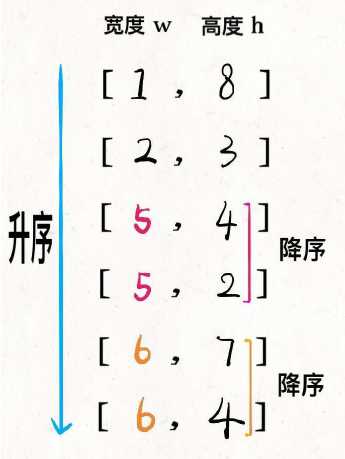
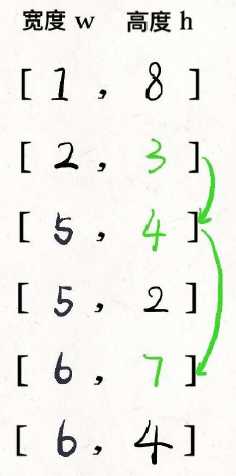
这个?序列就是最优的嵌套?案。

代码：

    public int maxEnvelopes(int[][] envelopes) {
        if (envelopes.length == 0)
            return 0;
        // 按宽度升序排列，如果宽度?样，则按?度降序排列
        Arrays.sort(envelopes, (t1, t2) -> {
            if (t1[0] < t2[0])
                return -1;
            else if (t1[0] == t2[0]) {
                if (t1[1] > t2[1])
                    return -1;
                else if (t1[1] == t2[1])
                    return 0;
            }
            return 1;
        });
        // 对?度数组寻找 LIS
        int[] dp = new int[envelopes.length];
        Arrays.fill(dp, 1);
        int max = 1;
        for (int i = 1; i < envelopes.length; i++) {
            for (int j = 0; j < i; j++) {
                if (envelopes[i][1] > envelopes[j][1])
                    dp[i] = Math.max(dp[i], dp[j] + 1);
            }
            max = Math.max(max, dp[i]);
        }
        return max;
    }

LeetCode——俄罗斯套娃信封问题

标签：序列   length   出现   就是   sub   允许   sort   array   block   

原文地址：https://www.cnblogs.com/xym4869/p/12712758.html