标签：标记   max   建立   不同的   tree   int   插入   情况   pre   

trie

介绍算法思想

trie是一种字符串处理操作,是通过将重复的地方重合起来实现对内存的压缩

比如说

对于

ILLAKIOI

ILLBEAKEDBYIOI

进行合并

那么就是通过压位处理将公共部分ILL合并起来就行了

但是我们还是有不同的部分

那么在分开存储不同的部分就行了

想到了什么?

树!!!

没错

我们将字符串通过树的形式存储

比如说字符串APL和AP APO建立trie树

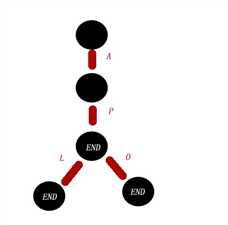
我们从根节点开始到达任意一个有end标志(字符串结尾)的节点即为一个字符串

当然没有end标记则是截取一部分

而这样的好处

1.节省空间

2.能过通过这种存储方式进行进制操作(通过一个10进制数转化为n进制数即为一个字符串,n可以为10)

算法实现

trip身为一个数据结构

也就主要为三种操作

1.插入

2.处理

处理是是情况而定的,所以这里不做说明,后面例题有讲解

插入

//仅支持a,b,c,d,e,f,g... 
void insert(string s){
	int i,len=s.size( ),u,p=0;
	for(i=0;i<len;i++){
		u=s[i]-‘a‘;
		if(!tree[p][u])tree[p][u]=++cnt;
		p=tree[p][u];
	}
	end[p]=1;
}

试着在图上模拟一下操作过程,就好懂了

例题

最大异或值

思路:先来回忆一下异或

1⊕1=0

1⊕0=1

0⊕0=0

那么我们就将输入的数转化为二进制储存进trie树

然后对输入的数进行处理

如果对于当前数位有相反的,那么ans+=1<<i

然后转移p

注意：为了最大，从最高位开始

#include<bits/stdc++.h>
using namespace std;
int tree[1000000][2],cnt;
int end[1000000];
void insert(int k){
	int i,u,p=0;
	for(i=31;i>=0;i--){
		u=k>>i&1;
		if(!tree[p][u])tree[p][u]=++cnt;
		p=tree[p][u];
	}
	end[p]=1;
}
int get(int k){
	int i,p=0,u,ans=0;
	for(i=31;i>=0;i--){
		u=k>>i&1;
		if(tree[p][!u]){
			p=tree[p][!u];
			ans+=1<<i;
		}else p=tree[p][u];
	}
	return ans;
}
int main( ){
	int ans=0;
	int i,n,k;
	cin>>n;
	while(n--){
		cin>>k;
		insert(k);
		ans=max(ans,get(k));
	}
	cout<<ans<<endl;
}

浅谈trie

标签：标记   max   建立   不同的   tree   int   插入   情况   pre   

原文地址：https://www.cnblogs.com/the-Blog-of-Mikasa/p/12715870.html