ML学习七——正则化

标签：不同   这不   数加   选择   大小   数值   哪些   特征   src   

7-1 过拟合问题

我们仍然以房价为例下面是

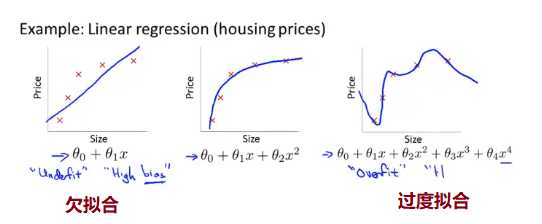
 分类问题中也存在类似的问题

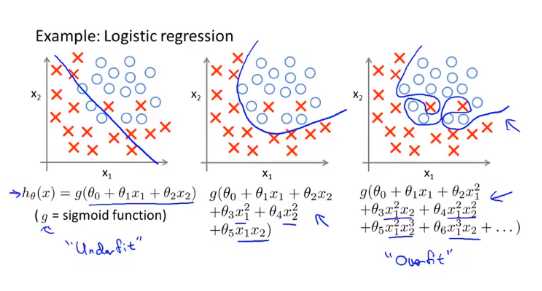
如何解决过拟合的问题？

绘制出假设模型图像再选择合适的多项式阶次，但是绘制假设模型曲线可以作为多项式阶次的一种方法，但这种并不是总是有用的，

在我们解决学习问题的过程中，我们遇到的许多的变量，并且这不仅仅是选择多项式阶次的问题，如果我们的变量很多数据训练数据非常少，就会出现过度拟合的问题

一般的我们有两个解决的办法

1. 尽量减少选取变量的数量，具体上我们可以人工检查变量清单，并以此决定哪个变量更为重要，哪些特征变量应该保留，哪些应该舍弃，也可以模型选择算法，这种算法可以自动选择，哪些特征变量应该保留，哪些应该舍弃

2. 正则化：我们将保留所有的特征变量，但是减少量级或者参数 θ_j 的大小

7-2 代价函数

正则化是怎样的运行的？

首先写出相应的代价函数，希望你可以在下面多做一些练习，现在有一些直观的例子，我们还是之前的例子

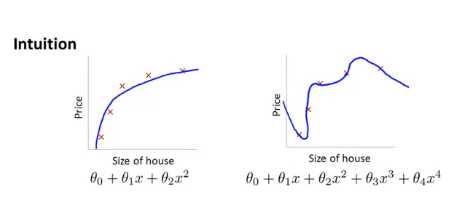
 我们不妨在函数中假如惩罚项，使得 θ₃ θ₄ 都非常小，这就意味着下面的是我们的优化目标或者说是优化问题，我们要最小化其均方误差代价函数

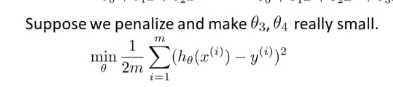
现在我们对上图的函数进行 一些修改，如图所示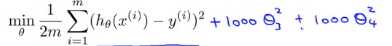，这里的1000 只是随便比较大的数，这个函数的目的是想要得到的 θ₃ θ₄ 都趋于0，就像我们去掉了过拟合化中的 θ₃ θ_4，那么过拟合中的函数就相当于二次函数，最后拟合我们的数据，实际上是一个二次函数加上了一些非常小的项，如下图所示

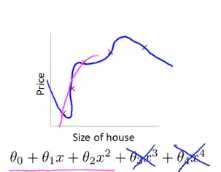
在这个特定的例子中，我们看到了加入惩罚，增大两个参数所带来的效果，总的来说，这就是正则化背后的思想

这种思想就是，如果我们的参数值较小，意味着一个更简单的假设模型，一般来说这些参数数值越小，我们得到的函数就会越平滑也就越简单，也就是说不容易出现过拟合的情景

现在让我们看一个具体的例子

我们要做的就是对代价函数（线性回归的代价函数）来缩小所有的参数，因为我们不知道该选那些参数来缩小，于是我们将修改代价函数在后面添加一个新的项

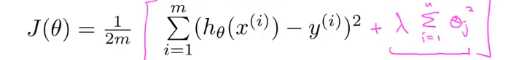如图所示，当我在式子后面加一个额外的正则化项，来缩小每个参数的值（这就是加这个项的作用），如图所示我们并没有对θ₀ 进行缩小，这是一种约定俗成的，实际上你是否加上θ₀ 对结果的影响都不大

写下正则化的代价函数

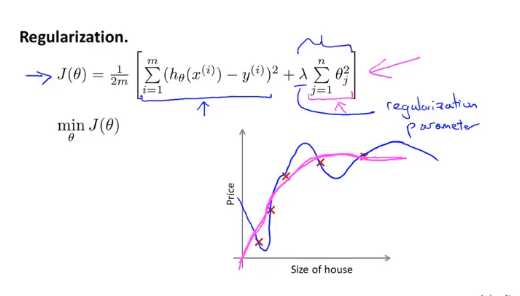
 他可以应用到逻辑回归和线性回归中

 7-3 线性回归正则化

对于线性回归我们以前推导了两种算法，一种基于梯度下降另一种基于正规方程，这一节我们将这两种算法推广到正则化线性回归中去

 最后可以整合成：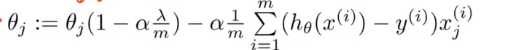

 这个数比一略小：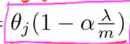

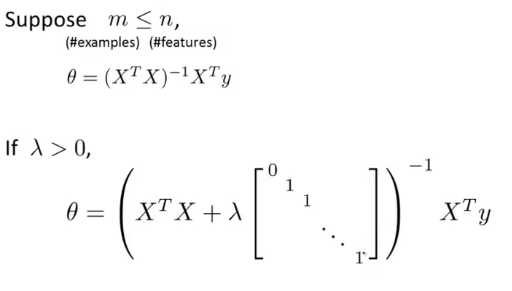
 7-4 逻辑回归的正则化

这节课我们会改进我们之前学过的两种逻辑回归的算法

以下是逻辑回归的代价函数

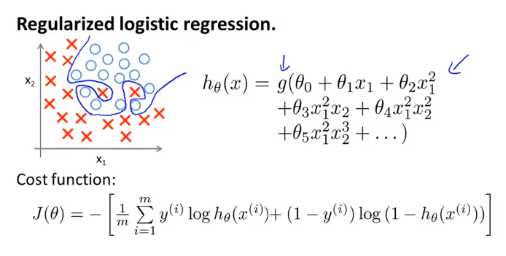
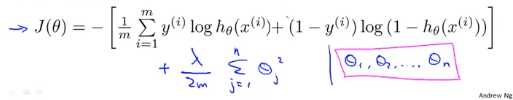
这个和之前的可能很像，但是他们的假设函数不同

 未完待续。。。。。。

ML学习七——正则化

标签：不同   这不   数加   选择   大小   数值   哪些   特征   src   

原文地址：https://www.cnblogs.com/lmr7/p/12722336.html