标签:频率 网络 贝叶斯分类 建立 如何 模型训练 先验分布 不能 排序
一.背景
1.概率:在多元下,(1)联合概率:两个事件同时发生的概率P(A,B) ,(2)条件概率:在某一事件A条件下,另一事件B发生的概率P(B|A),(3)边缘概率:某一事件发生的概率P(A);
2.独立事件:两个没有任何关系的事件互为独立事件,此时两个事件的联合概率为两者概率相乘P(A,B)=P(A)P(B),条件概率P(B|A)为事件本身的边际概率P(B)
3.先验概率和后验概率:两者都是两个事件的条件概率,但是这两个事件有关系,假设事件A‘导致‘事件‘B’,则(1)先验概率:是指根据以往经验和分析得到的概率P(B|A)---前一个条件下后一个的概率(2)后验概率:依据得到"结果"信息所计算出的最有可能是那种事件发生 P(A|B)--后一个条件下,前一个的概率
4.贝叶斯定理(后验公式):事件A和B互相有影响,A导致B,P(A|B)表示A的后验概率,P(B|A)表示B的先验概率
![]()
5.条件概率:若已知一个事件A,则我们可以得到它的边际概率,若另有一个事件B可能对其产生影响,则在B的条件下,A的概率会变化,这是因为B这个信息对事件A产生了影响,而概率可以作为量化标准。
二.贝叶斯分类器
1.贝叶斯分类器是对于分类问题而言的,在已有数据的条件下,根据贝叶斯公式,计算未知样本属于各个类别的概率,取其中最大的作为预测结果
2.目标:最小化总体风险。若有一个分类器,对于一个样本X,它可能有{c1..cn}个类别,但真实类别只有一个cj,假设λij是分类器把样本X将cj分类为ci的损失,乘以后验概率表示样本分类错为ci的期望损失,即样本对于ci的条件风险如下:
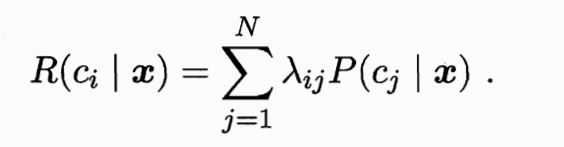
我们的目标是对于每一个样本,对于每个类别,都有风险,选择条件风险最小的那个类别作为模型最终的决策结果。
3.贝叶斯分类器:已知我们有一些种类--A--c,要知道能产生什么样的数据--B--x。贝叶斯公式可得:公式左边为后验概率,是我们建模的目的-----给定一个样本,预测它各个类别的概率;公式右边P(X)表示给定的样本所占样本空间的比例,它与类别无关;公式右边分子表示样本和类别的联合概率;P(c)是类的先验概率,表示样本空间中各类样本所占整体类别的比例;P(X|c):在类别c下,X出现的概率,一般是根据生活常识所作的模型假设,比如服从某种分布。
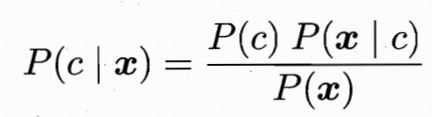
4.模型估计:根据上式进行估计预测样本各个类别的概率,选择其中概率最大的作为模型的预测值,其中P(x)可以观测得到,而P(c)和P(x|c)需要进行估计,当训练集包含充足的独立同分布的样本时,P(c)可通过频率估计得出;对于P(x|c),它也被称为似然,用频率来进行估计是不合适的,因为有一些样本取值在训练集中没有出现,‘未被观测到’和‘观测为0’是不同的。
5.模型训练:我们需要估计P(X|c)的值,而P(X|c)涉及到所有属性的联合概率,所以提出一种策略:先假设其具有某种确定的概率分布的形式,再基于已有的数据集,对概率分布的参数进行估计,如下公式利用数据集对参数进行估计--参数对于数据集的似然:
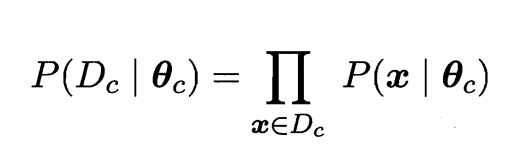
连乘易造成下溢,所以使用对数似然:
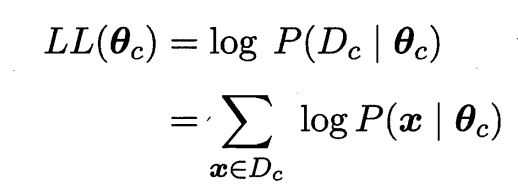
又因为我们的目标是使得样本属于某个类别的概率要尽量大(保证模型精度),所以我们要最大化似然(MLE),即找到使得似然最大的参数:
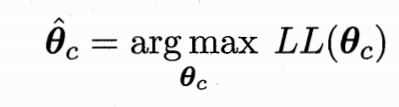
缺陷:估计结果的准确性依赖于所作的概率分布假设,它不一定符合真实数据分布。所以需要经验进行合理假设
三.朴素贝叶斯分类器
1.属性条件独立性假设:对已知类别,假设所有属性相互独立,则有
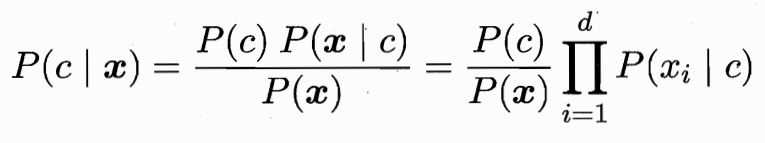
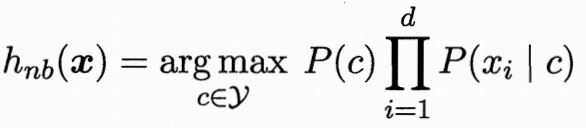
2.拉普拉斯修正--N为训练集中可能的类别数--避免了因训练样本集不充分导致的概率估计值为0的问题,当训练集变大,估计值趋于实际值:
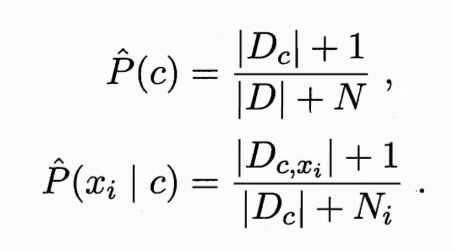
3.优缺点:模型假设不容易满足,能够处理高维数据,特别是稀疏的高维数据,它是一类模型
伯努利模型:(虚拟变量)定性变量--文本
高斯模型:(连续)定量变量---
多项式模型:都可以,--文本
四.半朴素贝叶斯分类器
1.放松‘属性条件独立性假设’:适当考虑一部分属性间的相互关系,既不需完全计算联合概率,又不会忽略比较强的属性关系
五.补充
1.判别式模型和生成式模型
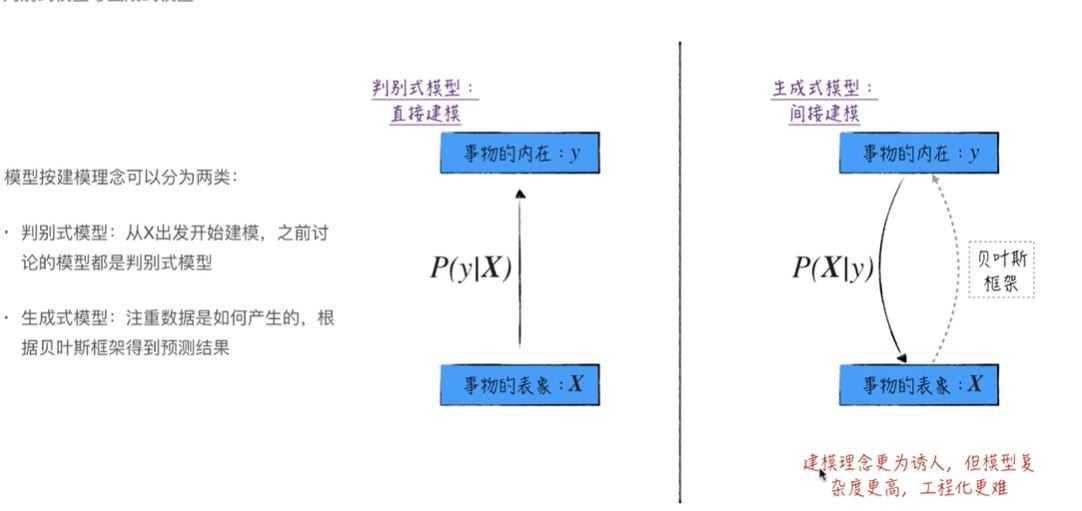
(1)判别式模型:已知样本和标签,观测数据X的大概规律来建立可能正确的模型框架,通过数据训练得出最终模型,最终进行预测y。关键点在于根据数据建模P(y|x),知道样本x后要能预测出类别y。比如决策树、神经网络,SVM等
(2)生成式模型:已知样本和标签,观测类别对数据的影响(什么样的类别y可能对于什么样的样本x),对样本和类别的联合概率(x,y)分布建模,由此获得后验概率P(x|y)。关键点在于要注重数据是如何产生的,知道样本x后要能预测出类别y,还要可以够通过y来生成样本x。比如知道模型能生成数据:创作小说等。
2.监督式和非监督式
(1)监督式:训练数据时,每个样本的P(y)是可以观测的,P(X|y)也是可以观测得到的。
(2)非监督:y不可观测,但是我们可以通过算法估计得到,因为生成式模型在于理解数据,不给y也能理解数据,给了就更加方便。
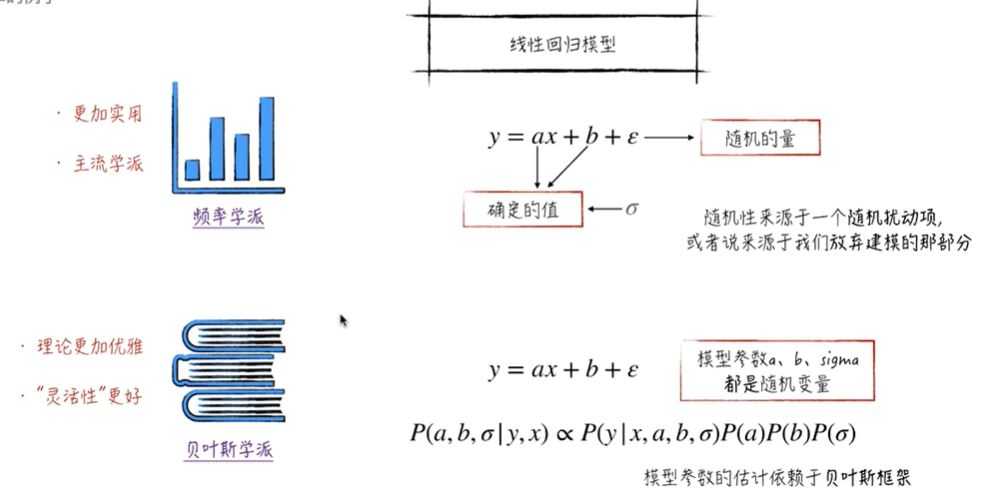
3.频率学派和贝叶斯学派:模型的随机性来自哪?
(1)频率学派:认为模型参数虽然是未知的,但是是一个客观存在的确定值,误差项是随机变量,但误差项服从某个正太分布,这也是确定的。所以随机性来自于我们无法观测的或模型无法捕捉的那部分。
(2)贝叶斯学派:任务模型参数和误差项都是不能观测到的随机变量,其本身也有分布,我们先假定这些参数服从一个先验分布,然后基于观测到的数据(X,y)计算它的后验分布。
4.期望最大化算法(Expectation-Maximization,EM)和极大似然估计方法(Maximum Likelihood Estimate,MLE)
5.文本分类:对一些文本数据进行分类
(1)数据清洗:对文本进行处理,文本指很多文字的组合,文字通常指语义单元,更接近于词
【1】无用词清洗,比如停用词/语气词等(的、了、啊、噢...)
【2】中文分词:用算法或模型把一段文本切成一个个文字(词)
(2)文本数字化:把文字转为数字,
【1】字典转换法:把所有的文字进行排序,形成一个n维的字典,字典里的每一个文字对应一个变量di,用一个n维的向量来表示文本:当文字出现在文本里,则相应的变量等于1,否则为0,漏掉很多信息---比如文字序列的信息
(3)文本的特征提取:
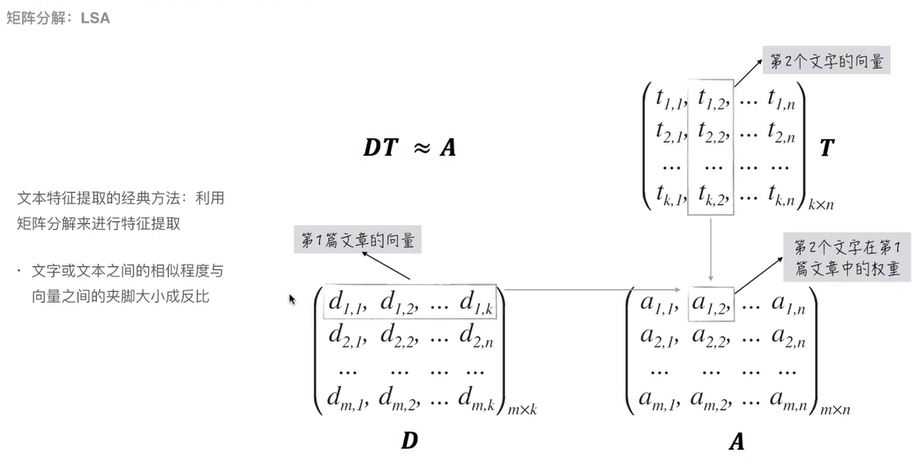
【1】矩阵分解LSA:文本表示矩阵*文字的表示向量
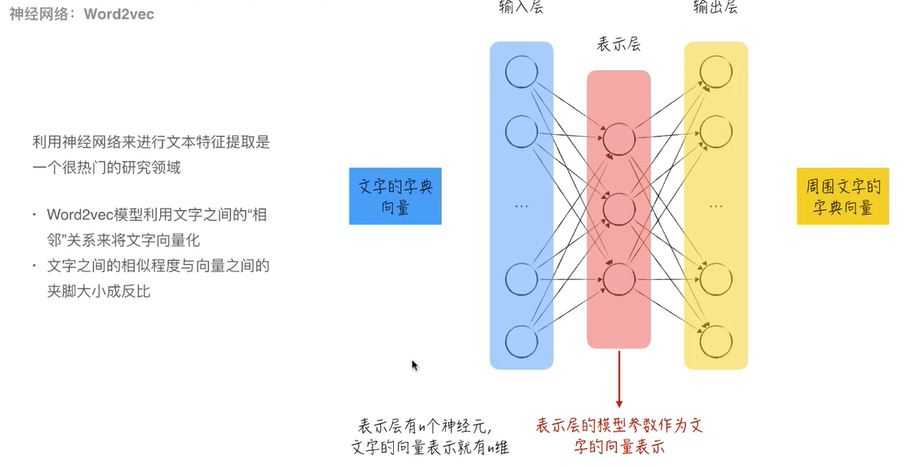
【2】神经网络:word2ves:输入文字的字典向量,输出周围文字的字典向量
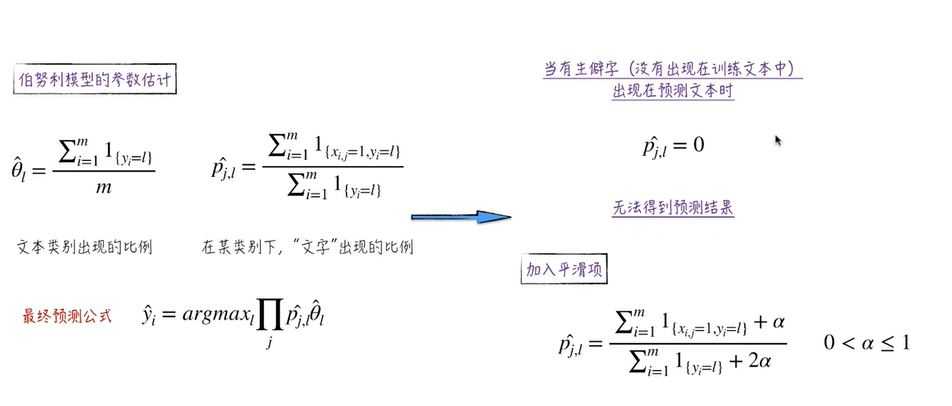
(4)伯努利模型:文本主题只与文字的出现是否有关,仅仅考虑词组是否出现,而没有考虑出现的多少
【1】xi只有两种取值1或0,与字典序特征提取一样
【2】字出现的概率随着类别的不同而不同,对于不同的类别来说,同一个字出现的概率不一样,比如‘我’在正例出现概率为0.5,在反面出现概率为0.3,两者无关
【3】文本类别的分类,分类问题所有类别的概率之和为1
【4】下面Li表示第i个文本(包括类别)出现的概率,我们要让所有文本出现的概率最大,用似然估计参数

【5】生僻字:没有出现在训练文本中,却出现在预测文本中的文字----加入平滑项
(5)多项式模型:文字出现的次数与文本分类有关,词组的出现次数是零次或多次,而不是出现与否


(6)TF-IDF:(term frequency–inverse document frequency):
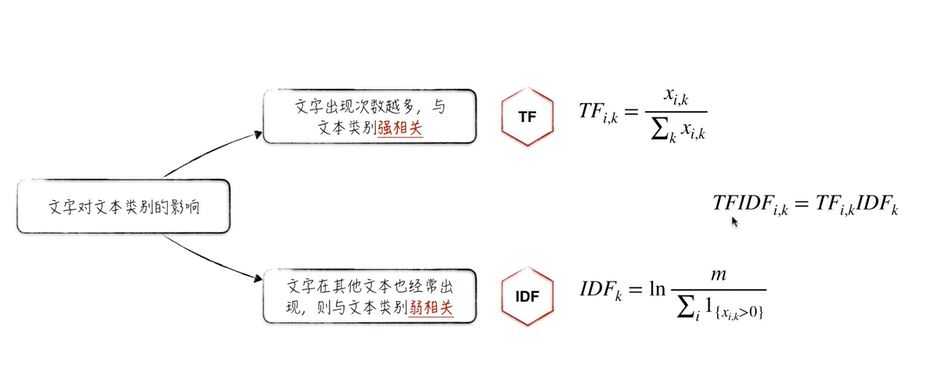
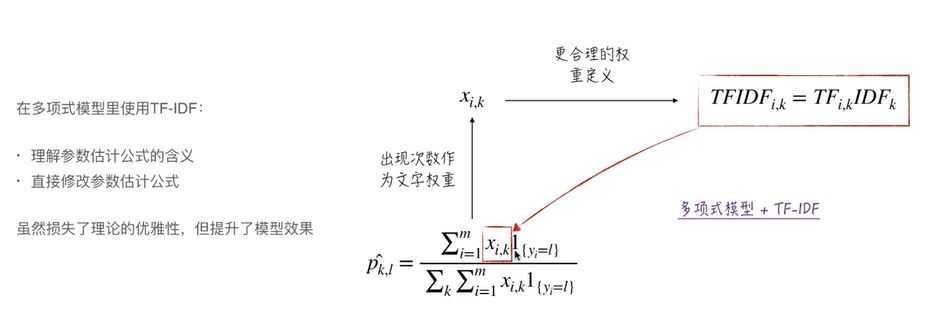
6.TF-IDF:
标签:频率 网络 贝叶斯分类 建立 如何 模型训练 先验分布 不能 排序
原文地址:https://www.cnblogs.com/yu-liang/p/12702594.html