标签:gdb time rom 学习过程 重要 roman 就是 位置 个数
[1] 树是由节点和边组成,有且仅有一个节点成为根节点;
[2] 树中有若干个不相交的子树,每个子树本身也是一棵树;
[3] 除根节点以外,树中每个节点只有一个父节点,但可以有多个子节点;
[4] 空集合也是树,即为空树,空树中没有结点;
[1] 结点的度:一个结点含有的子结点的个数; eg:结点2的度为2
[2] 树的度:一棵树中,最大的结点的度; eg:树的度为2
[3] 根结点:所有节点的祖先,没有父亲的结点; eg:结点1
[4] 父结点:含有子结点的结点; eg:结点2是结点4,5的父节点
[5] 子结点:度为0的结点; eg:结点4,5是结点2的子节点
[6] 子孙结点:以某结点为根的子树中任一结点; eg:结点2,3 … 10是结点1的子孙结点
[7] 堂兄弟结点:双亲在同一层的结点; eg:结点4和6互为堂兄弟结点;
[8] 叶子结点:(终端结点)度为0的结点; eg:结点8,9,10为叶子结点;
[9] 深度:树中结点的最大层次; eg:该树的深度为4;

图1. 树的组成
[1] 一般树:任意一个节点的子节点的个数都不受限制;
[2] 二叉树:
一般二叉树:每个节点最多含有两个子树;
满二叉树:除了叶子结点之外的每个结点都有两个孩子结点,每一层都被完全填充;
完全二叉树:除了最后一层之外的其他每一层都被完全填充,并且所有结点都保持向左看齐;(见图1)
[3] 森林:由m棵互不相交的树的集合(m>=0);
[1] 二叉树的存储:
顺序存储——数组
优点:查找某个节点的父节点和子节点(也包括有没有子节点)速度很快;
缺点:耗用内存空间过大;
存储结构:typedef ElemType BTree[MaxSize];
举例说明:
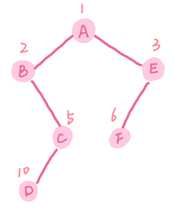
图2. 二叉树

链式存储——链表
优点:耗用内存空间小
缺点:查找父节点不方便
节点结构:typedef struct node{
ElemType data;
struct node lchild,rchild;
}
[2] 一般树的存储
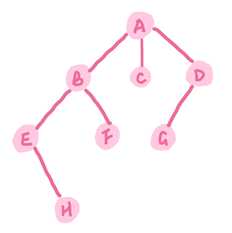
图3. 一般树
① 双亲表示法:取一块连续的内存空间,在存储每个结点的同时,各自都附加一个记录其父结点位置的变量。——求父结点方便,不方便求子结点;
数组存储:

② 孩子表示法:将树中的每个结点的孩子结点排列成一个线性表,用链表存储起来。对于含有 n 个结点的树来说,就会有 n 个单链表,将 n 个单链表的头指针存储在一个线性表中——适合找孩子结点;
链表存储:

图4. 孩子表示法
③ 双亲孩子表示法:结合双亲表示法和孩子表示法。
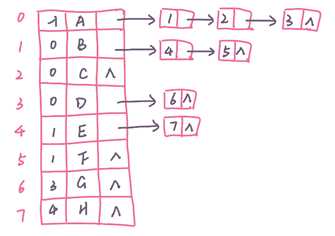
图5. 双亲孩子表示法
④ 二叉树表示法:由孩子指针域、数据域和兄弟指针域组成,其中孩子指针域,表示指向当前结点的第一个孩子结点,兄弟结点表示指向当前结点的下一个兄弟结点。
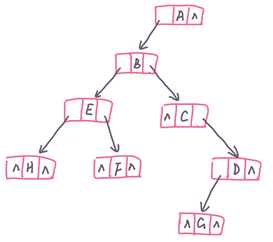
图6. 二叉树表示法
[3] 森林的存储
二叉树表示法:
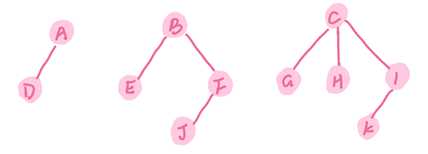
图7. 初始森林
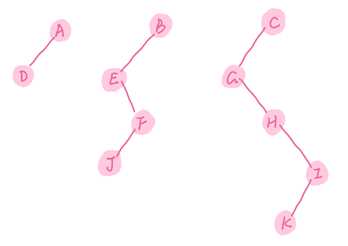
图8. 将森林中的每棵子树变为二叉树
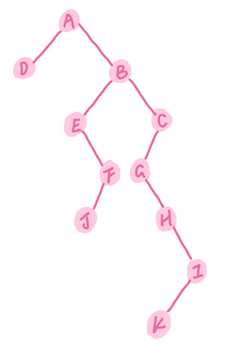
图9. 合并每一棵二叉树
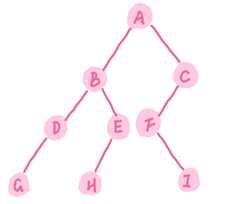
图10. 二叉树
[1] 先序遍历: (根左右) ABDGEHCFI
[2] 中序遍历: (左根右) GDBHEAFIC
[3] 后序遍历: (左右根) GDHEBIFCA
[4] 已知两种遍历序列求原始二叉树:
(1)先序,中序和后序三种遍历中,只知道其中任意一个是无法还原原始的树结构。
(2)通过先序和中序 或者 中序和后序 两种方式可以还原原始的二叉树。但是通过先序和后序是无法还原的。
[1] 树是数据库中数据组织的一种重要形式
[2] 操作系统父子进程的关系本身就是一棵树
[3] 面向对象语言中类的继承关系本身就是一棵树
[4] 赫夫曼树
备注:学习过程中难免会出现很多错误,请大家指教!有问题可以直接评论我,谢谢!
标签:gdb time rom 学习过程 重要 roman 就是 位置 个数
原文地址:https://www.cnblogs.com/ZHOUsya/p/12728318.html