标签：etc fir absolute specific xor res float efi find
题意：给出一棵树，要求给树上的每条边赋权值，使得任意两个叶子节点的路径上所有权值异或之后为0，边数n范围为[3,1e5]，求使用的不同权值数的最小值和最大值。
题解：
任取一个叶子节点为树根建树。则题意可转化为
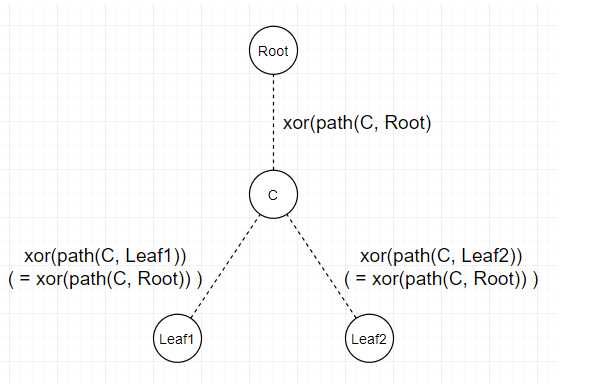
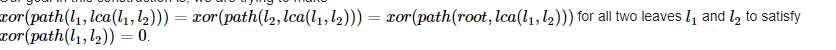
首先考虑最小值
由异或的性质（a^b^b=a,总存在c使得对任意a,b有a^b^c=0）知：
当链长为2n+1的时候，我们总可以用唯一的数构造出一条路径使其与lca到根的值相等（设这个值为x，只需填充这条链的值全为x）
当链长为2n的时候
-如果lca到根的异或值为0，都填充1即可让这条链异或值为0
-否则：填充m组（1,2,3）,n组（1，1），使3m+2n+1=（链长），最后一个位置填充lca到根的值，不难看出这个值同样不大于3（因为依照前面的构造过程，不存在大于3的边，则异或结果也不大于3）
You have unweighted tree of n vertices. You have to assign a positive weight to each edge so that the following condition would hold:
Note that you can put very large positive integers (like 10(1010)).
It‘s guaranteed that such assignment always exists under given constraints. Now let‘s define f as the number of distinct weights in assignment.
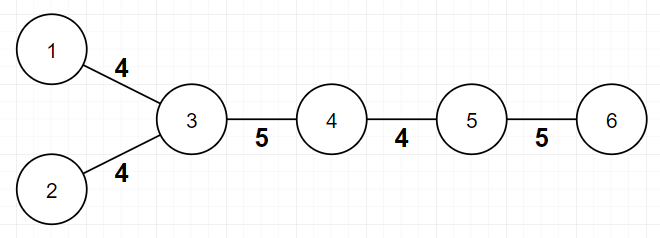In this example, assignment is valid, because bitwise XOR of all edge weights between every pair of leaves is 0. f value is 2 here, because there are 2 distinct edge weights(4 and 5).
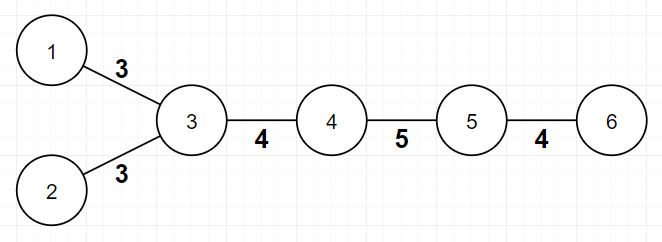In this example, assignment is invalid, because bitwise XOR of all edge weights between vertex 1 and vertex 6 (3,4,5,4) is not 0.
What are the minimum and the maximum possible values of f for the given tree? Find and print both.
The first line contains integer n (3≤n≤105) — the number of vertices in given tree.
The i-th of the next n−1 lines contains two integers ai and bi (1≤ai<bi≤n) — it means there is an edge between ai and bi. It is guaranteed that given graph forms tree of n vertices.
Print two integers — the minimum and maximum possible value of f can be made from valid assignment of given tree. Note that it‘s always possible to make an assignment under given constraints.
1338B - Edge Weight Assignment
标签：etc fir absolute specific xor res float efi find
原文地址：https://www.cnblogs.com/curezero233/p/12730242.html
