独立性检验

标签：相关   使用   class   有关   使用说明   假设   精确   产品   范围   

前言

数学原理

\(H_0：\)先假设两个变量\(A\)，\(B\)是无相关关系的，\(\chi^2\)的观测值\(k_0\)越大，则与之对应的假设事件\(H_0\)成立的概率越小，那么\(H_0\)不成立的概率越大，即两个变量相关的概率越大。

使用说明

独立性检验中的表格的解读：

• 使用实例：比如计算得到\(\chi^2=8\)，则有\(8>7.897\)，而7.897对应概率值为0.005，故有\(1-0.005=99.5\%\)以上的把握认为“两个变量有关”，但还是有低于\(0.5\%\)的判断出错可能性，并不是百分之百。

典例剖析

例1【2017全国卷2文科19题理科18题高考真题】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg）, 其频率分布直方图如下：

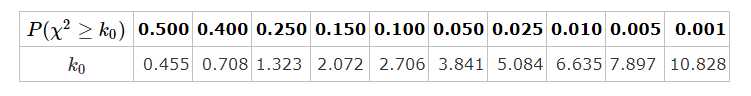
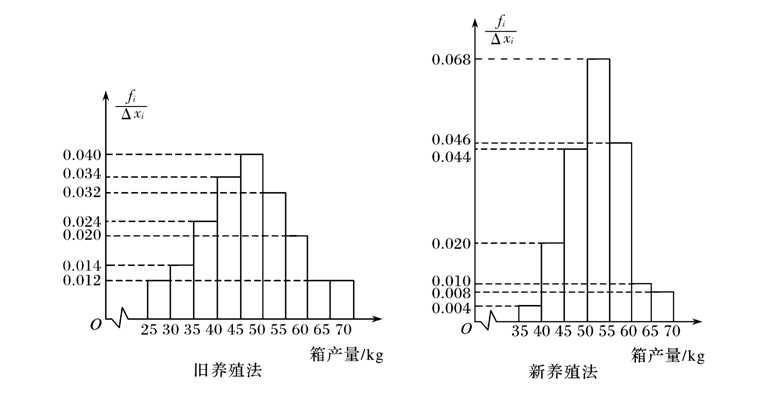
（1）记\(A\)表示事件“旧养殖法的箱产量低于50kg”，估计\(A\)的概率；

分析：本题实质是考查用频率估计概率，所以要会根据频率分布直方图计算频率。

由于“旧养殖法的箱产量低于50kg”的频率为\((0.012+0.014+0.024+0.034+0.040)\times 5=0.62\)，

故所求概率\(P(A)=0.62\)。

同理得到“新养殖法的箱产量低于50kg”的频率为\((0.004+0.020+0.044)\times 5=0.34\)

（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关，参考数据表格如下：
\(\begin{array}{c|lcr} P(\chi^2\ge k_0) & 0.050 &0.010 &0.001 \\hline k_0 & 3.841 & 6.635 & 10.828 \end{array}\)

分析：由上问可知，“旧养殖法的箱产量低于50kg”的频数为\(100\times 0.62=62\)，

则“旧养殖法的箱产量不低于\(50kg\)”的频数为\(100-62=38\)，

“新养殖法的箱产量低于\(50kg\)”的频数为\(100\times 0.34=34\)，

则“新养殖法的箱产量不低于\(50kg\)”的频数为\(100-34=66\)，由此得到二列联表如下：

由上表计算得到\(\chi^2=\cfrac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}\)

\(=\cfrac{200(62\times 66-38\times 34)^2}{(62+38)(34+66)(62+34)(38+66)}=15.705>6.635\)

故有99%以上的把握认为，二者有关联。

（3）根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较。

分析：本题目的难点有：到底从哪些角度进行比较？每一个角度下的数值的计算方法。

数据的极差：旧，\(25-70\)；新，\(35-70\)，极差反映了数据的取值范围和数据的几种程度，当然误差是有的；

数据的众数：旧，\(47.5\)；新，\(52.5\)，众数反映了出现次数最多，

数据的平均数：旧，\(47.1\)；新，\(52.35\)，平均数反映了一组数据的平均水平，

数据的方差(标准差)：比较精确的反映了数据的分散和集中程度，将这种程度数量化了。

本题目从运算量和问题出发，可以从数据的范围和数据的中位数(或均值)两个角度作答。

“旧养殖法”的数据分布在\(25-70\)之间，“新养殖法”的数据分布在\(35-70\)之间，

故从数据范围来看，新养殖法的数据更集中，优于旧养殖法；

“旧养殖法”的平均数(中位数)分布在\(40-45\)之间，“新养殖法”的平均数(中位数)分布在\(50-55\)之间，

从平均数(中位数)角度来看，新养殖法也优于旧养殖法。

独立性检验

标签：相关   使用   class   有关   使用说明   假设   精确   产品   范围   

原文地址：https://www.cnblogs.com/wanghai0666/p/12730860.html