然后通过你敏锐的观察力,发现他们有些许的规律
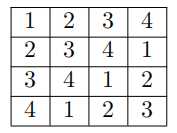
若$k=n$,$a[i][j]=(i+j-2)%n+1$
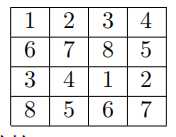
若$k=2*n$,奇数行:$a[i][j]=(i+j-2)%n+1$;偶数行:$a[i][j]=(i+j-2)%n+n+1$
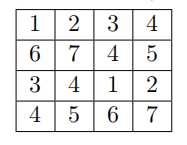
若$n<k \leq 2n$:在$k=2n$的基础上把大于$k$的换成$x-n$即可。
接下来就是怎么找到一个$n$使得$n \leq k \leq 2n$。令$n=2*\left \lceil \frac{k}{4} \right \rceil $即可。特判$k=1$
$Robot Arms$:$n+1$个节点,$n$条长度为$d[i]$的边,第$i$步可以向上下左右任意方向走$d[i]$步,要求从$(0,0)$出发走n次最终能到达$(x_i,y_i)$,输出方案。
题解:题目好绕啊。加入已有一个$d$序列,每次运动,坐标加减的值是一样的,最终能到达的地方的$x+y$奇偶性是相同的,所以$m$个目标节点的$x_i+y_i$必须是一样的,否则不合法。关于$d$序列的构建,考虑优秀的二进制。令$d[k]=2^{40-k}$ $k \leq 40$。发现这样能到达的地方横纵坐标和一定是奇数(除$1$外全部都是偶数),如果$x_i+y_i$为偶数的话,在d的最后再加一个$1$就好。这样的话,每一步能到达的范围会形成一个菱形(画个坐标轴理解理解),保证左右地方都能被经过。对于输出走的方式,反过来从$(x_i,y_i)$走到$(0,0)$,这个过程考虑贪心。每次选择$x,y$中较大的那个,向靠近$(0,0)$那个方向走一步,注意输出的是反着的。
$Not Same$:大小为 $n $的集合 $a1, a2, . . . , an$,满足 $1 ≤ ai ≤ n$。每次你可以选择一个子集的元素并且把这个子集的元素都$1$,你需要在至多 $n + 1 $次操作之内把所有数变成 $0$。每次选择的子集不能相同。$1 ≤ n ≤ 1000$
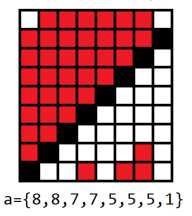
题解:列一个$n+1$行,$n$列的$0/1$矩阵,第$i$行第$j$列为$1$代表第$i$次的集合里有$j$。把$a$数组降序排列,然后以对角线为分界线往上填$a[i]$个$1$,如果格子不够,再回来从最下边一行接着填。这样一定不会有集合是相同的。证明感性理解。偷张图好理解
$Inverse of Rows and Columns$:给定一个 $n × m$ 的 $01$ 矩阵,你可以选择任意行翻转任意列翻转($0$变$1$,$1$变$0$)。求最后能否将整个矩阵变成有序的。有序即$a_{1,1} \leq a_{1,2} ...\leq a_{2,1}...\leq a_{n,m}$
题解:首先特判$n=1$。为满足题目的条件,最终的矩阵一定满足两个条件中的一个:$A.$第一行全是$0$;$B.$最后一行全是$1$。两种情况分别来一遍,那个符合那个就是答案,都不符合就无解。以$A$为例,若$a[1][i]=1$,则翻转第$i$列。翻转完后若存在答案,有两种情况:$1.$所有行都只有$0$或只有$1$,那么就全翻成一样的就好;$2.$有且仅有第$k$行同时包含$0$或$1$,且$0$全部在左边,$1$全部在右边,或者反过来,只需要把第$k$行翻成前$0$后$1,2~k-1$行翻成$0$,$k+1~n$翻成$1$。$B$是类似的。