机器学习知识复习

标签：更新   休息   art   误差   奖惩   预测   nbsp   比较   就会   

什么是机器学习？

定义是从数据中寻找关系f(x)，在新数据中根据f(x)做出预测。我认为机器学习根基就是大数定律，在一部分数据寻找得规律可以一定程度反映出全局数据得特性。

那怎样去寻找这种关系呢？

机器学习的分类

一、有监督学习

有监督学习就是训练数据对应的有label，在训练过程中根据label来判断划分是否正确

二、无监督学习

训练数据中无label，根据数据的分布特征来划分

三、半监督学习

由于大数据的到来，数据量太多，所以在训练数据中可以用只包含部分label的数据来训练

四、强化学习

根据每次的结果进行奖惩来优化

回归分析

回归分析就是根据数据拟合出一条曲线，该曲线能大致反映数据得规律，有一元回归，多元回归

下面介绍一下一元回归----线性回归

线性回归

线性回归是我们根据数据拟合出一条直线，该直线能大致反映出数据的规律，我们衡量反映数据规律程度的度量(loss)就是均方误差，即拟合出的直线预测值与真实值的差距

线性回归中我们怎样去更新拟合的曲线，使它更好的缩小loss(即预测值与真实值的差距)？

梯度下降法

向梯度的反方向以规定的步长去寻找极小点。

为什么可以用梯度下降法？

因为我们线性回归中的loss函数是一个凸函数，它存在极小值点

求梯度的方法就是使用偏导数，线性回归中更新参数的公式如下：

P_i+1  = P_i - α* ∂(f(P_i))/∂P_i

经过梯度下降法寻找出合适的曲线之后我们要对我们找到的这条曲线进行评估

模型评估方法

MSE，均方误差

R方值 ，相当与1-MSE/方差

MSE越小越好，R方值越接近1越好

那有些数据展现出来的线性相关性很差，需要曲线去拟合的时候怎么办？

多项式扩展

多项式扩展相当于把低维的特征映射组合到高维中去，其线性相关性就会增大

(x₁,x₂)----->(x₁,x₂,x₁²,x₂²,x₁x₂)

即y=a*x1+b*x2映射成y=ax1+bx2+cx₁²+dx₂²+ex₁x₂

可以将上述(x₁,x₂,x₁²,x₂²,x₁x₂)替换成z1,z2,z3,z4,z5，其形式就会变成线性，其中原理是泰勒定理

z1,z2,z3,z4,z5相当于x1,x2组合出来的新特征，而这些特征在数学推导上有泰勒定理可以认为是正确的

多项式扩展目标就是提升模型的精度，但维数特别高的时候容易过拟合，比如一个二次函数就能很好拟合的数据，你用高次函数会拐很多不必要的弯

解决方案：引入正则化

正则化

正则化其实就是一项反映模型复杂程度的项，加在loss后面，可以缓解过拟合现象。

L1正则化：各个参数的绝对值之和

L2正则化：1/2*(ω)²,它使参数权重更加接近原点

上述是回归任务，当我们遇到分类任务的时候怎么办？

在线性回归的基础上加一个sigmoid函数，便成为了Logistic回归

Logistic回归

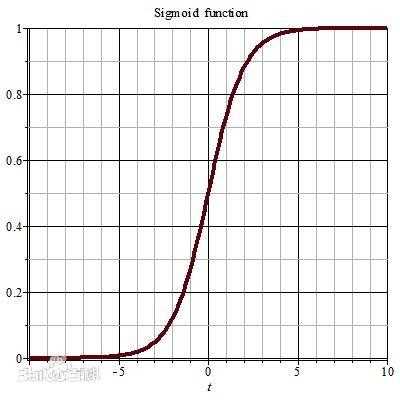
Logistic回归是一个二分类算法，在线性回归的基础上加上一个这样一个函数，当y>0.5时，为正样本；y<0.5时，为负样本，进而实现分类

二分类算法有了，那怎么实现多分类呢？

Softmax回归，Logistic的推广

Softmax是对于给定的测试输入，我们想用假设函数针对每一个类别j估算出概率值，y_hat可以取k个值，每个值相当于一个类别的概率值，最后比较哪个概率大，就认为属于哪个类别。

公式推导见:https://baike.baidu.com/item/softmax%20%E9%80%BB%E8%BE%91%E5%9B%9E%E5%BD%92

 外带一点训练时候的方法

K折交叉验证

以三折交叉验证为例，将训练集分为1，2，3，三部分

训练集：1，2   验证集：3 ----->model1

训练集：1，3   验证集：2 ----->model2

训练集：3，2   验证集：1 ----->model3

然后选择最优的结果进行输出

休息一下理一下决策树的思路

机器学习知识复习

标签：更新   休息   art   误差   奖惩   预测   nbsp   比较   就会   

原文地址：https://www.cnblogs.com/lizhe-cnblogs/p/12731221.html