标签:证明 com 等于 构造 存在 注意 使用 否则 --
1.最大匹配里的边,每一条边都需要使用顶点覆盖,也就是说最小点覆盖大于等于最大匹配数
2.我们任取一个最大匹配,将在最大匹配内的点染成蓝色,不在最大匹配内的点染成黑色
显然,不可能有边的两个端点都是黑色,也就是说每条边都至少有一个蓝色点.
我们只需选择蓝色点即可,考虑在每条匹配边中只选一个蓝点。
选择蓝点的方法如下:
如果存在一个端点与黑色点直接相连,那么我们选择这个蓝色点,否则随便选择一个点即可,这样我们就构造了一种大小为最大匹配的最小点覆盖。
注意如果存在下面的情况,则我们需要在1--2这条边中同时选择两个蓝色点来盖住黑色点。但下面这种情况是不存在的。
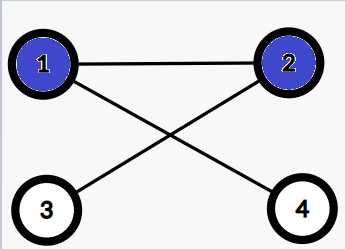
1--2是匹配边,1,2点均是蓝色
3,4都是未匹配点,1-4,2-3是未匹配边
因为如果是这样的话,就会存在增广路。
综上:最小点覆盖=最大匹配
标签:证明 com 等于 构造 存在 注意 使用 否则 --
原文地址:https://www.cnblogs.com/cutemush/p/12732407.html