Computational Geometry

标签：旋转   org   splay   方程组   abc   图片   sum   mat   png   

矩形重叠

看过某司一道笔试题：给\(n\)个矩形左下和右上坐标（不能斜放），求重叠最多处矩形个数。
这道题本身不难：可以遍历所有矩形边界组成的点，计算该点被多少矩形包围，从而选出最大值。
由此引申出一个问题：判断两个矩形重叠。

• 如果正向思考，会有很多种情况：包含、重叠某个角、交叉...
  那么如果逆向思考：什么情况两个矩形不重叠？无非就是\(A(p_1, p_2)\)在\(B(p_3, p_4)\)的上下左右：

取反后用De Morgan‘s law化简就是重叠的情况：

线段交点

联立方程组求解当然没问题，也可以用几何的方法解：

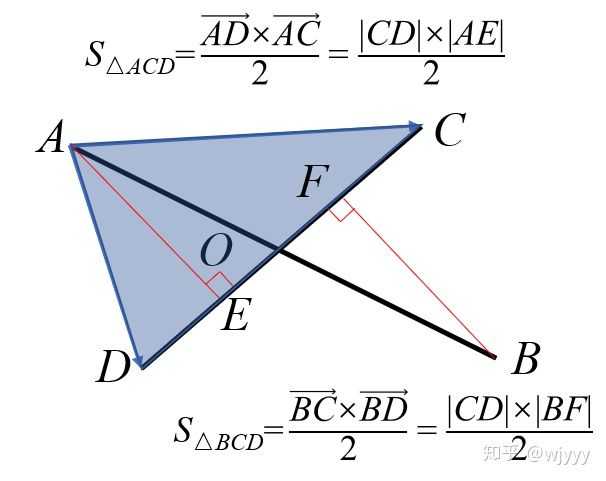
易知，\(\frac{AO}{BO}=\frac{AE}{BF}=\frac{S_{ACD}}{S_{BCD}}\)，两个三角形面积可以用叉积求得，又\(\vec{AO}=\frac{AO}{AB}\vec{AB}=\frac{AO}{AO+BO}\vec{AB}\)，所以\(\vec{O‘O}=\vec{O‘A}+\vec{AO}\)，即可求得\(O\)点坐标。

向量旋转

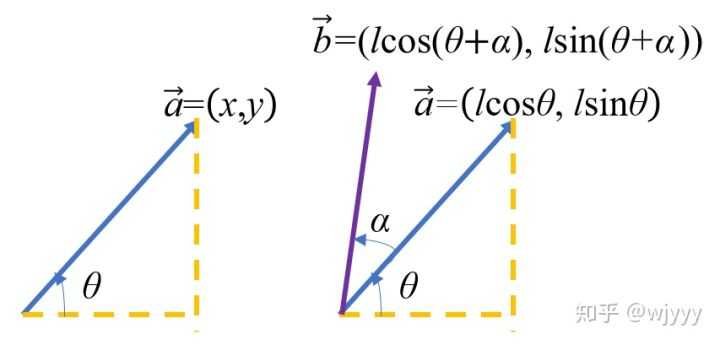
三角变换可得：

多边形面积

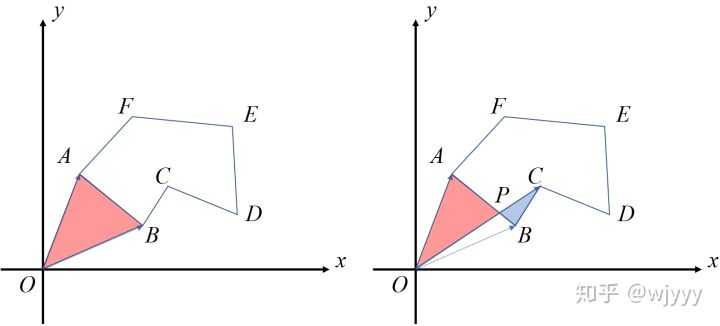
三角剖分：

即：

凸包

包围所有给定点并且周长最小的多边形。

reference
洛谷日报#142 计算几何初步

Computational Geometry

标签：旋转   org   splay   方程组   abc   图片   sum   mat   png   

原文地址：https://www.cnblogs.com/EIMadrigal/p/12371851.html