标签:inf ios void cin diff 完全 sub 一点 max
这题还是挺有意思的。
题目要求的是哈密顿路径,这个有点不好处理,我们先转化成求哈密顿回路后减去一条路径。
这就是个套路题了,我们不考虑每条路径,而考虑每一个边最多被包含在几条路径内。
对于每一个边,如果把它断开后把树分成了两个大小分别为 \(x\) 和 \(y\) 的连通块,则有 \(\min(x,y)\) 条路径通过它,也就是说从小连通块中的点出发的路径都会经过这条边一次。
放张图:
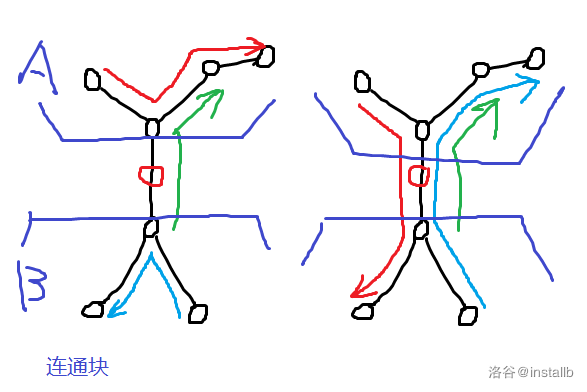
其它被覆盖的路径完全没有变化,而被圈出的路径被经过次数增加了,我们完全可以随便构造一个方案然后不停像图中这么做。
这样是答案的理论上界,而我们的方案也达到了这个理论上界。
放道类似的题。
然后把每条边的贡献加起来就好了。
下面才是重点了
接下来在于要去掉哪条路径。
如果你觉得随便去哪一条都行,就去最小的那条吧,那么连样例都过不去。
因为可能这条路径不包含在任意一个最优解中。
事实上,不经过重心的路径都不包含在任一最优解中。
因为对于树的重心,把它作根,它不存在 \(siz> \frac{n}{2}\) 的子树。可以想象如果存在 \(siz> \frac{n}{2}\) 的子树,那么必定有至少一条路径是在这棵子树内部的,因为其它的子树合起来都不够和这棵子树配对出来那么多经过这个节点的路径。
每一个子树都 \(siz\leq \frac{n}{2}\) 的子树是一定可以做到的。这很显然了,不浪费时间证明这个了。
树的重心符合这个性质,也只有树的重心符合这个性质。
这就意味着如果我们可以做到每一条路径,都是在重心的两个不同子树中各取一点相连。
就像最开始出示的那张图一样,我们要是让两条在同一个子树内的路径交叉而经过重心,则一定更优。
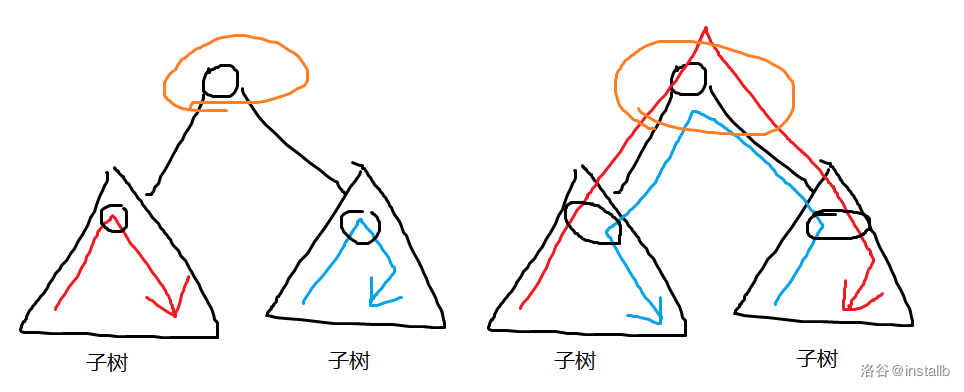
既然所有经过重心的路径都可行,那就删去最短的一条,也就是以中心为一端的边中最短的边。
如果树有两个重心,那么减去两重心之间的边。把边等效为上文的重心。
可以贴代码了
const LL INF = 0x3f3f3f3f3f3f3f3f;
LL ec = 0,hed[200005] = {0},to[400005],w[400005],nxt[400005];
void add_edge(LL f,LL t,LL cst){
++ ec; to[ec] = t; nxt[ec] = hed[f]; w[ec] = cst; hed[f] = ec;
}
LL siz[200005],mx[200005];
LL ans = 0,n;
void dfs(LL u,LL f){
siz[u] = 1;
for(LL i = hed[u];i;i = nxt[i]){
LL v = to[i];
if(v == f) continue;
dfs(v,u);
siz[u] += siz[v]; mx[u] = max(mx[u],siz[v]);
ans += 2 * min(siz[v],n - siz[v]) * w[i];
}
mx[u] = max(mx[u],n - siz[u]);
}
int main(){
ios::sync_with_stdio(false);
LL u,v,ww,g = INF,sub = INF,p1 = 0,p2 = 0;
cin >> n;
for(LL i = 1;i < n;i ++){
cin >> u >> v >> ww;
add_edge(u,v,ww);
add_edge(v,u,ww);
}
dfs(1,0);
for(LL i = 1;i <= n;i ++) g = min(g,mx[i]);
for(LL i = 1;i <= n;i ++){
if(mx[i] != g) continue;
if(!p1) p1 = i;
else p2 = i;
}
for(LL i = hed[p1];i;i = nxt[i]){
LL v = to[i];
if(p2 && v != p2) continue;
sub = min(sub,w[i]);
}
cout << ans - sub << endl;
return 0;
}
\(\sf{difficulty:\color{red}2813}\)
要求运用重心的性质以及用到一个常用的 trick,思维难度还是挺大的(想不到是重心),代码实现难度还是一如既往的小。
[AGC018D] Tree and Hamilton Path 题解
标签:inf ios void cin diff 完全 sub 一点 max
原文地址:https://www.cnblogs.com/IltzInstallBI/p/12744275.html