标签:strong data i++ 存在 算法 进制 image 最近公共祖先 最小
最近公共祖先,就是指两个节点在这棵树上深度最大的公共的祖先节点,也就是这两个点在这棵树上距离最近的公共祖先节点。
所以LCA主要是用来处理两个点之间唯一的那一条最短路径。
首先最容易想到的暴力做法:
给出节点u , v,,首先对u进行回溯一直到根节点,并对途中的节点加上标记。然后对v进行回溯,直到找到一个被标记的节点T,此时T即为u,v的LCA。
此方法写起来很简单但时间复杂度太高,故只适合查询次数极少的时候。
一般解决LCA有三种算法:
第一种,Tarjan ,离线算法,复杂度 O(V+Q) 。
第二种,倍增,在线算法,预处理复杂度 VlogV ,每次查询 O(logV)。
第三种, DFS+ST,在线算法,预处理复杂度 O(VlogV),每次查询 O(1) 。
该算法的思想为,对于任意一个结点 rt,处于 rt 的不同子树上的两个结点 u,v ,一定有 LCA(u,v)=rt 。这个结论非常显然。
首先,rt 是 u,v 的共同祖先;其次,任何深度大于 rt 的结点都只会至多存在于 rt 的一棵子树中,不可能是既是 u 的祖先又是 v 的祖先,因而 rt 是 u,v 的最近公共祖先。
此种算法需要预先知道所有的询问,并对询问进行一些预处理,即将有相同节点的询问放在一块。算法的主要思想就是在DFS过程中处理一些信息从而得到答案。
在DFS进行之前,把每个点都看作一个独立的点集且作为对应点集的代表元。
在DFS过程中每次遍历完一棵子树,回溯到当前子树的根节点 rt 时,便将这棵子树上的所有点并到这个根结点 rt 的点集里,此时根节点 rt 即为该集合的代表元。
然后对与此根节点的其他子树上的点相关的询问进行回答。设此节点为u,另一点为v,若v已经完成DFS(v是 rt 之前子树上的一个点),则 v 所在点集的代表元 rt 即为u,v的LCA。
tips:
1.点集的合并可以用并查集来完成。
2.每次询问都查询了两次,并且有且只有一次做出回答。
3.此算法必须知道预先知道所有的询问,不够灵活。
4.Tarjan 算法复杂度最低,代码也很简单,不易出错,对于可以离线的 LCA 询问, Tarjan 算法是首选。
下面关于例子讲解出自:https://www.cnblogs.com/jvxie/p/4854719.html
什么是Tarjan(离线)算法呢?顾名思义,就是在一次遍历中把所有询问一次性解决,所以其时间复杂度是O(n+q)。
Tarjan算法的优点在于相对稳定,时间复杂度也比较居中,也很容易理解。
下面详细介绍一下Tarjan算法的基本思路:
任选一个点为根节点,从根节点开始。
遍历该点u所有子节点v,并标记这些子节点v已被访问过。
若是v还有子节点,返回2,否则下一步。
合并v到u上。
寻找与当前点u有询问关系的点v。
若是v已经被访问过了,则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。
遍历的话需要用到dfs来遍历(相信来看的人都懂吧...),至于合并,最优化的方式就是利用并查集来合并两个节点。
伪代码如下:
Tarjan(u)//marge和find为并查集合并函数和查找函数 { for each(u,v) //访问所有u子节点v { Tarjan(v); //继续往下遍历 marge(u,v); //合并v到u上 标记v被访问过; } for each(u,e) //访问所有和u有询问关系的e { 如果e被访问过; u,e的最近公共祖先为find(e); } }
个人感觉这样还是有很多人不太理解,所以打算模拟一遍给大家看。
假设我们有一组数据 9个节点 8条边 联通情况如下:
1--2,1--3,2--4,2--5,3--6,5--7,5--8,7--9 即下图所示的树
设我们要查找最近公共祖先的点为9--8,4--6,7--5,5--3;
设f[]数组为并查集的父亲节点数组,初始化f[i]=i,vis[]数组为是否访问过的数组,初始为0;
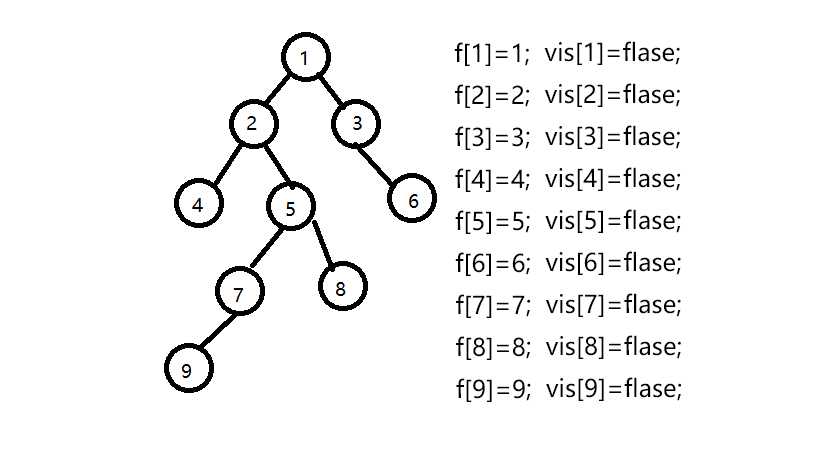
下面开始模拟过程:
取1为根节点,往下搜索发现有两个儿子2和3;
先搜2,发现2有两个儿子4和5,先搜索4,发现4没有子节点,则寻找与其有关系的点;
发现6与4有关系,但是vis[6]=0,即6还没被搜过,所以不操作;
发现没有和4有询问关系的点了,返回此前一次搜索,更新vis[4]=1;
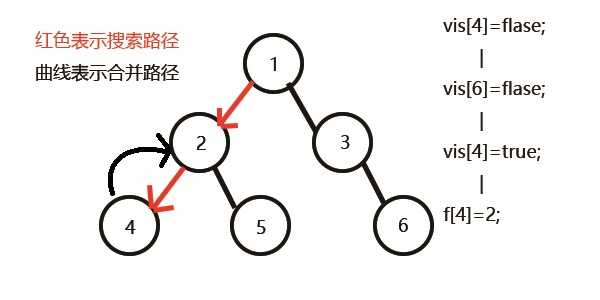
表示4已经被搜完,更新f[4]=2,继续搜5,发现5有两个儿子7和8;
先搜7,发现7有一个子节点9,搜索9,发现没有子节点,寻找与其有关系的点;
发现8和9有关系,但是vis[8]=0,即8没被搜到过,所以不操作;
发现没有和9有询问关系的点了,返回此前一次搜索,更新vis[9]=1;
表示9已经被搜完,更新f[9]=7,发现7没有没被搜过的子节点了,寻找与其有关系的点;
发现5和7有关系,但是vis[5]=0,所以不操作;
发现没有和7有关系的点了,返回此前一次搜索,更新vis[7]=1;
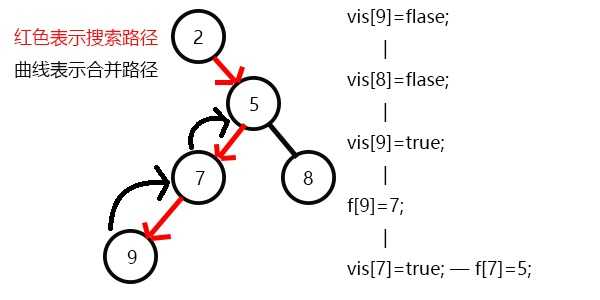
表示7已经被搜完,更新f[7]=5,继续搜8,发现8没有子节点,则寻找与其有关系的点;
发现9与8有关系,此时vis[9]=1,则他们的最近公共祖先为find(9)=5;
(find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5;)
发现没有与8有关系的点了,返回此前一次搜索,更新vis[8]=1;
表示8已经被搜完,更新f[8]=5,发现5没有没搜过的子节点了,寻找与其有关系的点;
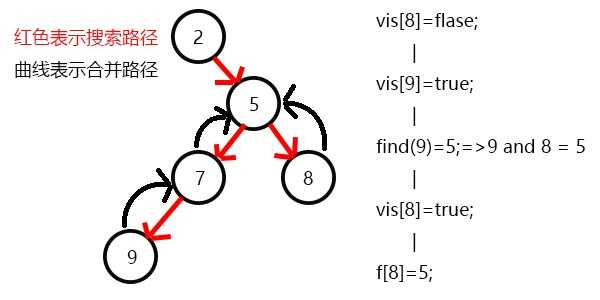
发现7和5有关系,此时vis[7]=1,所以他们的最近公共祖先为find(7)=5;
(find(7)的顺序为f[7]=5-->f[5]=5 return 5;)
又发现5和3有关系,但是vis[3]=0,所以不操作,此时5的子节点全部搜完了;
返回此前一次搜索,更新vis[5]=1,表示5已经被搜完,更新f[5]=2;
发现2没有未被搜完的子节点,寻找与其有关系的点;
又发现没有和2有关系的点,则此前一次搜索,更新vis[2]=1;
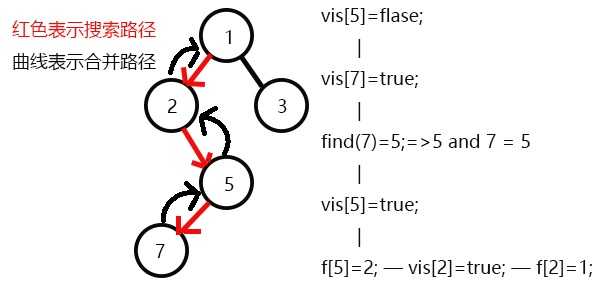
表示2已经被搜完,更新f[2]=1,继续搜3,发现3有一个子节点6;
搜索6,发现6没有子节点,则寻找与6有关系的点,发现4和6有关系;
此时vis[4]=1,所以它们的最近公共祖先为find(4)=1;
(find(4)的顺序为f[4]=2-->f[2]=2-->f[1]=1 return 1;)
发现没有与6有关系的点了,返回此前一次搜索,更新vis[6]=1,表示6已经被搜完了;
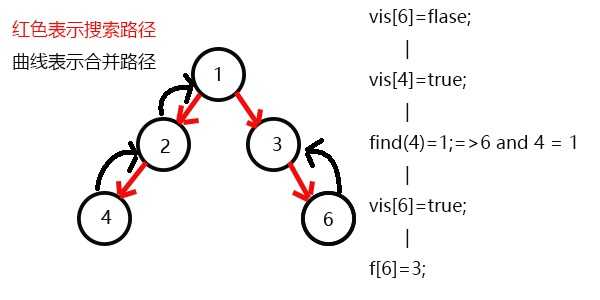
更新f[6]=3,发现3没有没被搜过的子节点了,则寻找与3有关系的点;
发现5和3有关系,此时vis[5]=1,则它们的最近公共祖先为find(5)=1;
(find(5)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1;)
发现没有和3有关系的点了,返回此前一次搜索,更新vis[3]=;
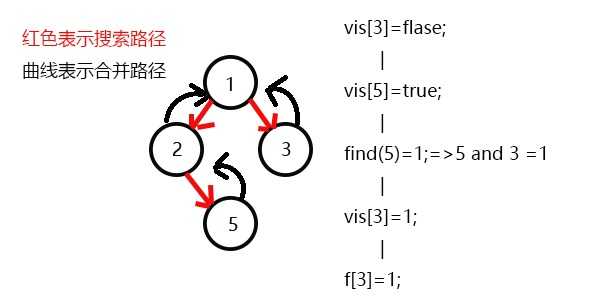
更新f[3]=1,发现1没有被搜过的子节点也没有有关系的点,此时可以退出整个dfs了。
下面讲解出自:https://www.luogu.com.cn/blog/morslin/solution-p3379
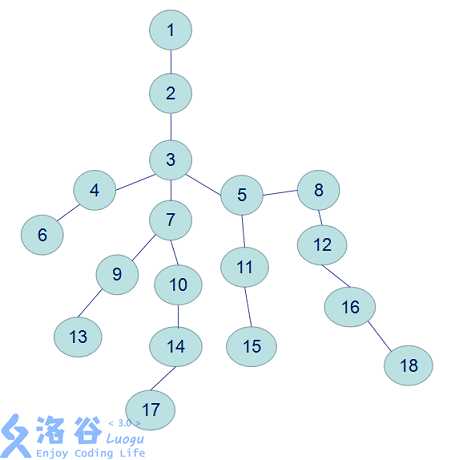
所谓倍增,就是按22的倍数来增大,也就是跳 1,2,4,8,16,32……不过在这我们不是按从小到大跳,而是从大向小跳,即按……32,16,8,4,2,1来跳,如果大的跳不过去,再把它调小。
这是因为从小开始跳,可能会出现“悔棋”的现象。拿 5 为例,从小向大跳,5≠1+2+4,所以我们还要回溯一步,然后才能得出5=1+4;而从大向小跳,直接可以得出5=4+1。
这也可以拿二进制为例,5(101),从高位向低位填很简单,如果填了这位之后比原数大了,那我就不填,这个过程是很好操作的。
以 17 和 18 为例,如果分别从 17 和 18 跳到 3 的话,它们的路径分别是(此例只演示倍增,并不是倍增LCA算法的真正路径):
17->3
18->5->3
可以看出向上跳的次数大大减小。这个算法的时间复杂度为O(nlogn),已经可以满足大部分的需求。
想要实现这个算法,首先我们要记录各个点的深度和他们2i级的的祖先,用数组deep表示每个节点的深度,fa[i][j]表示节点 i 的2j级祖先。
代码如下:
void getdeep(int u,int pre)//u表示当前节点,pre表示它的父亲节点 { deep[u]=deep[pre]+1; fa[u][0]=pre; for(int i=1;(1<<i)<=deep[u];i++) fa[u][i]=fa[fa[u][i-1]][i-1];//这个转移可以说是算法的核心之一 //意思是u的2^i祖先等于u的2^(i-1)祖先的2^(i-1)祖先,2^i=2^(i-1)+2^(i-1) for(int i=head[u];i!=-1;i=E[i].next)//注意:尽量用链式前向星来存边,速度会大大提升 { if(E[i].to==pre) continue; getdeep(E[i].to,u); } }
预处理完毕后,我们就可以去找它的LCA了,为了让它跑得快一些,我们可以加一个常数优化(来自洛谷提高组讲义)
for(int i = 1; i <= n; ++i) //预先算出log_2(i)+1的值,用的时候直接调用就可以了 lg[i] = lg[i-1] + (1 << lg[i-1] == i); //看不懂的可以手推一下
接下来就是倍增LCA了,我们先把两个点提到同一高度,再统一开始跳。
但我们在跳的时候不能直接跳到它们的LCA,因为这可能会误判,比如 4 和 8 ,在跳的时候,我们可能会认为 1 是它们的LCA,但 1 只是它们的祖先,它们的LCA其实是 3 。
所以我们要跳到它们LCA的下面一层,比如 4 和 8 ,我们就跳到 4 和 5 ,然后输出它们的父节点,这样就不会误判了。
int LCA(int u, int v) { if (deep[u]>deep[v]) swap(u,v);//保证u的深度 <= v的深度 int du=deep[u], dv=deep[v], uu=u, vv=v; for (int cha=dv-du,i=0; cha; cha>>=1,i++)//先跳到同一深度 if(cha&1) vv=fa[vv][i]; if (uu==vv) return uu;//如果u是v的祖先,那他们的LCA肯定就是u了 for (int i=20;i>=0;i--)//不断向上跳 {//因为我们要跳到它们LCA的下面一层,所以它们肯定不相等,如果相等就continue。 if (fa[uu][i]==fa[vv][i]) continue; uu=fa[uu][i]; vv=fa[vv][i]; } return fa[uu][0];//返回父节点 }
加常数优化的:
int LCA(int u, int v) { if(deep[u] < deep[v]) //用数学语言来说就是:不妨设u的深度 >= v的深度 swap(u, v); while(deep[u] > deep[v]) u = fa[u][lg[deep[u]-deep[v]] - 1]; //先跳到同一深度 if(u == v) //如果v是u的祖先,那他们的LCA肯定就是v了 return v; for(int k = lg[deep[u]] - 1; k >= 0; --k) //不断向上跳(lg就是之前说的常数优化) if(fa[u][k] != fa[v][k]) //因为我们要跳到它们LCA的下面一层,所以它们肯定不相等,如果不相等就跳过去。 u = fa[u][k], v = fa[v][k]; return fa[u][0]; //返回父节点 }
完整的求17和18的LCA的路径:
u:17−>10−>7(LCA下面一层) −>3
v:18−>16(此时与)−>8−>5(LCA下面一层) −>3
解释:首先,18要跳到和17深度相同,然后18和17一起向上跳,一直跳到LCA的下一层(17是7,18是5),此时LCA就是它们的父亲3。
⒊基于RMQ的在线查询算法。
该算法借助于DFS时的访问次序和RMQ的快速查询。
设depth[]记录每个点的深度,r[]记录每个点在DFS过程中第一次被访问的次序。
刘汝佳的黑书上对此算法作了详细的介绍,当时读的时候有一句“由于每条边被访问了两次,因此一共记录了2n-1个节点”始终想不明白,后来发现在DFS的递归和回溯过程中,对于一个出度为X的点,肯定会被访问X+1次,1次在递归过程中,X在回溯过程中。又因为在一棵树中除根节点外,每个节点的入度均为1,故入度总和为n-1,又有入度 == 出度,所有所有的节点一共被访问了n+n-1次,n次在递归过程中,n-1次在回溯过程中。
设r[u] < r[v] , point[2n-1]里面存放了DFS过程中一次被访问的节点。则在point[ r[u] ]到 point[ r[v] ](包括两端点)之间深度最小的那个点即为两点的LCA,深度最小的点有且仅有一个。此时可分为两种情况,一种是u即为u和v的LCA,第二种就是第三点w是u,v的LCA。
第一种情况中显然v在一棵以u为根节点的子树上,此时显然在DFS过程中先u先放入point[],然后在DFS遍历这个子树的过程中v放入point[],所以在[ r[u] , r[v] ] 中 u即为深度最小的那个点。
第二种情况中DFS过程中必先会遍历完其中一个点所在的子树,然后会回溯到某一节点w继续DFS遍历该节点的其他子树,如果v在此时遍历的子树上,则w即为u,v的LCA。由上可知,point[]的[ r[u] , r[v] ] 区间内必有w。
区间内的快速查询可以用到RMQ或者线段树,这里就不再赘述。
————————————————
版权声明:本文为CSDN博主「自在_飞花」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/zmx354/article/details/18076975
该算法的思想为,按照欧拉序存储结点的深度,则 LCA(u,v) 就是欧拉序上 u 所在位置到 v 所在位置区间上的最小值,这可以用 ST 表来解决。
-
标签:strong data i++ 存在 算法 进制 image 最近公共祖先 最小
原文地址:https://www.cnblogs.com/jiamian/p/12749397.html