标签:marker 标准 html values encoding tuple ict das min
一.主题式网络主题式网络爬虫设计方案
1.爬虫名称:爬取城市GDP排名
2.爬虫爬取的内容:爬取城市GDP排名
3.网络爬虫设计方案概述:
实现思路:在浏览器 中通过F12访问网页源代码,,分析网站源代码,找到自己所需要的数据所在的位置,提取数据,对数据进行保存数据,再对数据进行清洗和处理,数据分析与可视化处理
技术难点:对库使用和库中函数的运用,爬取的内容的机构分析处理
二、主题页面的结构特征分析
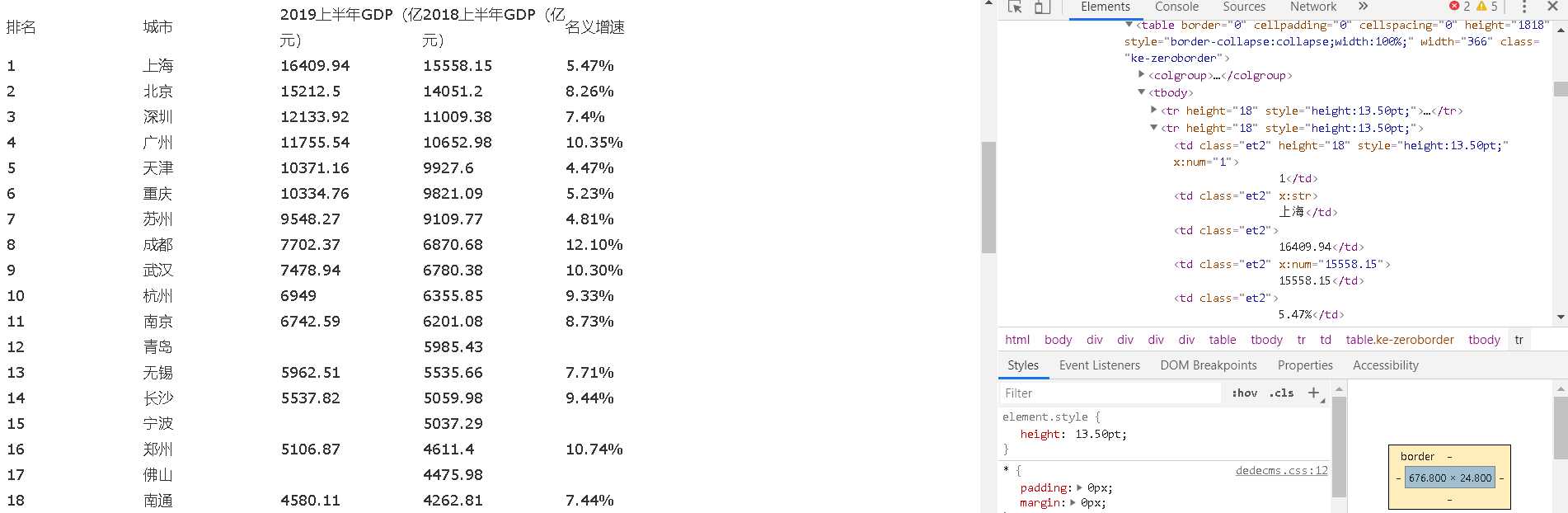
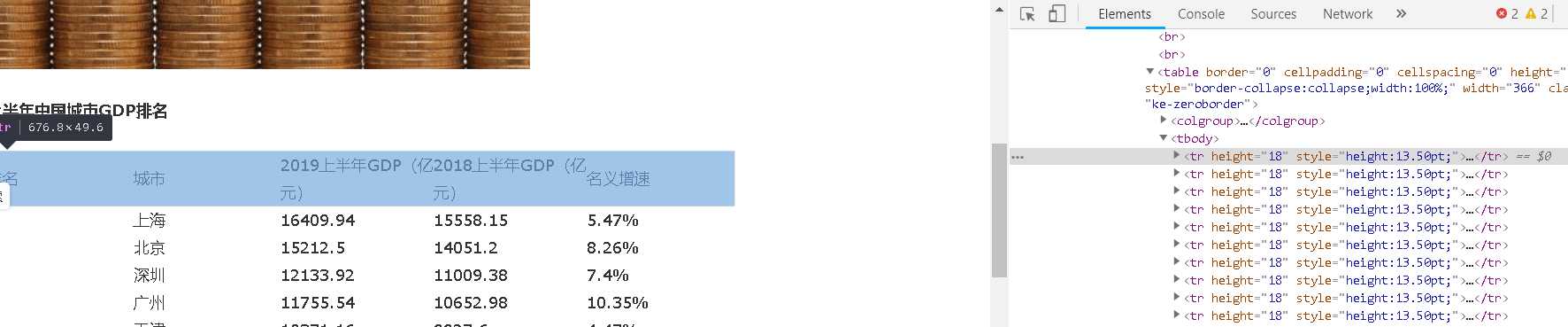
主题页面的结构与特征分析:通过页面的结构分析,可以得到各个数据之间的便签都有关联的关系,城市标签分布在<td class="et2" style="width:54.00pt;" width="72" x:str="">城市</td>
中,排名标签分布<td class="et2" height="18" style="height:13.50pt;width:54.00pt;" width="72" x:str="">排名</td>中,19年GDP标签分布在<td class="et2" style="width:56.25pt;" width="75"x:str="">2019上半年GDP(亿元)</td>中,18年GDP标签分布在<td class="et2" style="width:56.25pt;" width="75" x:str="">2018上半年GDP(亿元)</td>中,名义增速标签分布在<td class="et2" style="width:54.00pt;" width="72" x:str="">名义增速</td>中。各个值则在<tr height="18" style="height:13.50pt;">这种形式中。
三、网络爬虫程序设计
1.数据爬取与采集
import requests from lxml import etree import pandas as pd #爬取2019年上半年中国前10名城市 #伪装爬虫 headers = {‘User-Agent‘:‘Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/70.0.3538.102 Safari/537.36 Edge/18.18362‘} url = "http://www.860816.com/aricle.asp?id=1785" r = requests.get(url,headers = headers) #发送get请求 r.encoding=r.apparent_encoding #构建一个xpath解析对象 html = etree.HTML(r.text) #利用etree.HTML()将html字符串转化为element对象,element对象是xpath语法的使用对象,element对象可由html字符串转化 table = html.xpath("//table[@class=‘ke-zeroborder‘]/tbody") a=[] b=[] c=[] d=[] e=[] lt=[] for td in table: number = td.xpath(".//td[@class=‘et2‘][1]/text()")[1:11] name = td.xpath(".//td[@class=‘et2‘][2]/text()")[1:11] s2019GDP = td.xpath(".//td[@class=‘et2‘][3]/text()")[1:11] #2019上半年GDP(亿元) s2018GDP = td.xpath(".//td[@class=‘et2‘][4]/text()")[1:11] increase1_3 = td.xpath(".//td[@class=‘et2‘][5]/text()")[1:3] increase2_10 = td.xpath(".//td[@class=‘et3‘]/text()")[0:8] for i in range(10): a.append(number[i].strip())#用append生成多维数组 b.append(name[i].strip()) c.append(s2019GDP[i].strip()) d.append(s2018GDP[i].strip()) for i in range(2): e.append(increase1_3[i].strip()) for i in range(8): e.append(increase2_10[i].strip()) e[2],e[1] = e[1],e[2] lt=[] for i in range(10): lt.append([a[i],b[i],c[i],d[i],e[i]]) df=pd.DataFrame(lt,columns=["排名","城市","一九上半年GDP","一八上半年GDP","名义增速"]) print(df) df.to_csv(‘上半年中国前十名城市GDP排名.csv‘,encoding = ‘gbk‘) #保存文件,数据持久化
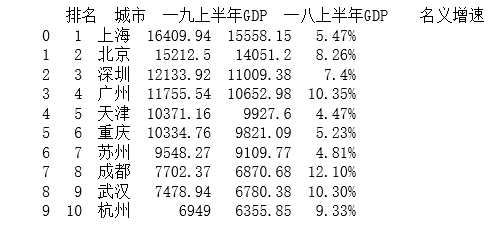
成功保存csv文件
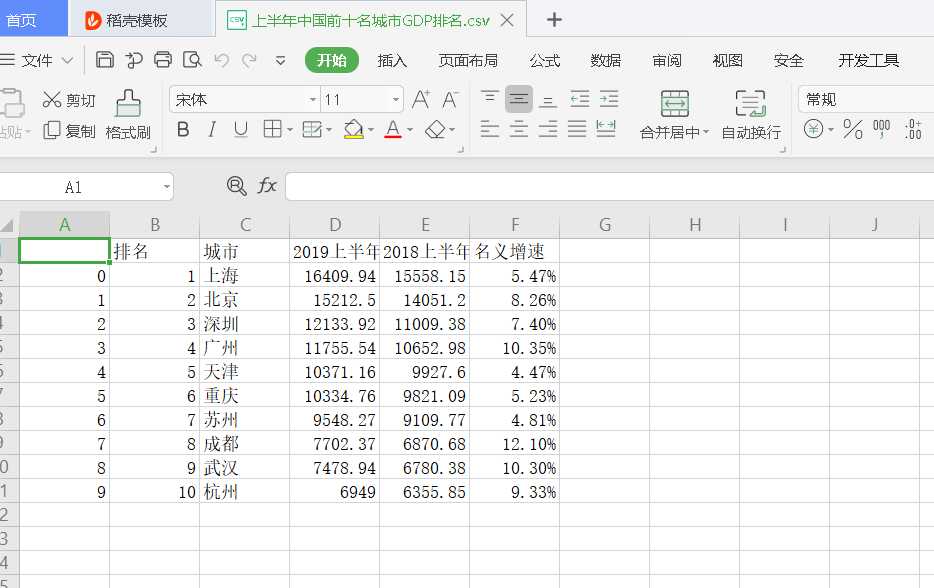
2.进行数据清洗和处理
import pandas as pd #读取csv文件 df = pd.DataFrame(pd.read_csv(‘上半年中国前十名城市GDP排名.csv‘,engine=‘python‘)) df
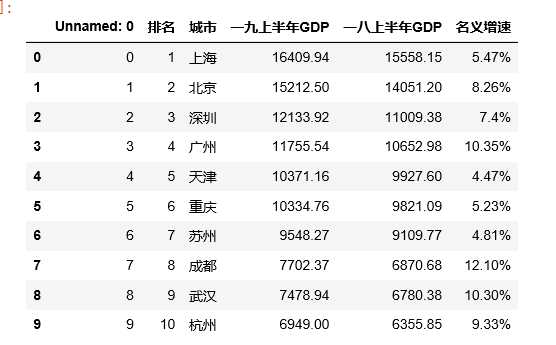
#删除无效列 df.drop(‘名义增速‘,axis=1,inplace=True) df.drop(‘城市‘,axis=1,inplace=True) df.drop(‘一八上半年GDP‘,axis=1,inplace=True) df.head()#表示前五行
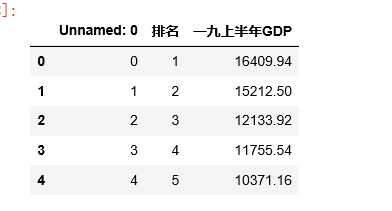
#缺失值处理 df[df.isnull().values==True]#返回无缺失值

#检查是否有重复值 df.duplicated()

#使用describe查看统计信息 df.describe()
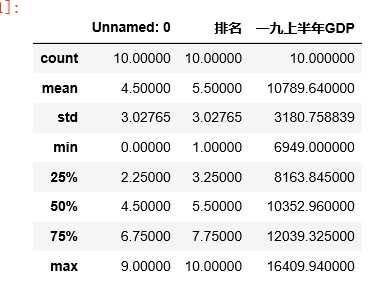
#数据维度 print(‘---数据维度:{:}行{:}列---\n‘.format(df.shape[0],df.shape[1]))
df.info()#查看各列数据类型

#数据分析 from sklearn.linear_model import LinearRegression#线性回归算法 X = df.drop("一九上半年GDP",axis=1) predict_model = LinearRegression()#线性回归模型 predict_model.fit(X,df[‘一九上半年GDP‘])#fit() 用来分析模型参数 print("回归系数为:",predict_model.coef_)#predict() 是通过 fit() 算出的模型参数构成的模型,对解释变量进行预测获得的值

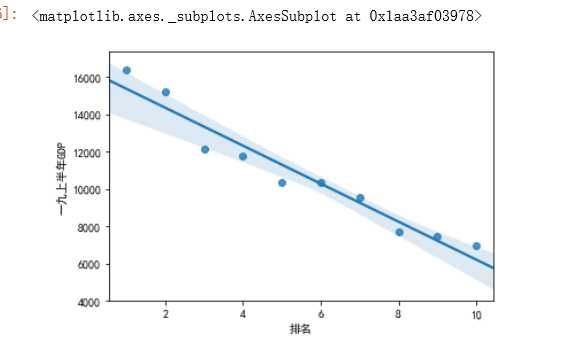
#绘制排名与一九上半年GDP的回归图 sns.regplot(df.排名,df.一九上半年GDP)
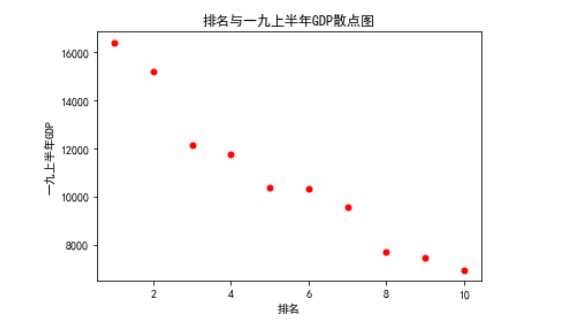
#画出散点图 def siger(): plt.scatter(df.排名, df.一九上半年GDP, color=‘red‘, s=25, marker="o") plt.xlabel("排名") plt.ylabel("一九上半年GDP") plt.title("排名与一九上半年GDP散点图") plt.show() siger()
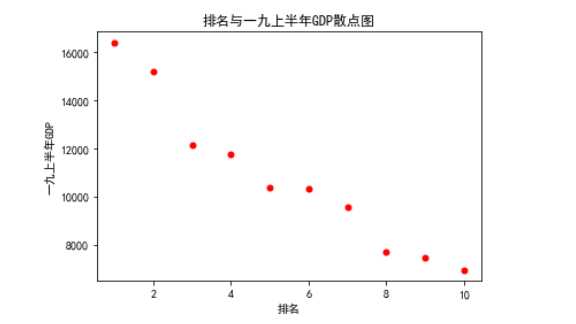
# 绘制柱状图 def algd(): x = df[‘排名‘] y = df[‘一九上半年GDP‘] plt.xlabel(‘排名‘)#设置横坐标名 plt.ylabel(‘一九上半年GDP‘)#设置纵坐标名 plt.bar(x,y)#柱状图 plt.title("绘制排名与一九上半年GDP条形图") plt.show() algd()
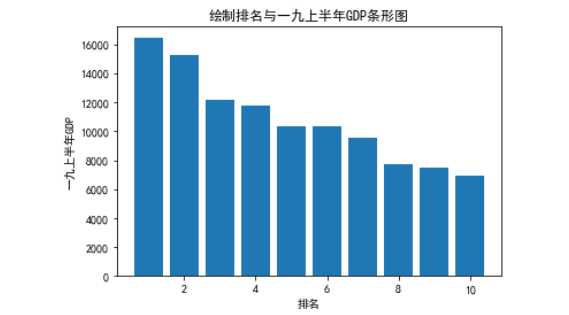
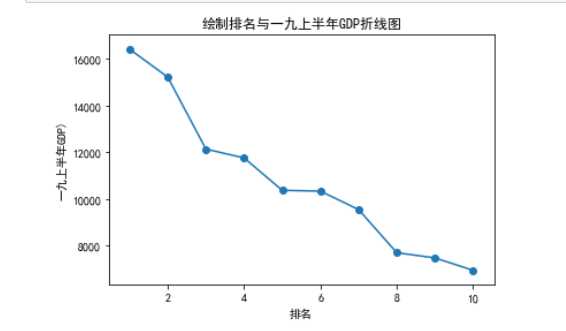
#绘制折线图 def mei(): x = df[‘排名‘] y = df[‘一九上半年GDP‘] plt.xlabel(‘排名‘) plt.ylabel(‘一九上半年GDP)‘) plt.plot(x,y)#画折线图 plt.scatter(x,y)#画散点 plt.title("绘制排名与一九上半年GDP折线图")#标题 plt.show() mei()
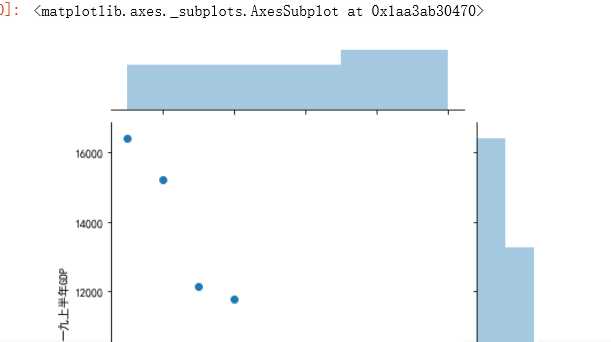
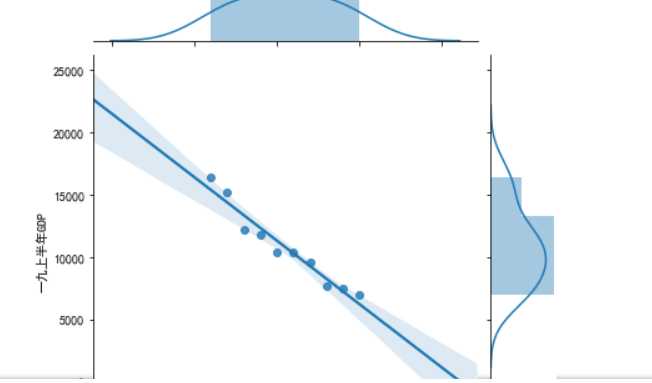
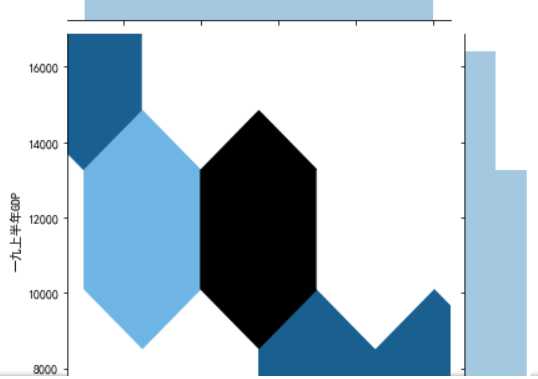
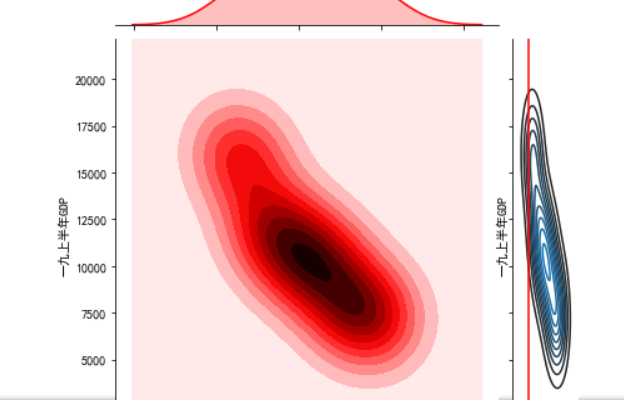
#绘制分布图 sns.jointplot(x="排名",y=‘一九上半年GDP‘,data = df)#设置xy轴,显示columns名称 sns.jointplot(x="排名",y=‘一九上半年GDP‘,data = df, kind=‘reg‘) sns.jointplot(x="排名",y=‘一九上半年GDP‘,data = df, kind=‘hex‘)#kind 设置类型:scatter reg resid kde(密度图) hex(六边形) sns.jointplot(x="排名",y=‘一九上半年GDP‘,data = df, kind=‘kde‘, color=‘r‘)#设置颜色 sns.kdeplot(df[‘排名‘], df[‘一九上半年GDP‘])
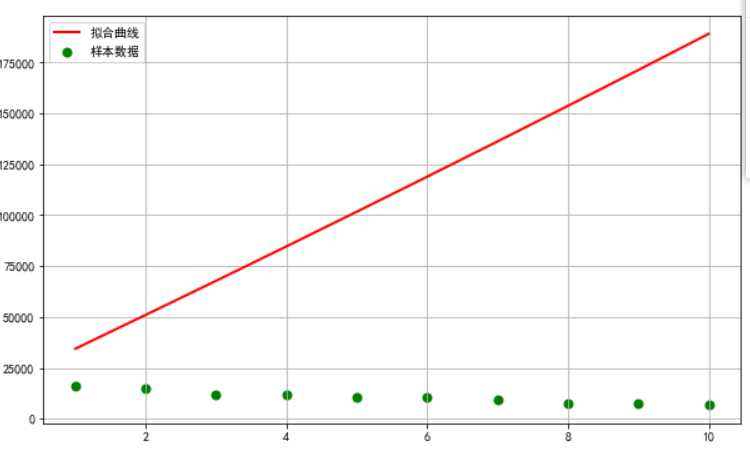
#一元一次回归方程 import matplotlib from scipy.optimize import leastsq from numpy import genfromtxt #读入样本文件,需转换成数组(列表)形式 df=genfromtxt(‘上半年中国前十名城市GDP排名.csv‘,dtype=float,delimiter=‘,‘)#因为导入的是csv文件,所以用‘,’分隔 DF=np.delete(df,0,axis=0) Y=DF[:,3]#直接提取数组第3列数据,转换成一维数组 X=DF[:,1] #fit_func函数,指出了代拟合函数的函数形状 def fit_func(p,x): k,b=p return k*x+b #误差函数,即拟合函数所成的值与实际值得差 def error_func(p,x,y): return fit_func(p,x)-y#(x,y)#模拟值 #y样本值 p0=[0,0]#初始值 #读取leastsq返回值结果,leastsq的返回值是一个tuple Para=leastsq(error_func,p0,args=(X,Y))#arg参数 ,样本数据(X和Y数组) #ParaPara返回的值(参数) k,b=Para[0]#一元方程系数返回值 plt.figure(figsize=(10,6)) plt.scatter(X,Y,color="green",label=u"样本数据",linewidth=2) x=np.linspace(1,10,10) y=a*x*x+b*x+c plt.plot(x,y,color="red",label=u"拟合曲线",linewidth=2) plt.legend()#绘制拟合直线 plt.grid()#生成网格 plt.show()
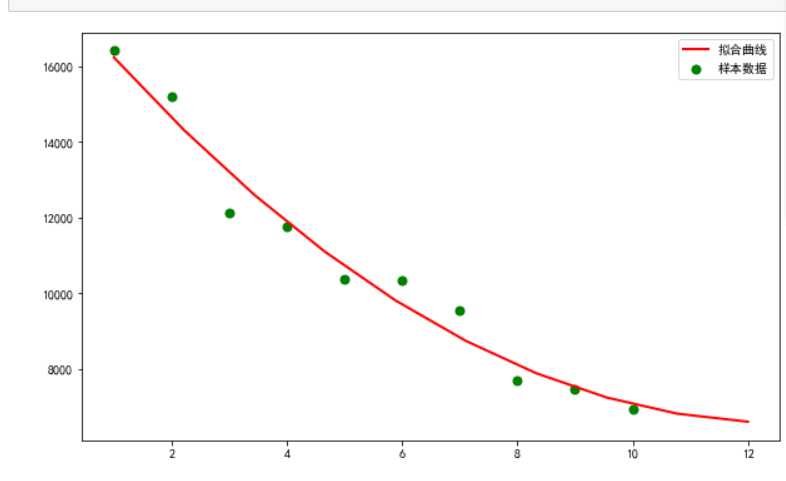
#一元二次回归方程 import matplotlib from scipy.optimize import leastsq from numpy import genfromtxt df=genfromtxt(‘上半年中国前十名城市GDP排名.csv‘,dtype=float,delimiter=‘,‘) DF=np.delete(df,0,axis=0) Y=DF[:,3] X=DF[:,1] #二次函数的标准形式 def fit_func(p,x): a,b,c=p return a*x*x+b*x+c def error_func(p,x,y): return fit_func(p,x)-y p0=[0,0,0] Para=leastsq(error_func,p0,args=(X,Y)) a,b,c=Para[0] #画样本点(散点) plt.figure(figsize=(10,6))#定义画布大小 plt.scatter(X,Y,color="green",label=u"样本数据",linewidth=2)#scatter表示画散点图 #画拟合直线 x=np.linspace(1,12,10)#生成10个点 y=a*x*x+b*x+c plt.plot(x,y,color="red",label=u"拟合曲线",linewidth=2) plt.legend()#绘制拟合直线 plt.show()
5.将以上各部分的代码汇总,附上完整程序代码
import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy.optimize import leastsq import seaborn as sns import scipy as sp import seaborn as sns # 用来正常显示中文标签 plt.rcParams[‘font.sans-serif‘] = [‘SimHei‘] # 用来正常显示负号 plt.rcParams[‘axes.unicode_minus‘] = False import requests from lxml import etree import pandas as pd #爬取2019年上半年中国前10名城市 #伪装爬虫 headers = {‘User-Agent‘:‘Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/70.0.3538.102 Safari/537.36 Edge/18.18362‘} url = "http://www.860816.com/aricle.asp?id=1785" r = requests.get(url,headers = headers) #发送get请求 r.encoding=r.apparent_encoding #构建一个xpath解析对象 html = etree.HTML(r.text) #利用etree.HTML()将html字符串转化为element对象,element对象是xpath语法的使用对象,element对象可由html字符串转化 table = html.xpath("//table[@class=‘ke-zeroborder‘]/tbody") a=[] b=[] c=[] d=[] e=[] lt=[] for td in table: number = td.xpath(".//td[@class=‘et2‘][1]/text()")[1:11] name = td.xpath(".//td[@class=‘et2‘][2]/text()")[1:11] s2019GDP = td.xpath(".//td[@class=‘et2‘][3]/text()")[1:11] #2019上半年GDP(亿元) s2018GDP = td.xpath(".//td[@class=‘et2‘][4]/text()")[1:11] increase1_3 = td.xpath(".//td[@class=‘et2‘][5]/text()")[1:3] increase2_10 = td.xpath(".//td[@class=‘et3‘]/text()")[0:8] for i in range(10): a.append(number[i].strip())#用append生成多维数组 b.append(name[i].strip()) c.append(s2019GDP[i].strip()) d.append(s2018GDP[i].strip()) for i in range(2): e.append(increase1_3[i].strip()) for i in range(8): e.append(increase2_10[i].strip()) e[2],e[1] = e[1],e[2] lt=[] for i in range(10): lt.append([a[i],b[i],c[i],d[i],e[i]]) df=pd.DataFrame(lt,columns=["排名","城市","一九上半年GDP","一八上半年GDP","名义增速"]) print(df) df.to_csv(‘上半年中国前十名城市GDP排名.csv‘,encoding = ‘gbk‘) #保存文件,数据持久化 import pandas as pd #读取csv文件 df = pd.DataFrame(pd.read_csv(‘上半年中国前十名城市GDP排名.csv‘,engine=‘python‘)) df #删除无效列 df.drop(‘名义增速‘,axis=1,inplace=True) df.drop(‘城市‘,axis=1,inplace=True) df.drop(‘一八上半年GDP‘,axis=1,inplace=True) df.head()#表示前五行 #缺失值处理 df[df.isnull().values==True]#返回无缺失值 #检查是否有重复值 df.duplicated() #使用describe查看统计信息 df.describe() #数据维度 print(‘---数据维度:{:}行{:}列---\n‘.format(df.shape[0],df.shape[1])) df.info()#查看各列数据类型 #绘制排名与一九上半年GDP的回归图 sns.regplot(df.排名,df.一九上半年GDP) #画出散点图 def siger(): plt.scatter(df.排名, df.一九上半年GDP, color=‘red‘, s=25, marker="o") plt.xlabel("排名") plt.ylabel("一九上半年GDP") plt.title("排名与一九上半年GDP散点图") plt.show() siger() # 绘制柱状图 def algd(): x = df[‘排名‘] y = df[‘一九上半年GDP‘] plt.xlabel(‘排名‘)#设置横坐标名 plt.ylabel(‘一九上半年GDP‘)#设置纵坐标名 plt.bar(x,y)#柱状图 plt.title("绘制排名与一九上半年GDP条形图") plt.show() algd() #绘制折线图 def mei(): x = df[‘排名‘] y = df[‘一九上半年GDP‘] plt.xlabel(‘排名‘) plt.ylabel(‘一九上半年GDP)‘) plt.plot(x,y)#画折线图 plt.scatter(x,y)#画散点图 plt.title("绘制排名与一九上半年GDP折线图")#标题 plt.show() mei() #绘制分布图 sns.jointplot(x="排名",y=‘一九上半年GDP‘,data = df)#设置xy轴,显示columns名称 sns.jointplot(x="排名",y=‘一九上半年GDP‘,data = df, kind=‘reg‘) sns.jointplot(x="排名",y=‘一九上半年GDP‘,data = df, kind=‘hex‘)#kind 设置类型:scatter reg resid kde(密度图) hex(六边形) sns.jointplot(x="排名",y=‘一九上半年GDP‘,data = df, kind=‘kde‘, color=‘r‘)#设置颜色 sns.kdeplot(df[‘排名‘], df[‘一九上半年GDP‘]) #一元一次回归方程 import matplotlib from scipy.optimize import leastsq from numpy import genfromtxt #读入样本文件,需转换成数组(列表)形式 df=genfromtxt(‘上半年中国前十名城市GDP排名.csv‘,dtype=float,delimiter=‘,‘)#因为导入的是csv文件,所以用‘,’分隔 DF=np.delete(df,0,axis=0) Y=DF[:,3]#直接提取数组第3列数据,转换成一维数组 X=DF[:,1] #fit_func函数,指出了代拟合函数的函数形状 def fit_func(p,x): k,b=p return k*x+b #误差函数,即拟合函数所成的值与实际值得差 def error_func(p,x,y): return fit_func(p,x)-y#(x,y)#模拟值 #y样本值 p0=[0,0]#初始值 #读取leastsq返回值结果,leastsq的返回值是一个tuple Para=leastsq(error_func,p0,args=(X,Y))#arg参数 ,样本数据(X和Y数组) #ParaPara返回的值(参数) k,b=Para[0]#一元方程系数返回值 plt.figure(figsize=(10,6)) plt.scatter(X,Y,color="green",label=u"样本数据",linewidth=2) x=np.linspace(1,10,10) y=a*x*x+b*x+c plt.plot(x,y,color="red",label=u"拟合曲线",linewidth=2) plt.legend()#绘制拟合直线 plt.grid()#生成网格 plt.show() #一元二次回归方程 import matplotlib from scipy.optimize import leastsq from numpy import genfromtxt df=genfromtxt(‘上半年中国前十名城市GDP排名.csv‘,dtype=float,delimiter=‘,‘) DF=np.delete(df,0,axis=0) Y=DF[:,3] X=DF[:,1] #二次函数的标准形式 def fit_func(p,x): a,b,c=p return a*x*x+b*x+c def error_func(p,x,y): return fit_func(p,x)-y p0=[0,0,0] Para=leastsq(error_func,p0,args=(X,Y)) a,b,c=Para[0] #画样本点(散点) plt.figure(figsize=(10,6))#定义画布大小 plt.scatter(X,Y,color="green",label=u"样本数据",linewidth=2)#scatter表示画散点图 #画拟合直线 x=np.linspace(1,12,10)#生成10个点 y=a*x*x+b*x+c plt.plot(x,y,color="red",label=u"拟合曲线",linewidth=2) plt.legend()#绘制拟合直线 plt.show()
标签:marker 标准 html values encoding tuple ict das min
原文地址:https://www.cnblogs.com/FFDXMM/p/12759620.html