学习记录：二叉树

标签：深度优先遍历   数组   理解   后序   推荐   这一   lang   net   指针   

二叉树

二叉树的性质

每个节点最多都有两个子节点的树称为二叉树。其性质与定义有：

• 第\(i\)层最多有\(2^{i-1}\)个节点
• 满二叉树：若每一层的节点数都是满的（都为\(2^{i-1}\)），则为满二叉树
• 完全二叉树：一棵满二叉树只在最后一层有缺失，则称为完全二叉树

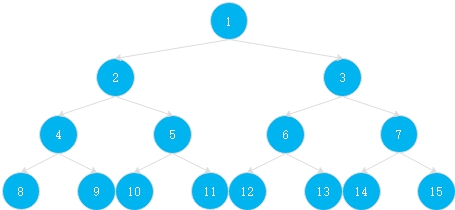
而对于完全二叉树，它的子节点与父结点还有一种性质

• 对于编号为\(i\)的节点，其父节点为\(i/2\)

• 如果编号为\(i\)的节点有子节点，则其左节点编号为\(2i\)与\(2i+1\)

  PS：编号从1开始

二叉树的储存

一般用指针，和链表同理

struct node{
	int value;
	node *l,*r;
};

用数组也可以，而且能更为直观的表现完全二叉树中子节点与父节点的关系，但是要注意编号从1开始

二叉树的遍历

先用数组模拟来实现遍历，这里设二叉树为 int num[]={-1,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15};

广度优先遍历

void BFS(int start)
{
	queue<int> q;
	q.push(start);
	cout<<num[start]<<" ";
	while (!q.empty()){
		int t1=q.front()*2,t2=q.front()*2+1;
		if (t1<16){
			q.push(t1);
			cout<<num[t1]<<" ";
		}
		if (t2<16){
			q.push(t2);
			cout<<num[t2]<<" ";
		}
		q.pop();
	}
}

深度优先遍历

深度遍历一颗二叉树共有三种方式

• 先序遍历：按父节点->左儿子->右儿子的顺序遍历
• 中序遍历：按左儿子->父节点->右儿子的顺序遍历
• 后序遍历：按左儿子->右儿子->父节点的顺序遍历

【数据结构】理解二叉树的三种遍历--前序、中序、后序 +层序（简明易懂）强烈推荐这一篇，这一篇博客写的非易懂

不难发现三种遍历其实就互相调整了一下顺序，用递归可以很简单的实现

void preorder(int root)
{
	if (root>16)
		return ;
	cout<<num[root]<<‘ ‘;
	preorder(root*2);
	preorder(root*2+1);
}
void inorder(int root)
{
	if (root>16)
		return ;
	inorder(root*2);
	cout<<num[root]<<‘ ‘;
	inorder(root*2+1);
}
void postorder(int root)
{
	if (root>16)
		return ;
	postorder(root*2);
	postorder(root*2+1);
	cout<<num[root]<<‘ ‘;
}

如果是用指针实现的，那么把退出条件改一下，root*2替换为左指针，root*2+1替换为右指针即可

学习记录：二叉树

标签：深度优先遍历   数组   理解   后序   推荐   这一   lang   net   指针   

原文地址：https://www.cnblogs.com/Salty-Fish/p/12760772.html