标签:https mamicode 思考 情况 -- image 存在 src 概念
最近在学习高数内容,之前的学习都是应付式,现在准备深一点研究。
从我们人的直接来说,如果一条线段是连续的,那它必然是光滑且没有断裂。
(1)函数连续的定义
但是高数中,函数的连续定义如下:

可以看出,高等数学中,对连续是针对点而言的,也就是说,如果你要说明某个范围内,函数连续,那么它必须在这个范围内每一个点都得符合上述定义。
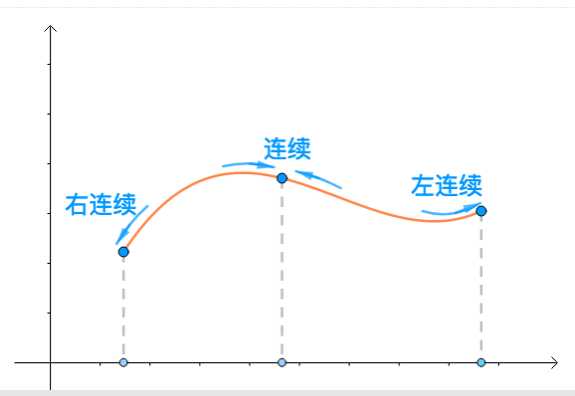
也就是说,左极限=右极限=该点函数值,则该点连续。
(2)函数间断的定义分成下面三种情况
情况1:
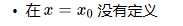
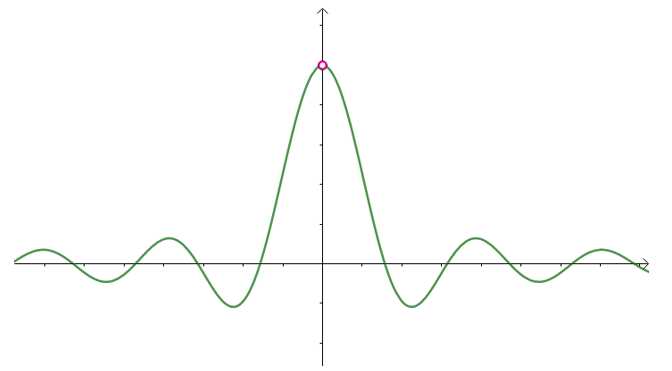
函数在圆圈处没有定义,该点为间断点。
情况2:
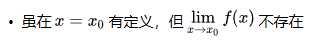
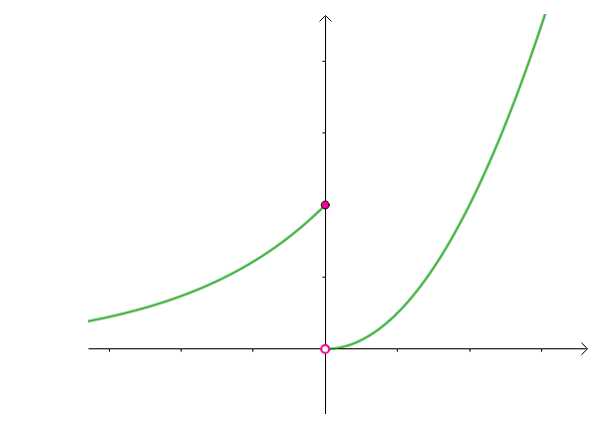
因为左极限不等于右极限,所以该点极限不存在,该点为间断点。
情况3:
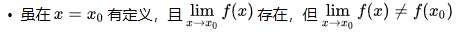
左右极限存在,所以该点有极限,但是该点极限与函数该点值不等,所以该点为间断点。
上述说明的间断点都存在左右极限,所以数学上把左右极限存在的这种间断点统一称为第一类间断点
除了第一类间断点,其它的都是第二类间断点。

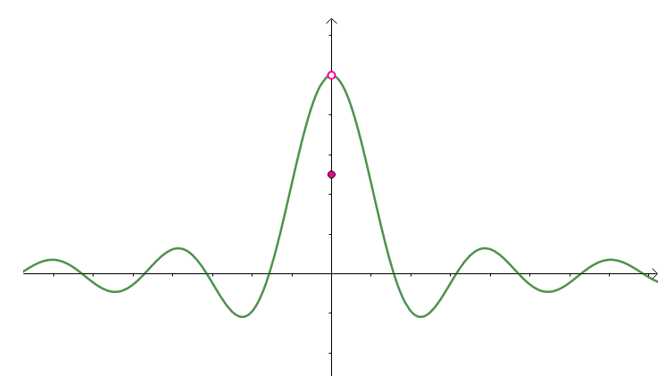
下面贴几张第二类间断点的图像:
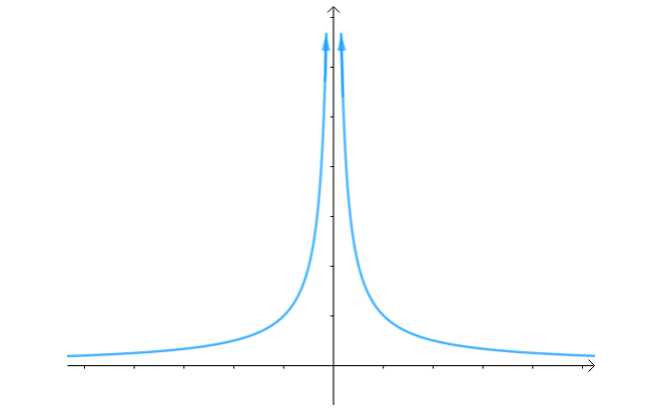
左右极限不存在,第二类间断点
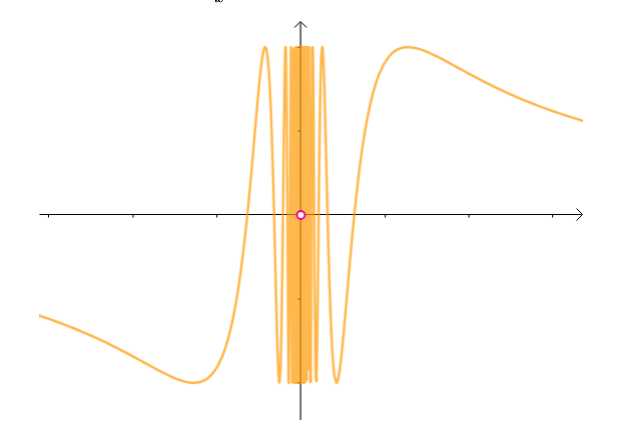
该函数来回波动,没有极限,第二类间断点
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------看了连续的基本概念和间断的基本定义,那么来思考这道题:

看一下它的图像:
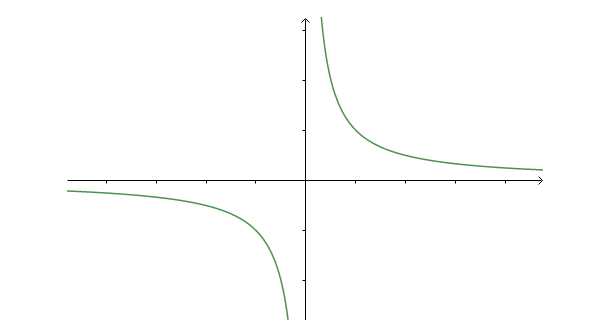
猛然一看是不是觉得它间断了?没错的确是间断了,那它间断点是哪个,一眼就看出是0了。
那它是不是连续函数呢?我们固有的思维都认为,连续一定是光滑的,不间断的。但是我告诉你它是连续函数,连续,连续,连续!
为什么呢?你回头去看看函数连续的定义。首先要明确函数的取值范围,由于(1/x)在0没有意义,固然在0无定义,所以取值范围排除0,然后再观察函数图像,它处处连续。
所以它是连续函数。
结论:说白了,当讨论一个函数是不是连续,首先得明确函数连续的定义。而看一个函数是否间断,你可以不用去看函数在某点是否有定义,你直接观察它是否间断了就好。
所以函数连续,可能有间断点。你也可以直接认为,函数连续与它是否有间断点没有关系。也就是一个函数连续可能有间断点,有间断点的函数可能是连续函数。
标签:https mamicode 思考 情况 -- image 存在 src 概念
原文地址:https://www.cnblogs.com/hmy-666/p/12765619.html