标签:alt 最小花费 sim out 差分 arc 高效 class 差分约束
只有左右边着地的拼图可以作为一个连通块的开头和结尾,不着地的拼图只能相互拼接,可以正负号建点区分左右,然后建图。
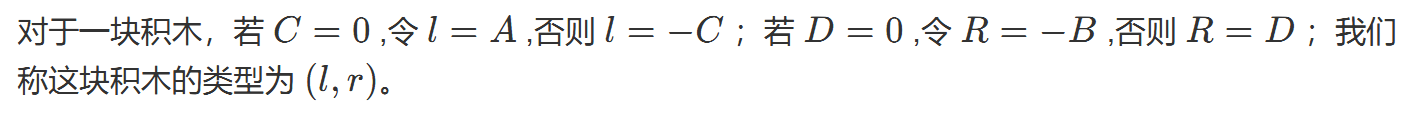
一个合法的连通块就是一条起点编号大于0,终点编号小于0的路径,图可以合法拆分的充要条件就是:
不妨把序列异或和放在第\(n+1\)个位置,问题转化成每次可以交换一个位置和第\(n+1\)个位置的数字,问最少几次可以让\(a,b\)序列前\(n\)个数相同。
显然新序列里只要有一个数值单独出现,异或和也会单独出现,那么无解。
考虑建图求解最小值,把\(a_i\)和\(b_i\)连边,对于一个连通块,需要边数次交换次数才能完成换位。不同的连通块之间还需一次额外的切换,那么答案就是\(n+k\),\(k\)为连通块个数。如果第\(n+1\)个数一开始就在某个连通块里,那么答案还需减一。
只需向横纵坐标相邻点连边即可,因为这样连边和暴力连边连通性,权值都是一样的。
求最小生成树。
显然只保留两条路径即可,预处理最短路,用最短路更新一下答案,\(n^2\)枚举路径交,再更新一下答案即可。
枚举删边再拓扑判环会超时,可以考虑拓扑判环的过程,允许其有一次入度唯一就可以进队的机会就相当于删了一条边,那么只需枚举点即可。
将两类边分别处理连通块编号,如果两个点在两类边中都属于通一个连通块就符合题意,用一下\(\mathrm{map}\)就好了。
考虑\(\mathrm{Kruskal}\)算法的过程,按边权从小到大的顺序加边,那么路径瓶颈边就是最小生成树上的路径最大边,朴素算法树上倍增什么的。
考虑优化,可以直接把\(\mathrm{Kruskal}\)过程中的边权赋成点权,建点来保证连通性,其实就是\(\mathrm{Kruskal}\)重构树。那么问题转换成\(\mathrm{LCA}\),使用一些高效率的\(\mathrm{RMQ}\)算法即可。
考虑一条新建道路对树边的贡献,也就是说一条额外边可以贡献树上一条路径的答案,用线段树维护一下就好了。
考虑\(\mathrm{Kruskal}\),已经联通的连通块里随意加入尽可能大的边即可。
将其看做\(n+1\)个点,询问\(c[i,j]\)就是将\(s[i-1],s[j]\)两点变为有联系的,使所有点联通,最小生成树。
首先跑最小生成树让\(B\)尽量小,那么答案要么在最小生成树里,要么是两个点权很大的点,直接\(n^2\)枚举就好了。
设答案\(\mathrm{ans}=\prod p_i^{\alpha _i}\),一个生成树边权的最小公倍数为\(v_T\),那么对于质因子\(p_i\),其\(\alpha_i\)在答案中的贡献就是所有生成树权\(v_T\)中因子\(p_i\)指数最大值。
而生成树权\(v_T\)中因子\(p_i\)指数最大值又取决于所有边权\(p_i\)因子的指数最小值。那么我们可以对每一个质因子\(p\)用每条边权上的指数跑最大生成树,根据最大生成树的性质,可以保证最小边权最大,那么乘到答案里就可以了。
需要注意常数优化,每次重新建图只取边权因子有\(p\)的边即可。
直接判重边建图会超时,考虑对于点对\((x,y)\)之间有\((u_i,v_i)(i=1\sim x)\)这么多条备选的边,可以设最小边权为\(f\),有\(f=\min_{i=1}^x\{k_1u_i+k_2v_i\}\),设最优决策为\(t\),有\(f=k_1u_t+k_2v_t\),化成直线方程的形式:\(v_t=-\frac{k_1}{k_2}u_t+\frac{f}{k_2}\)。
也就是说\(t\)是让一条斜率为\(-\frac{k_1}{k_2}\)切,得到截距最小的点,可以对每一条边维护一个凸壳,然后二分找切点。
把询问按照斜率排序,优化掉一个\(\log\)就可以过了。
二分答案,\(\mathrm{SPFA}\)判负环。
设\(f_{x,y,k}\)代表\(x\sim y\),经过恰好\(k\)条边,边权不降的最短路,直接排序\(dp\)即可。
列出转移,\(\mathrm{SPFA\ dp}\)即可。
考虑把一条路径上的\(x\)权和\(S_x\)与\(y\)权和\(S_y\)看做一个点的横纵坐标,那么可以通过维护凸壳得知\(a\)取何值是这条路径会成为最短路,然后统计期望。
考虑到大部分点不会在凸壳上,可以用\(\mathrm{SPFA}\)的思想松弛,如果加了一条路径更新了凸壳就进入队列继续尝试更新。
根据题意建图,跑差分约束板子。
根据题意建图,跑差分约束板子。
设\(a_x\)表示第\(x\)行被加了几次,\(b_y\)表示第\(y\)列被加了几次,然后建图跑差分约束。
答案具有单调性,直接二分答案。
设\(d_i\)表示前\(i\)秒释放能量的次数,需要约束三个条件:
\(1.\) 每秒最多释放一次。
\(2.\) 两次释放有间隔\(\mathrm{cd}\)。
\(3.\) 需要保证存活:设到第\(i\)秒位置至少要释放能量\(p\),则\(15p+\mathrm{hp}-S_{a_{i+1}}\geq 1\),解得\(p=\lceil\frac{S_{a_{i+1}}-\mathrm{hp}+1}{15}\rceil\),那么需要保证在时间段\([pos,i]\)里至少释放一次能量。
差分约束即可。
考虑连边\((u,v,w)\),表示点\(u\)的权值比点\(v\)的权值至少大\(w\),那么拓扑序\(\mathrm{dp}\)可以求解。
建图用线段树。
标签:alt 最小花费 sim out 差分 arc 高效 class 差分约束
原文地址:https://www.cnblogs.com/Parsnip/p/12767889.html