标签:mamicode 函数 pre art div alt bre ret stp
定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
暴力解法:
思路:从字符串中选出一个子串,其中子串的开头字符和末尾字符一样,用一个函数Palindrome来判断该子串是否为回文,若是则与max(记录目前为止找到的最长回文的长度)进行比较看最长回文是否要修改;若不是则寻找下一个。
1 class Solution { 2 public: 3 bool Palindrome(string& s,int start,int end) 4 { 5 while(start<=end) 6 { 7 if(s[start]!=s[end]) 8 return false; 9 else 10 { 11 start++;end--; 12 } 13 } 14 return true; 15 } 16 string longestPalindrome(string s) { 17 int start(0);int n=s.size();int end=n-1; 18 int max(0);int maxnew(0);string maxstr=""; 19 while(start<=end) 20 { 21 for(;end>=start;end--) 22 { 23 if(s[end]==s[start]) 24 if(Palindrome(s,start,end))//是回文子串 25 { 26 maxnew=end-start+1; 27 if(maxnew>max)//判断是不是最长 28 { 29 max=maxnew; 30 maxstr=s.substr(start,end-start+1);//是最长则修改 31 //拷贝s从start开始的end-start+1个字符 32 break; 33 } 34 } 35 } 36 start++; 37 end=n-1; 38 } 39 return maxstr; 40 } 41 };
中心扩展法:
思路:
我们知道回文串一定是对称的,所以我们可以每次循环选择一个中心,进行左右扩展,判断左右字符是否相等即可。
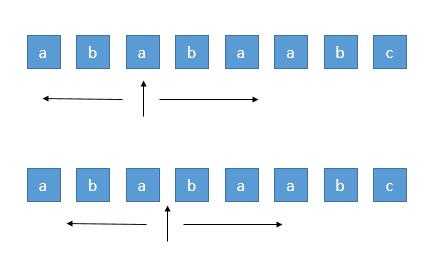
由于存在奇数的字符串和偶数的字符串,所以我们需要从一个字符开始扩展,或者从两个字符之间开始扩展
1 class Solution { 2 public: 3 string longestPalindrome(string s) { 4 int n=s.size(); 5 if(n==0) return ""; 6 int start(0);int max(0);string maxst;int len; 7 for(int i=0;i<n;i++) 8 { 9 int len1=lengthPalindrome(s,i,i); 10 int len2=lengthPalindrome(s,i,i+1); 11 len=len1>len2?len1:len2; 12 if(len>max)//len>max,必定要修改 13 {//选len1、len2中最大的那个来和max比较,看是否要修改最长回文子串 14 if(len1>=len2) 15 { 16 max=len1; 17 start=i-len1/2; 18 maxst=s.substr(start,len1); 19 } 20 else //len2>len1 21 { 22 max=len2; 23 start=i+1-len2/2; 24 maxst=s.substr(start,len2); 25 } 26 } 27 } 28 return maxst; 29 } 30 private: 31 int lengthPalindrome(string& s,int left,int right) 32 { 33 int n=s.size();int ans(1); 34 while(left>=0&&right<n) 35 { 36 if(s[left]==s[right]) 37 { 38 ans=right-left+1; 39 left--;right++; 40 } 41 else break; 42 } 43 return ans; 44 } 45 };
标签:mamicode 函数 pre art div alt bre ret stp
原文地址:https://www.cnblogs.com/cs0915/p/12769969.html