标签：src   log   快速   贪心   string   flag   ref   algo   小根堆   

题目:

题目链接:

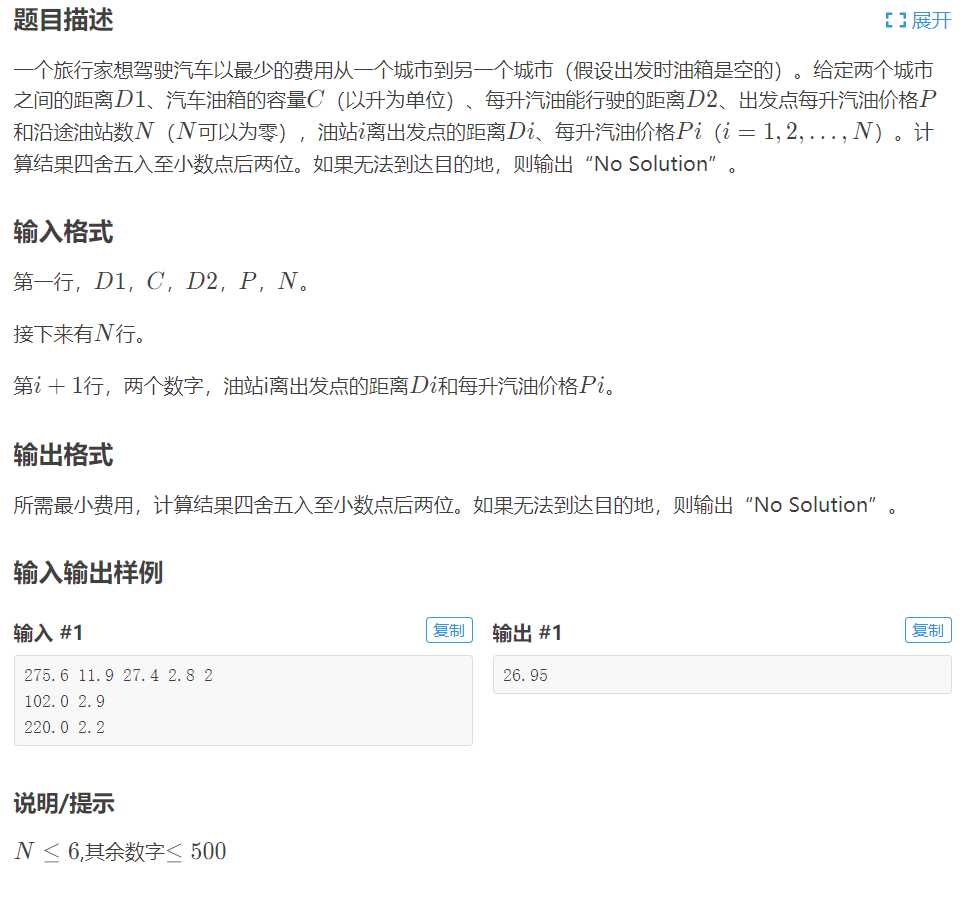
https://www.luogu.com.cn/problem/P1016

考察点:

反悔贪心、思维

侃侃:

这种题目就像是中学的应用题,让你读着读着就崩溃了（当然大佬不会崩溃了，像我
这样的菜鸡就会了，嘻嘻）
我没猜错的话你一定会贪心，就算不会至少也听说过贪心。但是反悔贪心你听过吗？
说白了，反悔贪心就是迷途知返了，虽然我们都很‘贪’,但是如果并不能修成正果，
(达到最优)，那么要的再多都不会有好结果的。
我们都知道,贪心每次取的都是局部最优的结果,这就会导致我们到最后取到的全局
结果不一定是最优的。
而反悔贪心是每次先尝试这去找一个比局部更大一点的最优结果,如果不合适就返回。
找到了及继续往下一步。

反悔贪心的分类:

反悔自动机：

即设计一种反悔策略，使得随便一种贪心策略都可以得到正解。
基本的设计思路是：每次选择直观上最接近全局最优解的贪心策略，若发现最优解不对，就想办法自动支持反悔策略。（这就是自动机的意思）
具体题目具体分析。一般需要反悔自动机的题都是通过差值巧妙达到反悔的目的。

反悔堆：

即通过堆（大根堆、小根堆）来维护当前贪心策略的最优解，若发现最优解不对，就退回上一步，更新最优解。
由于堆的性质，使得堆的首数据一定是最优的，这就可以实现快速更新最优解。

关于本题:

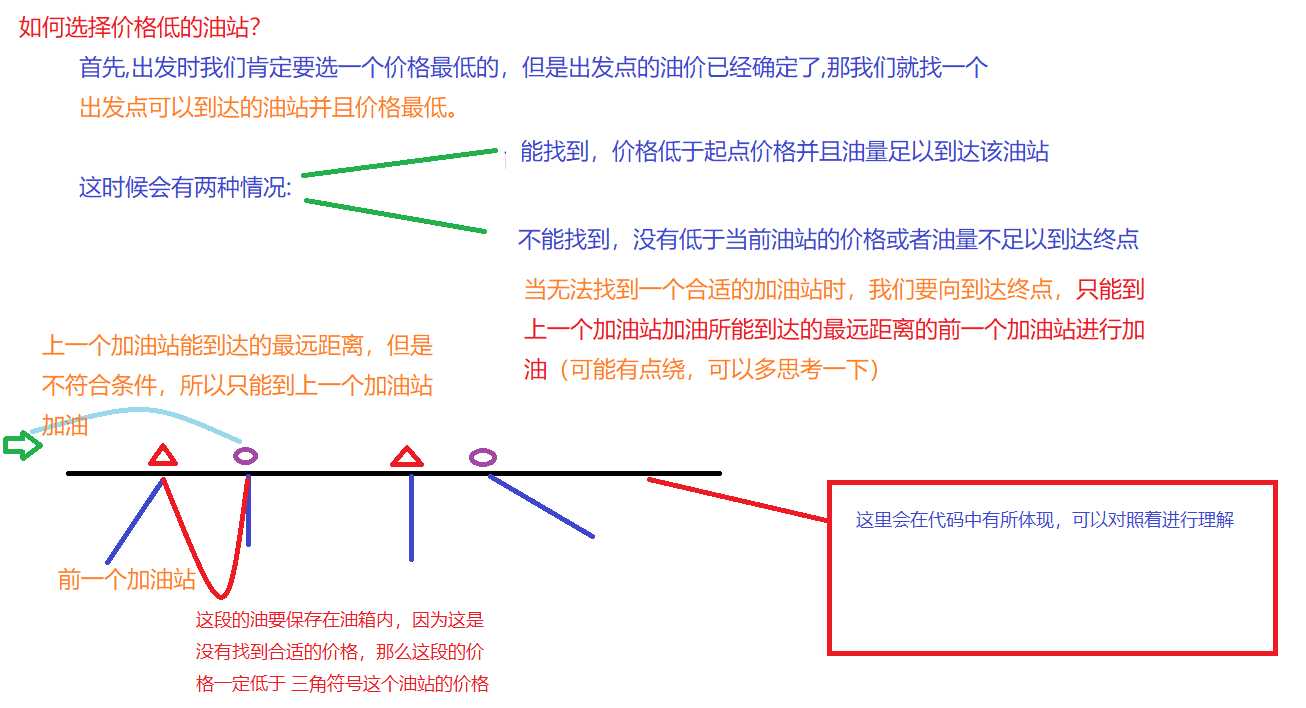
我们发现要使得最后的花费尽可能的最小,我们的油价只要一直保持着较低的价格并且能够到达
目的地即可。

Code:

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 505;

typedef long long LL;

double price[maxn];     // 每个油站距离起点油价 
double dist[maxn];		// 每个油站距离起点的距离 

double D1,C,D2,P;
int N;

double maxDistance = 0;// 所能行驶的最远距离 

double total = 0,remain = 0; // 总花费、剩余 油/升 

int main(void) {
	scanf("%lf%lf%lf%lf%d",&D1,&C,&D2,&P,&N);
	maxDistance = C * D2;
	bool flag = true;
	for(int i = 1; i <= N; i ++) {
		scanf("%lf%lf",&dist[i],&price[i]);
		// 每一段都应该  <= 所能行驶的最大距离 
		if(dist[i] - dist[i - 1] > maxDistance) flag = false;
	}	
	if(!flag) {
		printf("No Solution\n");
		return 0;
	}
	// 加入起始地和目的地 
	dist[0] = 0,price[0] = P;
	dist[N + 1] = D1,price[N + 1] = 0;
	int i,j ;
	for(i = 0; i <= N; i = j) {
		for(j = i + 1; j <= N + 1; j ++) {
			// 当前油量所能到达的最远距离 
			if(dist[j] - dist[i] > maxDistance) {
				j --;
				break;
			}
			// 找到了合适的价格 
			if(price[j] <= price[i]) {
				break;
			}
		}
		// 详情看图 
		if(price[j] <= price[i]) {
			total += ((dist[j] - dist[i]) / D2 - remain) * price[i];
			remain = 0;
		} else {
			total += (C - remain) * price[i];
			remain = C - (dist[j] - dist[i]) / D2;
		}
	}
	
	printf("%.2lf\n",total);
	return 0;
	
}

后记:

这题想着想着就不知道想到哪了，哈哈
反悔贪心还是第一次见，孤陋寡闻了，还需要找几道题练习一下。
不过感觉这种思维着实不错，就是忒麻烦，嘻嘻。
加油！奥利给！

参考链接:

反悔贪心

[每日一题]:P1016 旅行家的预算 -- 反悔贪心

标签：src   log   快速   贪心   string   flag   ref   algo   小根堆   

原文地址：https://www.cnblogs.com/prjruckyone/p/12770903.html