标签:数据存储 let 台阶 out 函数 base 总结 最新 c++
栈和队列
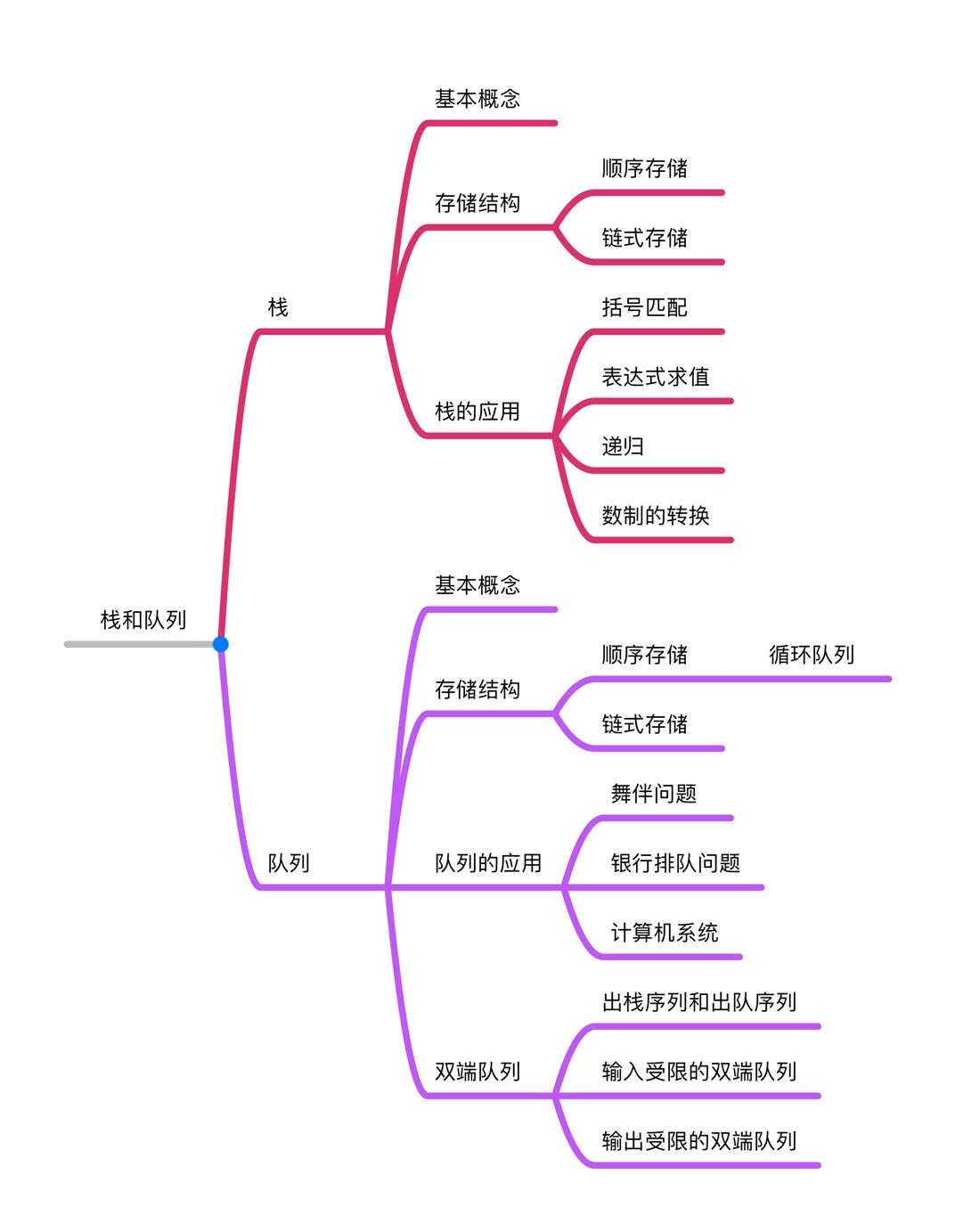
栈和队列的定义和特点
栈(stack):仅在表尾进行插入或删除操作 表尾(栈顶) 表头(栈底) 后进先出
队列(queue):只允许在表的一端进行插入,另一端删除元素 插入端(队尾rear) 删除端(队头front)先进先出
#案例引入
数制的转换:非负十进制整数->等值八进制数 产生:从低位到高位 输出:从高位到低位>>栈
算法思想:
1)初始化一个空栈
2)当十进制数N非零时,循环执行以下操作
把N与8求余得到的八进制数压入栈S
N更新为N与8的商
3)当栈S非空时,循环执行以下操作
弹出栈顶元素e
输出e
括号匹配的检验:“期待的急迫程度” 右括号(置于栈顶期待消解/不合法) 左括号(新的更急迫压入栈中)>>栈
算法思想:
1)初始化一个空栈S,设置flag=1,顺序读入括号
2)若是右括号,则与栈顶元素进行匹配 匹配:则弹出栈顶元素并进行下一个匹配 不匹配:则该序列不合法,flag=0
3)若是左括号,则压入栈中
4)若全部元素遍历完毕,栈中非空则序列不合法
表达式求值:“算符优先法”前缀表达式+AB 中缀表达式A+B 后缀表达式AB+ 将中缀表达式转化为前缀表达式或后缀表达式
中缀转后缀算法思想:
数字直接加入后缀表达式
运算符时:
a.若为‘(’,入栈
b.若为‘)’,则依次把栈中的运算符加入后缀表达式,直到出现‘(’,并从栈中删除‘(’
c.若为‘+’‘-’‘*’‘/’
栈空,入栈
栈顶元素为‘(’,入栈
高于栈顶元素优先级,入栈
否则,依次弹出栈顶运算符,直到一个优先级比它低的运算符或‘(’为止
d.遍历完成,若栈非空,依次弹出所有元素
舞伴问题:先入队的男士女士先配对>>队列
算法思想:
1)初始化Mdancers队列和Fdancers队列
2)反复循环,依次将跳舞者根据其性别插入Mdancers队列或Fdancers队列
3)当Mdancers队列和Fdancers队列均为非空时,反复循环,依次输出男女舞伴的姓名
4)如果Mdancers队列为空而Fdancers队列非空,则输出Fdancers队列的队头女士的姓名
5)如果Fdancers队列为空而Mdancers队列非空,则输出Mdancers队列的队头男士的姓名
栈的表示和操作的实现
栈的类型定义:

顺序栈的表示和实现:
图3.3.2 顺序存储结构实现栈(需另设base指明栈底元素位置) 空栈表示(top==base)
初始化:1.动态分配MAXSIZE大小的数组,base->基地址 2.top初始化为base(栈为空) 3.stacsize==MAXSIZE
入栈:在栈顶插入一个新元素 1.栈满->退出 2.新元素压入栈顶,top++
出栈: 将栈顶元素删除 1.空栈->退出 2.top--,元素赋给e
取栈顶元素:栈非空,返回当前栈顶元素的值(栈顶指针不变)

链栈的表示和实现
图3.3.3 链式存储结构实现栈(通常用单链,表头作栈顶,不需要附加头结点)

初始化:直接将栈顶指针置空(NULL)
入栈:图3.6 无需判断栈满,动态分配空间

出栈:1.空栈->退出 2.赋值 3.保存栈顶空间 4.修改栈顶指针 5.释放原栈顶元素空间
取栈顶元素:栈非空->返回元素值
栈与递归
采用递归算法解决的问题:
定义是递归的:阶乘函数 “分治法”条件:1.新问题和原问题解法相似 2.递归可简化问题 3.有明确出口(递归边界)
数据结构是递归的:遍历链表
问题解法是递归的:n阶汉诺塔
递归过程与递归工作栈:“后调用先返回”递归工作栈:递归函数运行期间使用的数据存储区 活动记录:当前执行层的工作记录必是递归工作栈栈顶的工作记录
递归算法的效率分析:
时间复杂度:迭代法
空间复杂度:分析工作栈的大小 S(n)=O(f(n))
利用栈将递归转化为非递归的方法
队列的表示和操作的实现
*删除是在表的头部(即队头)进行
循环队列——队列的顺序表示和实现

解决“假溢出”->利用Q.rear的“模”运算
判断队满/队空:1)少用一个元素空间 2)设定标志位区别队列满/空
初始化:分配MAXQSIZE数组空间,base指向首地址 2.头尾指针置零
求队列长度:非循环:尾指针-头指针 循环:(尾指针-头指针+MAXQSIZE)/MAXQSIZE
入队:在队尾插入一个新元素 1.判断队满 2.新元素插入队尾 3.Q.rear++
出队:将队头元素删除 1.判断空队 2.保存队头元素 3.Q.front++
取队头元素:队列非空,返回Q.front->data
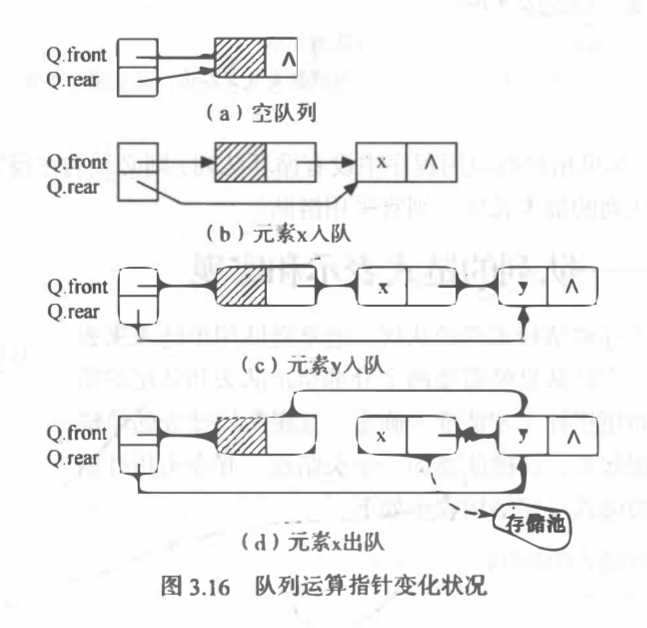
链队————队列的链式表示和实现 p73
初始化:是构造一个只有一个头结点的空队 1.生成新结点作为头结点,队头和队尾指针指向此结点 2.头结点置空
入队:1.为新元素分配结点空间 2.新结点数据域置为e 3.新结点插到队尾 4.Q.rear=p;
出队:1.判断队空 2.(临时)保存队头元素空间 3.Q.front->next=p->next; 4.判断出队元素是否为最后一个元素,若是,则将队尾指针重新赋值, 指向头结点。 5.释放原队头元素空间
取队头元素:队列非空,返回当前队头元素的值
双端队列
连续输入/输出
输入序列:1,2,3,...,n 栈输出:n,...,3,2,1(输入序列的逆序) 队列输出:1,2,3,...,n(为输入序列的顺序)
非连续输入/输出
输入序列:1,2,3 栈输出:3,1,2(不合法)
*栈输出合法规律:出栈序列中每一个元素后面所有比它小的元素组成一个递减序列
合法出栈序列的个数
进栈序列:1,2,3,...,k,...,n
出栈序列:...,1/...,2/...,k/...,n-1/...,n
eg:...,k(k为最后一个出栈元素)出栈序列:1~k-1/k+1~n/k 所有以k为最后一个输出元素的合法序列的个数=f(k-1)*f(n-k)//f表示出栈序列个数的函数,f(k-1)表示k-1个数的合法出栈序列,f(n-k)表示n-k个元素的合法出栈序列的个数
>>f(n)=f(0)*f(n-1)+f(1)*f(n-2)+...+f(n-2)*f(1)+f(n-1)*f(0) //f(0)=f(1)=1
>>f(n)=C(2n,n)/(n+1)//C:组合数,2n在下标,n在上标
双端队列
允许两端都可以进行入队及出队操作的队列,无论哪一端都是先出的元素在前,后出的元素在后
输入序列:1,2,3,4
1)输出受限的双端队列
屏蔽一端的输入操作后相当于栈,所以所有对栈合法的输出序列都对该队列合法
在栈中非法输出序列的个数=4!-C(8,4)/(4+1)=10
4231和4132非法
2)输入受限的双端队列
屏蔽一端的删除操作后相当于栈,所以所有对栈合法的输出序列都对该队列合法
在栈中非法输出序列的个数=4!-C(8,4)/(4+1)=10
4231和4213非法
————————————————————————————
//共享栈:将两个栈顶设置在共享空间的两端,栈顶向空间中间延伸
//判空条件:0号栈top==-1 1号栈top==MAXSIZE
//栈满条件:top1-top0==1
//优点:存取时间复杂度仍为O(1),但空间利用更加有效
4.13提问
void Delete(List &L) {//函数作用:删除链表的首元结点,并将其后移 if (L.head->next == NULL) {//判断空表,若为空则输出"Empty list"后退出 cout << "Empty list" << endl; return; } }
4.13讨论
#define MaxSize 100 ElementType S[MaxSize]; int top; void Push(ElementType *S, int top, ElementType item) { if (top==MaxSize-1) {//此处的应该是top==MAXSIZE //原因是top的值始终为“当前最新元素下标值++” //而C++数组又是从0号下标开始的,所以当满栈时top==MAXSIZE printf(“堆栈满”); return; } else { S[++top] = item; //此处应该是S[top] = item; top++;/S[top++] = item; //原因和上面差不多,top的值始终为“当前最新元素下标值++” //而C++数组又是从0号下标开始的,我们需要先给下标为top的位置赋值,再top++ return; } }
4.14讨论2 爬楼梯
#include<iostream> using namespace std; //假设有n级台阶要走 //若最后走1级,则之前走了n-1个台阶,走法有f(n-1)种 //若最后走2级,则之前走了n-2个台阶,走法有f(n-2)种 //所以最终的走法 等于 最后三次走法之和 //当有10级台阶时,f(10) = f(9) + f(8) +f(7) //f(9) = f(8) + f(7) + f(6), f(8) = f(7) + f(6) + f(5) ...... //通过递归可以得出最后结果 int climbStairs(int n) { if(n<=0) return 0;//当n不合法时 else if(n==1) return 1;//当0<n<=2时,走法为即为n else if(n==2) return 2; else if(n==3) return 4;//此处也可以放入递归计算
else return climbStairs(n-1)+climbStairs(n-2)+climbStairs(n-3);//f(n)=f(n-1)+f(n-2)+f(n-3) } //当n=10时,走法有274种
标签:数据存储 let 台阶 out 函数 base 总结 最新 c++
原文地址:https://www.cnblogs.com/cmlearning/p/12775967.html