深度优先搜索

标签：oid   表示   cout   大小   end   for   测试数据   inf   回溯   

深度优先搜索的思想是思想是从一个顶点V0开始，沿着一条路一直走到底，如果发现不能到达目标解，那就返回到上一个节点，然后从另一条路开始走到底。

即：往深处走。

例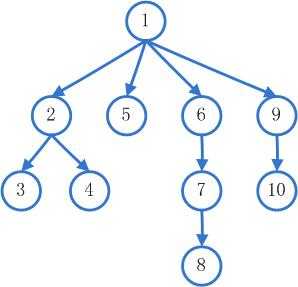：从这个图中，深度优先搜索的顺序就是1->2->3->2->4->2->1->5->1->6->7->8->7->6->1->9->10

代码模板：void dfs(int x,int y,int step)
{
        判断边界
        {
            相应操作
        }
        尝试每一种可能
        {
               满足check条件
               标记
               继续下一步dfs(step+1)
               恢复初始状态（回溯的时候要用到）
        }
}  
使用深度优先搜索其实可以解决大部分考试试题，虽然因为该算法时间复杂度极大，大多数情况只能得一点分。。。

例题： 

马在中国象棋以日字形规则移动。

请编写一段程序，给定n×m大小的棋盘，以及马的初始位置(x，y)，要求不能重复经过棋盘上的同一个点，计算马可以有多少途径遍历棋盘上的所有点。

【输入】

第一行为整数T(T < 10)，表示测试数据组数。

每一组测试数据包含一行，为四个整数，分别为棋盘的大小以及初始位置坐标n,m,x,y。(0≤x≤n-1,0≤y≤m-1, m < 10, n < 10)。

【输出】

void dfs(int x,int y,int step)
{    if(step==n*m)  
 {
        cnt++;
        return;    }   
 for(int i=0;i<8;i++)   
 {
       int nx=x+dir[i][0];
        int ny=y+dir[i][1];
        if(nx>=0&&ny>=0&&nx<n&&ny<m&&vis[nx][ny]==0)
        {
            vis[nx][ny]=1;
            dfs(nx,ny,step+1);
            vis[nx][ny]=0;        }    }}
int main()
{    int t;
    cin>>t;
    while(t--)
    {
       cnt=0;
        memset(vis,0,sizeof(vis));
         cin>>n>>m;
         cin>>x0>>y0;
         vis[x0][y0]=1;
        dfs(x0,y0,1);
        cout<<cnt<<endl;
    }   
    return 0;}

每组测试数据包含一行，为一个整数，表示马能遍历棋盘的途径总数，0为无法遍历一次。

深度优先搜索

标签：oid   表示   cout   大小   end   for   测试数据   inf   回溯   

原文地址：https://www.cnblogs.com/lixiangtu/p/12775935.html