三维坐标旋转矩阵

标签：协议   detail   尺寸   向量   inf   一个   角度   旋转矩阵   二维   

1.三维坐标旋转矩阵的推导过程

任何维的旋转可以表述为向量与合适尺寸的方阵的乘积。最终一个旋转等价于在另一个不同坐标系下对点位置的重新表述。 坐标系旋转角度θ则等同于将目标点围绕坐标原点反方向旋转同样的角度θ。

若以坐标系的三个坐标轴X、Y、Z分别作为旋转轴，则点实际上只在垂直坐标轴的平面上作二维旋转。

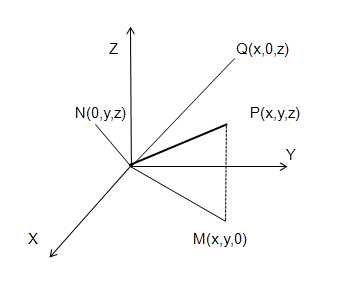
假设三维坐标系(右手坐标系,拇指即指向X轴的正方向。伸出食指和中指，如右图所示，食指指向Y轴的正方向，中指所指示的方向即是Z轴的正方向。要确定轴的正旋转方向，用右手的大拇指指向轴的正方向，弯曲手指。那么手指所指示的方向即是轴的正旋转方向)中的某一向量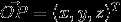，其在直角坐标系中的图如图1所示。其中点P在XY平面、XZ平面、YZ平面的投影分别为点M、点Q、点N。

 一、绕Z轴逆时针旋转θ角 

绕Z轴旋转，相当于在XY平面的投影OM绕原点逆时针旋转，如下图所示，OM旋转θ角到OM’。      

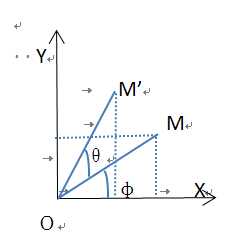
 设旋转前的坐标为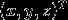，旋转后的坐标为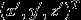，则点M的坐标为（x，y），点M’的坐标为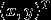。由此可得：

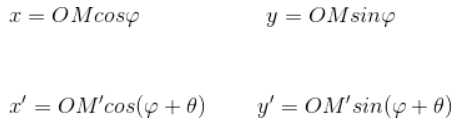
对于和进行三角展开可得：

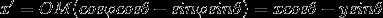
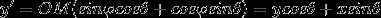
 且有;可得绕Z轴旋转角的旋转矩阵为：    

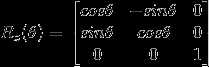
 由此可得： 

二. 绕X轴逆时针旋转θ角

 三. 绕Y轴逆时针旋转θ角

以上旋转矩阵都是在右手坐标系下计算的。三维旋转矩阵就可由以上三个矩阵相乘得到。
这里的旋转矩阵是需要左乘的，而且以逆时针为正。R是一个旋转矩阵，X是一个三维列向量[x,y,z]’。
RX就是把X旋转。

 ————————————————

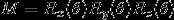
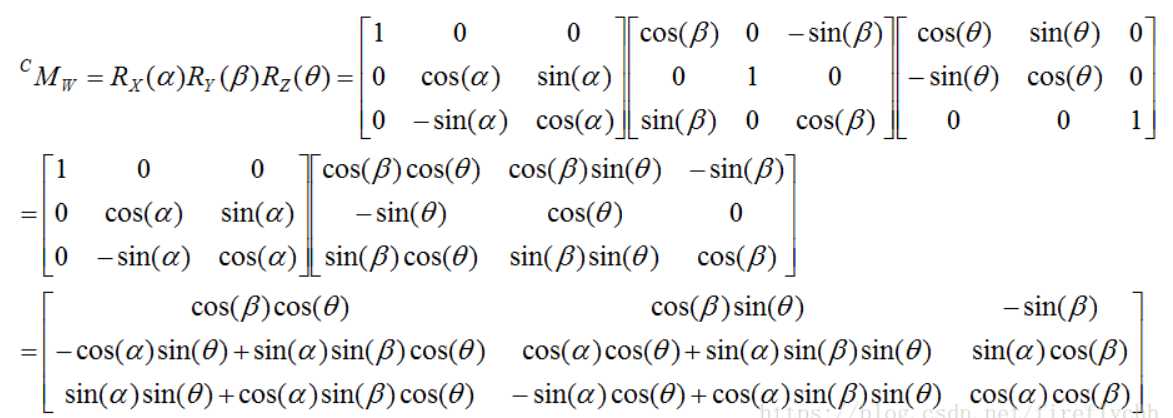
版权声明：本文为CSDN博主「坚持奋斗的李洛克」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/lz20120808/java/article/details/50809397

三维坐标旋转矩阵

标签：协议   detail   尺寸   向量   inf   一个   角度   旋转矩阵   二维   

原文地址：https://www.cnblogs.com/mryu119/p/12776369.html