标签:线性 法线 turn 技术 距离 proc 关于 sub als
1、已知平面上一点p、法线N 求平面方程
法向量N: N(a,b,c) 点P: p(x0, y0, z0) 平面方程: a(x-x0)+b(y-y0)+c(z-z0)=0;
A = a
B = b
C = c
D = -1*(a*x0+b*y0+c*z0)
Ax+By+Cz+D=0;
综上所述方程Ax+By+Cz+D=0各参数的意义
(A,B,C)法向量的分量,D,原点到平面的距离
2、已知平面三点P1(x1, y1, z1), P2(x2, y2, z2), P3(x3, y3, z3), 求平面方程
a、线性解法
求过三zhidao点:M?(x?,y?,z?);M?(x?,y?,z?);M?(x?,y?,z?)的平面的方法: 设过M?的平面方程为 A(x-x?)+B(y-y?)+C(z-z?)=0.................① M?,M?都在此平面上,因此它们的坐标都满足方程①;将它们的坐标依专次代入得: A(x?-x?)+B(y?-y?)+C(z?-z?)=0.............② A(x?-x?)+B(y?-y?)+C(z?-z?)=0..............③ ①②③是关于A、B、C的线性方程组,此方程组有非零解的充要条件是关于A、B、C的系数 行列属式?=0;即:
求过三zhidao点:M?(x?,y?,z?);M?(x?,y?,z?);M?(x?,y?,z?)的平面的方法:
设过M?的平面方程为 A(x-x?)+B(y-y?)+C(z-z?)=0.................①
M?,M?都在此平面上,因此它们的坐标都满足方程①;将它们的坐标依专次代入得:
A(x?-x?)+B(y?-y?)+C(z?-z?)=0.............②
A(x?-x?)+B(y?-y?)+C(z?-z?)=0..............③
①②③是关于A、B、C的线性方程组,此方程组有非零解的充要条件是关于A、B、C的系数
行列属式?=0;即:
打开此行列式,就可得到所求平面的方程。
D=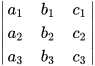 =
=
b、克莱姆法则
平面方程:
Ax+By+Cz+D=0 (参数,A,B,C,D是描述平面空间特征的常数)

//根据3个点,计算空间平面的方程 //Ax+By+Cz+D=0 //输入参数:in_points---空间中3个点的坐标,大小为3;输入点>3时,只取前3个点 //输出参数A,B,C,D //返回值:0---计算成功;-1----计算失败 int GetPlaneEquation(vector<PointT> &in_points, float &A, float &B, float &C, float &D) { if( in_points.size() <3 ) { cerr<<"GetPanelEquation(...)函数中输入点的数量小于3."<<endl; return false; } A = in_points[0].y*(in_points[1].z-in_points[2].z) + in_points[1].y*(in_points[2].z-in_points[0].z) + in_points[2].y*(in_points[0].z-in_points[1].z); B = in_points[0].z*(in_points[1].x-in_points[2].x) + in_points[1].z*(in_points[2].x-in_points[0].x) + in_points[2].z*(in_points[0].x-in_points[1].x); C = in_points[0].x*(in_points[1].y-in_points[2].y) + in_points[1].x*(in_points[2].y-in_points[0].y) + in_points[2].x*(in_points[0].y-in_points[1].y); D = -in_points[0].x*(in_points[1].y*in_points[2].z - in_points[2].y*in_points[1].z) - in_points[1].x*(in_points[2].y*in_points[0].z - in_points[0].y*in_points[2].z) - in_points[2].x*(in_points[0].y*in_points[1].z - in_points[1].y*in_points[0].z); return 0; }
c、其他
A = (y2 - y1)*(z3 - z1) - (z2 -z1)*(y3 - y1); B = (x3 - x1)*(z2 - z1) - (x2 - x1)*(z3 - z1); C = (x2 - x1)*(y3 - y1) - (x3 - x1)*(y2 - y1); 即得过P1,P2,P3的平面方程 方程也可写为 Ax + By + Cz + D = 0 (一般式) 其中D = -(A * x1 + B * y1 + C * z1)
d、也可以三个点 构造两个向量 进行叉乘 得到平面法线,再利用点法式求得。
标签:线性 法线 turn 技术 距离 proc 关于 sub als
原文地址:https://www.cnblogs.com/lovebay/p/12777556.html