多项式运算

时间：2020-04-26 19:12:31 阅读：87 评论：0 收藏：0 [点我收藏+]

标签：情况 style typedef 拓展 tps 问题 radius family height

编译环境说明，以下代码能够在 codeblocks 16.01 自带编译器版本中， C语言 项目中正确运行，没有警告，没有错误，如果，更换为其它环境，例如 DEV 请自行修改编译器不同造成的差异。

前言

一元多项式计算器没有用链表写这个多项式之前，哇，觉得这个好难啊！！！链表是人干出来的事情？？写完了才发现，“真香警告”。（︶^︶）我才不会承认的。

基本变量

变量名	描述
c	系数
n	幂值

程序模块

函数名	描述
input()	返回一个多项式升序链表
insert(int c, int n, LIST head)	改良的插入方法，升序插入和幂值相同控制
add(LIST A, LIST B)	两个多项式相加
sub(LIST A, LIST B)	多项式相减 A - B
mul(LIST A, LIST B)	多项式相乘 A * B
output(LIST head)	按照一定形式输出多项式
reversed(LIST head)	链表反转（降幂）
uptate(LIST head)	更新链表的信息（删除系数为0的结点）
show(LIST head)	对输出方法（降幂，升幂，return）封装
init()	对运算函数（add，sub，mul）封装

构建输入函数

不管会不会，输入是必须的，先把数据读入再说。既然选用了链表存储，用链表来实现，那么我们肯定要考虑到链表的两种形式：带头结点的链表和不带头结点的链表，这两种有什么区别呢？

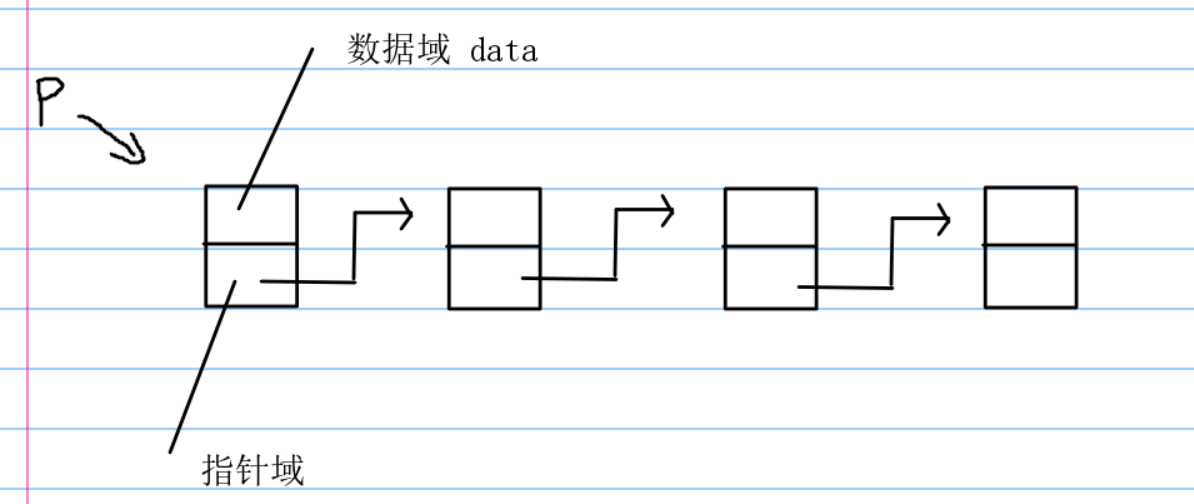
同时我们还需要了解下面三个概念：（不想看直接跳过，我已经整理成图片的形式了）

名称	解释说明
首元节点	就是指链表中存储第一个数据元素a1的结点。
头结点	它是在首元结点之前附设的一个节点，其指针域指向首元结点。头结点的数据域可以不存储任何信息，也可以存储与数据元素类型的其他附加信息，例如，当数据元素为整数型时，头结点的数据域中可存放该线性表的长度。如上表中的数据域和指针域（在链表和线性中一个结点包含两个域：一个是数据域，另外一个是指针域，指针域它本有自己的存储地址，同时又指向下一个节点的数据域，这就形成了一个逻辑关系）就是一个头结点。
头指针	它是指向链表中的第一个结点的指针。若链表设有头结点，则头指针所指结点为线性表的头结点；若链表不设头结点，则头指针所指结点为该线性表的首元结点。

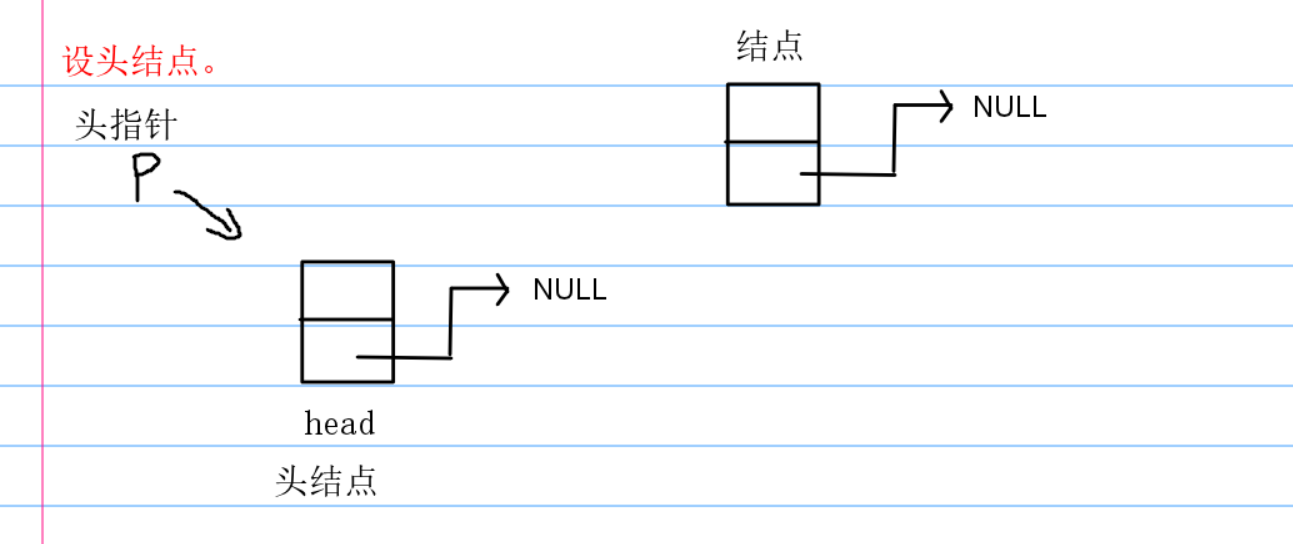
下面是图片辅助理解：

带头结点

不带头结点

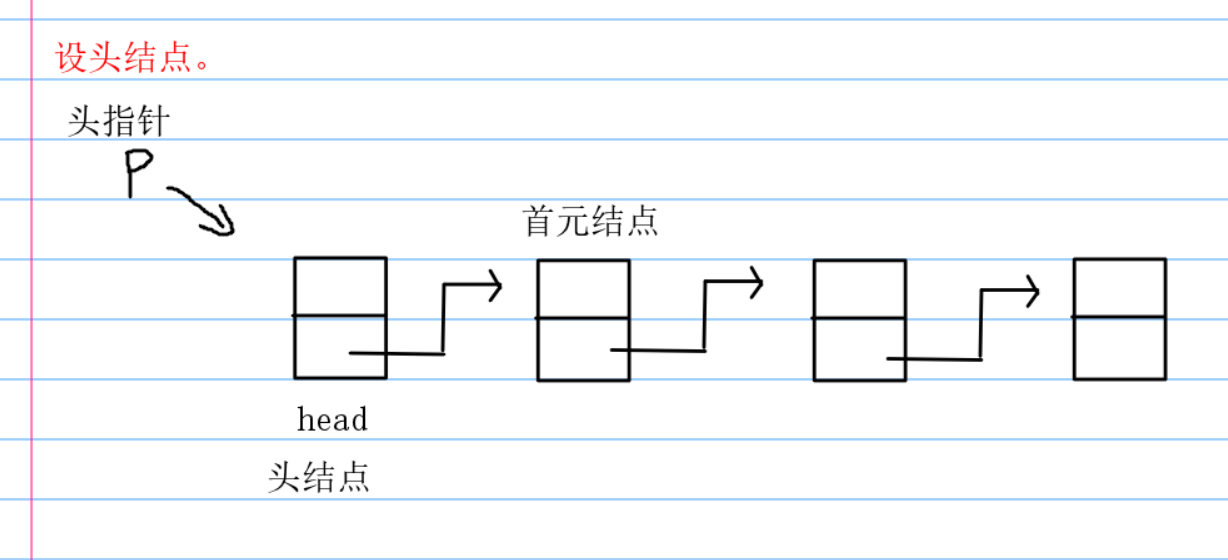
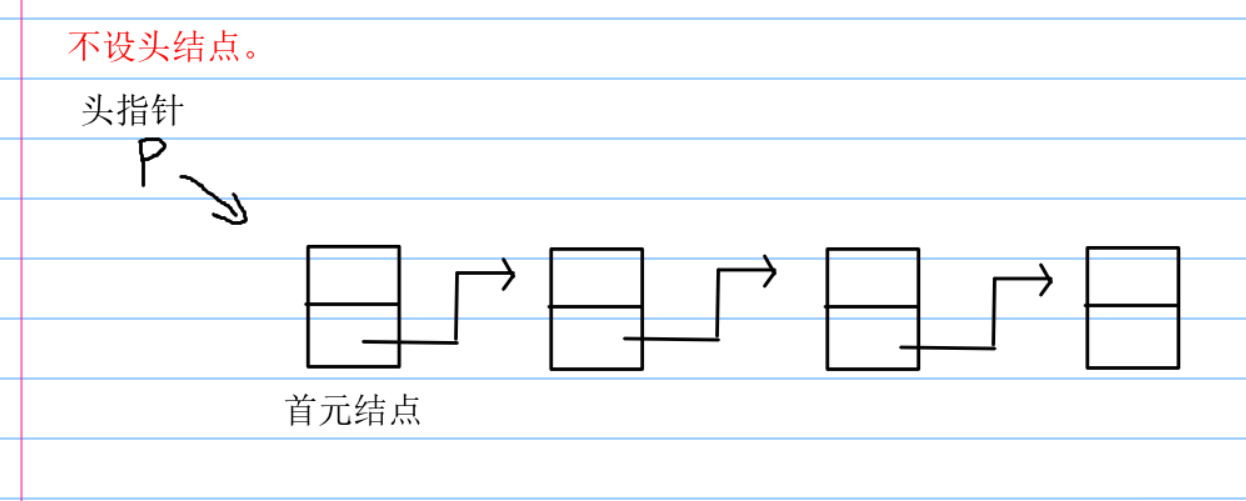
那么看到这个地方，我的选择是带头结点。原因是一般的链表都带头结点，另外就是，带头结点，插入，查找，删除都比较方便。

输入函数的写法

首先看到这个地方，我们需要有一个头指针，暂时标记为head，这个指针这这个地方不存储人任何元素（实际操作这个头结点的数据域可以存储元素，比如链表长度）。

其次，我们应该考虑输入的多项式的格式问题：

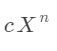
特征提取得到两个关键的元素，系数和指数。这样考虑的原因是因为，X是固定不变的，没有逻辑上的意义，所以不考虑，那么我们得到这些，就可以每次申请一块地址空间，来存放多项式中的某一项，链表的一般方法是插入。我们假定有这样一个方法，那么我们如何存储链呢？

第一种就是尾插法，节点一直插入到链表的尾部：

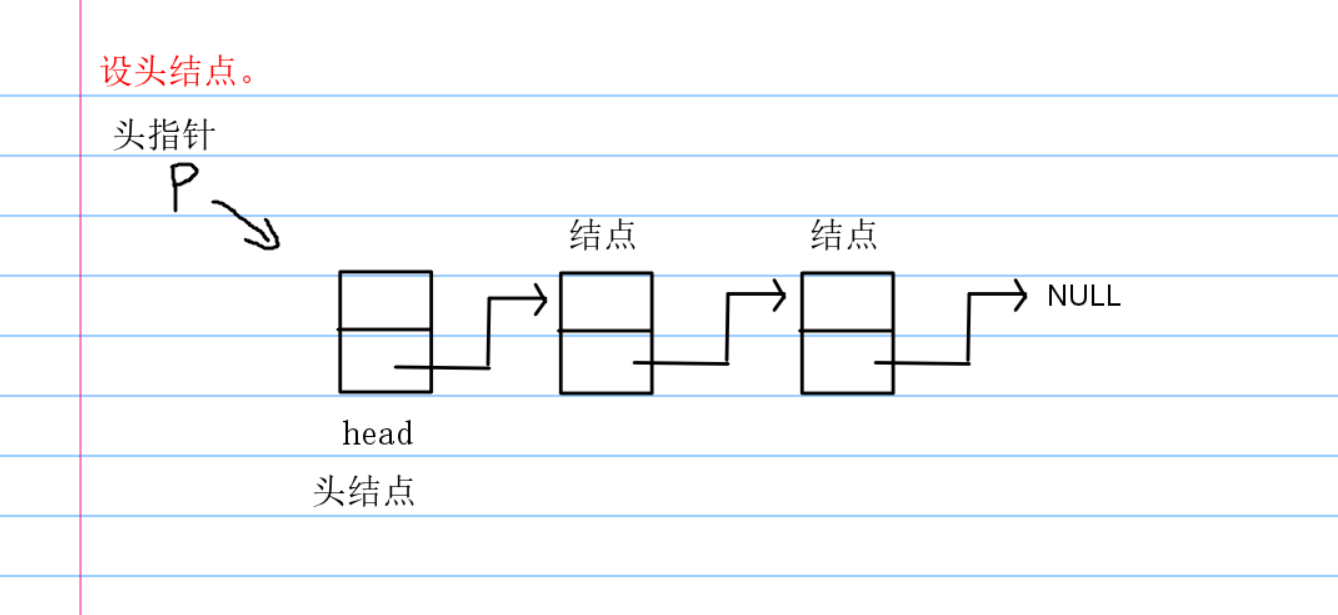
这种方式存储我们的链表当然可以。

我们假定我们已经写了 insert 函数

LIST input()
{
    printf("输入系数和指数，以0 0结束\n");
    //输入系数和指数
    LIST head = (LIST)malloc(sizeof(struct node));
    head->NEXT = NULL;
    int n, c;
    while(scanf("%d%d", &c, &n), n || c)
        insert(c, n, head);
    return head;
}

可以看到返回的是链表类型。

那么我们可以直接调用。

printf("请先输入两个多项式\n");
LIST A = input();
LIST B = input();

构建插入函数`insert`

刚刚呢我们假设了有一个这样的 insert 函数，把所有的结点都插入在链表的尾部，那么会造成什么样的情况呢？

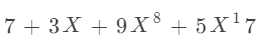
如果是按照这样升幂输入的数据当然没问题，但也有可能输入的数据是这样的：

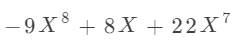
类似于我们这样的无序输入，那么我们下一步，肯定需要进行排序的操作，把这个变成升幂或者降幂的形式。那既然这样，为什么我们不直接就让这个链表有序插入呢？我们知道，链表的优势就是易拓展，也就是可以在中间直接插入某元素。

这就是关键的地方！！！插入的时候就维持有序状态。

那么是不是还有别的情况？

比如说这两个值相同，换句话说，这两个幂值相同，根据运算的原理，系数肯定是要相加的。

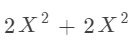
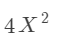
这两个在实际计算过程中是等价的。

所以，我们直接在插入的时候就考虑这两种情况！！

演示：

找不到的情况：

代码如下：

void insert(int c, int n, LIST head)
{
    //头结点性质
    LIST tmp = (LIST)malloc(sizeof(struct node));
    tmp->n = n, tmp->c = c, tmp->NEXT = NULL;
    LIST P = head;
    while(P->NEXT)
    {
        //相等
        if(P->NEXT->n == tmp->n)
        {
            P->NEXT->c += tmp->c;
            return;
        }
        if(P->NEXT->n > tmp->n)
            break;
        P = P->NEXT;
    }
    //找到最后还没有找到
    if(!P->NEXT)
    {
        P->NEXT = tmp;
        return;
    }
    tmp->NEXT = P->NEXT;
    P->NEXT = tmp;
}

关于加法

有了上面的铺垫是不是问题就非常简单啦！！！

insert 实现了升序和处理相同值的情况，那么加法怎么加呢？

第一种就是A链为母链，B链的所有结点都添加到（insert）A链中。

第二种就是B链为母链，A链的所有结点都添加到（insert）B链中。

第三种就是新增一条链，A链和B链的所有结点都添加到（insert）新链中。

代码如下（使用的第三种方法）：

void add(LIST A, LIST B)
{
    LIST head = (LIST)malloc(sizeof(struct node));
    head->NEXT = NULL;
    LIST P = A->NEXT;
    while(P)
        insert(P->c, P->n, head), P = P->NEXT;
    P = B->NEXT;
    while(P)
        insert(P->c, P->n, head), P = P->NEXT;
    uptate(head);//暂时忽略
    show(head);//暂时忽略
}

P从A的首元节点到最末尾，然后从B的首元节点到末尾，也就是把A链和B链的所有结点都添加到（insert）新链中。

关于减法

有了加法，减法还会远吗？

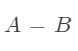
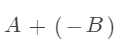
这两个形式在值上面是等价的。

那么我们直接在加法的基础上面变形。

第一种就是A链为母链，B链的所有结点的系数的相反数都添加到（insert）A链中。

第二种就是B链为母链，A链的所有结点的系数的相反数都添加到（insert）B链中。

第三种就是新增一条链，A链和B链的所有结点的系数的相反数都添加到（insert）新链中。

P从A的首元节点到最末尾，然后从B的首元节点到末尾，也就是把A链和B链的所有结点的系数的相反数添加到（insert）新链中。

代码如下（使用的第三种方法）：

void sub(LIST A, LIST B)
{
    LIST head = (LIST)malloc(sizeof(struct node));
    head->NEXT = NULL;
    LIST P = A->NEXT;
    while(P)
        insert(P->c, P->n, head), P = P->NEXT;
    P = B->NEXT;
    while(P)
        insert(-P->c, P->n, head), P = P->NEXT;
    uptate(head);//暂时忽略
    show(head);//暂时忽略
}

关于乘法

有了之前加法和乘法的思路，乘法就不用我说了。

遍历A链的所有结点，遍历B链的所有结点，也就是双重循环，AXB的所有结点添加（insert）到新链中。

因为我们规定的 insert 就是有序，不重复幂值。

所以直接丢进去就行，不用考虑。

void mul(LIST A, LIST B)
{
    LIST head = (LIST)malloc(sizeof(struct node));
    head->NEXT = NULL;
    LIST i = A->NEXT;
    //if A NULL
    LIST j = B->NEXT;
    if(!i)
    {
        while(j)
        {
            insert(j->c, j->n, head);
            j = j->NEXT;
        }
        uptate(head);
        show(head);
        return;
    }
    //if B NULL
    if(!j)
    {
        while(i)
        {
            insert(i->c, i->n, head);
            i = i->NEXT;
        }
        uptate(head);
        show(head);
        return;
    }
    while(i){
        j = B->NEXT;
        while(j)
        {
            insert(i->c * j->c, i->n + j->n, head);
            j = j->NEXT;
        }
        i = i->NEXT;
    }
    uptate(head);
    show(head);
}

非法值处理

什么样的值是特殊的？非法的？肯定是不符合我们规定的形式的。

那么我们可以得到，系数为0，其实这一项就是没有了，所以，剔除。

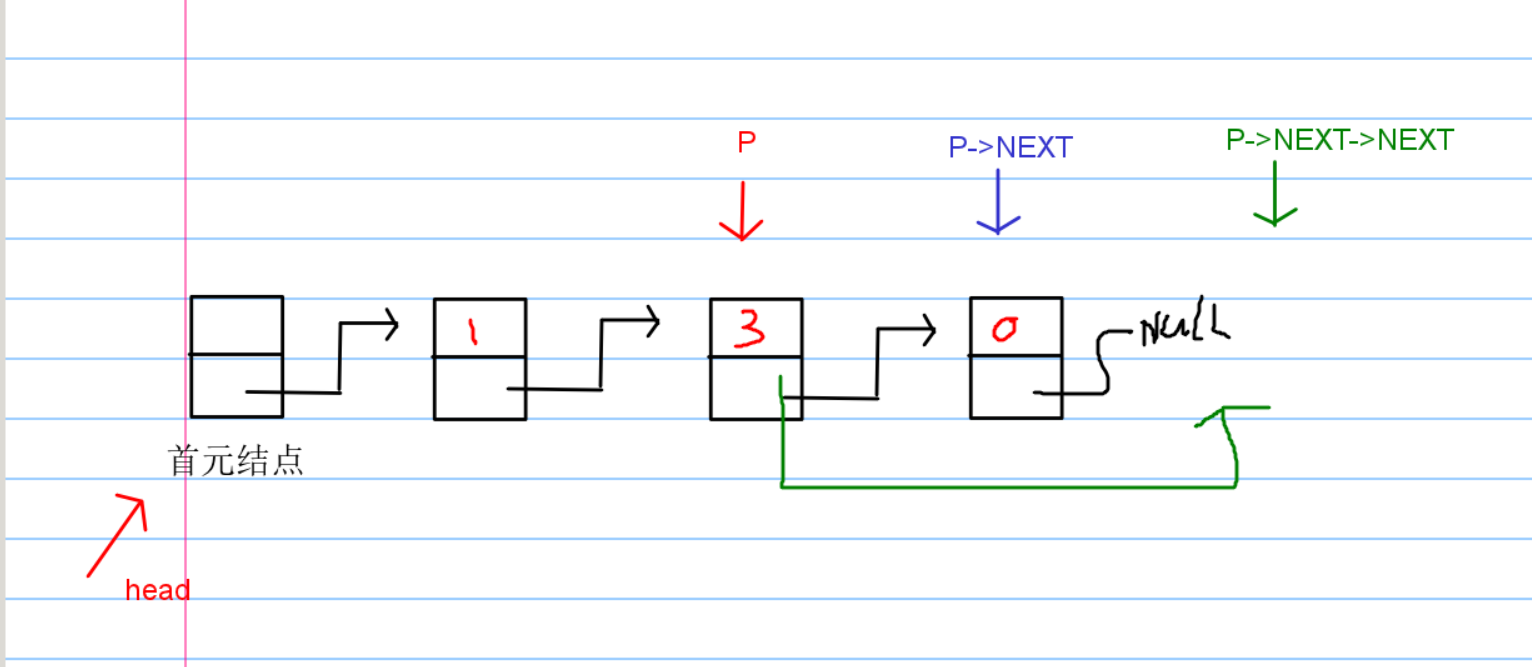
这里就体现了 头结点 的方便之处，本质上来说，这段代码属于，链表的删除。

基本思想就是：

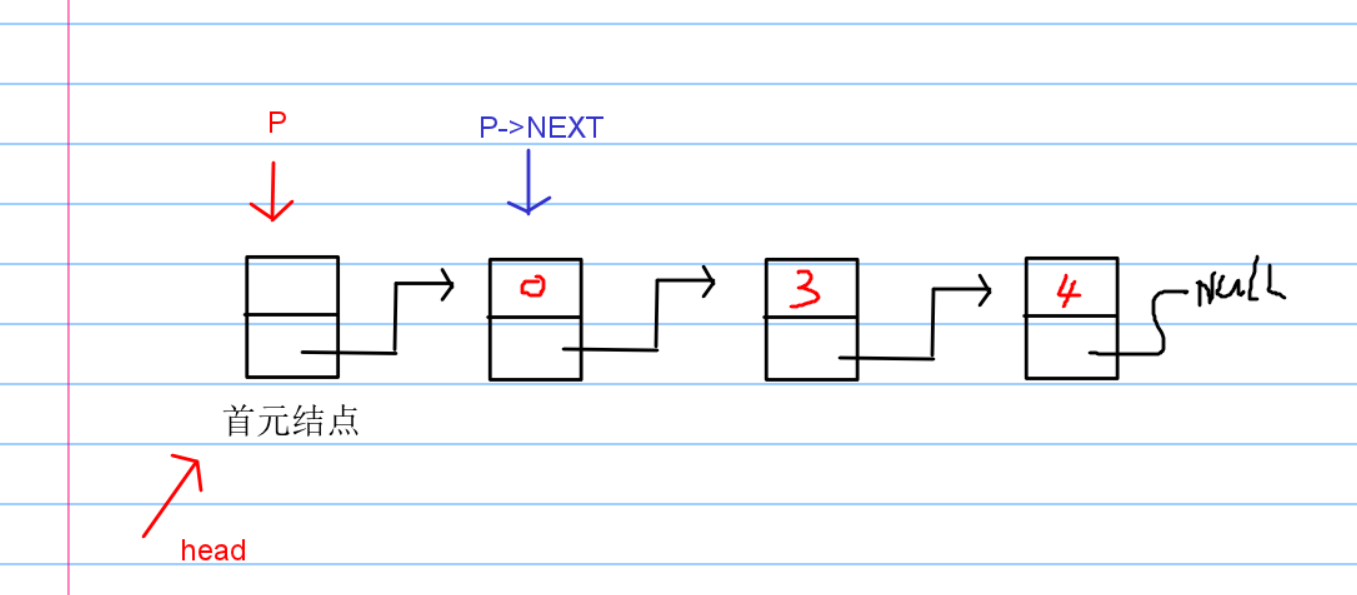
怎么剔除呢？

P->NEXT = P->NEXT->NEXT;

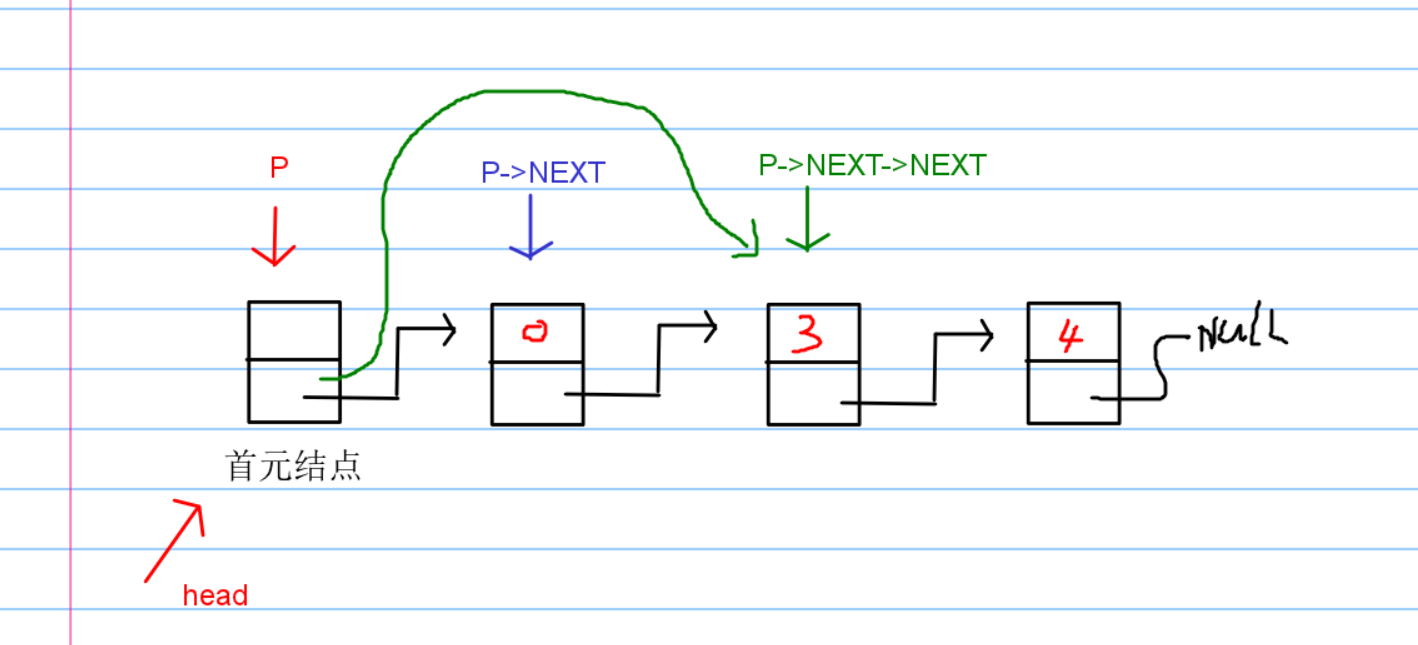
这样可能会说，有bug，真的有么？

就算我是最后一个结点，也没有问题。

void uptate(LIST head)
{
    LIST P = head;
    while(P->NEXT)
    {
        if(P->NEXT->c == 0){
            P->NEXT = P->NEXT->NEXT;
            continue;
        }
        P = P->NEXT;
    }
}

关于输出

输出就是考虑特殊值，比如说正好，负号，首次输出的符号。

考虑到这些，应该就没有问题了。

首个值，那就让指针动一下，然后 P=P->NEXT 就ok了；

代码如下：

void output(LIST head)
{
    LIST P = head->NEXT;
    if(!p) return;
    //输出第一个
    if(P->c < 0)
        printf("-");
    if(P->n == 0)
        printf("%d", abs(P->c));
    else
        printf("%dx^%d", abs(P->c), P->n);
    P = P->NEXT;
    //继续输出
    while(P)
    {
        if(P->n == 0)
            printf("%c%d", P->c > 0 ? ‘+‘ : ‘-‘,abs(P->c));
        else
            printf("%c%dx^%d", P->c > 0 ? ‘+‘ : ‘-‘, abs(P->c), P->n);
        P = P->NEXT;
    }
    printf("\n");
}

两次封装

说白了，就是别人看着舒服。( ╯□╰ )

主要运用 switch 语句。

第一层封装是在main函数。主要以下功能：

名称	编号	功能
add(A, B)	1	A + B
sub(A, B)	2	A - B
sub(B, A)	3	B - A
mul(A, B)	4	A * B
return	5	返回上一级（结束）

第二层封装主要是三种运算关系调用：

名称	编号	功能
升幂	1	升幂展示多项式
降幂	2	降幂展示多项式
all	3	升序降幂
return	4	返回上一级

执行结果

测试数据

A,B都由常数构成

A = 5; B = 7

A, B常数和多项式

A = 6; B = 7X^2 + 5 X^ 3 + 3

A, B 为多项式

A = 3X^2 + 5X^4 + 3 + 4X; B = 7X^7 + 2X + 3X^4

A, B运算后系数为0

A = 2X^2; B = -2X^2

A,B其中不全存在

A = ; B = 2X^2 + 3X^3 + 2

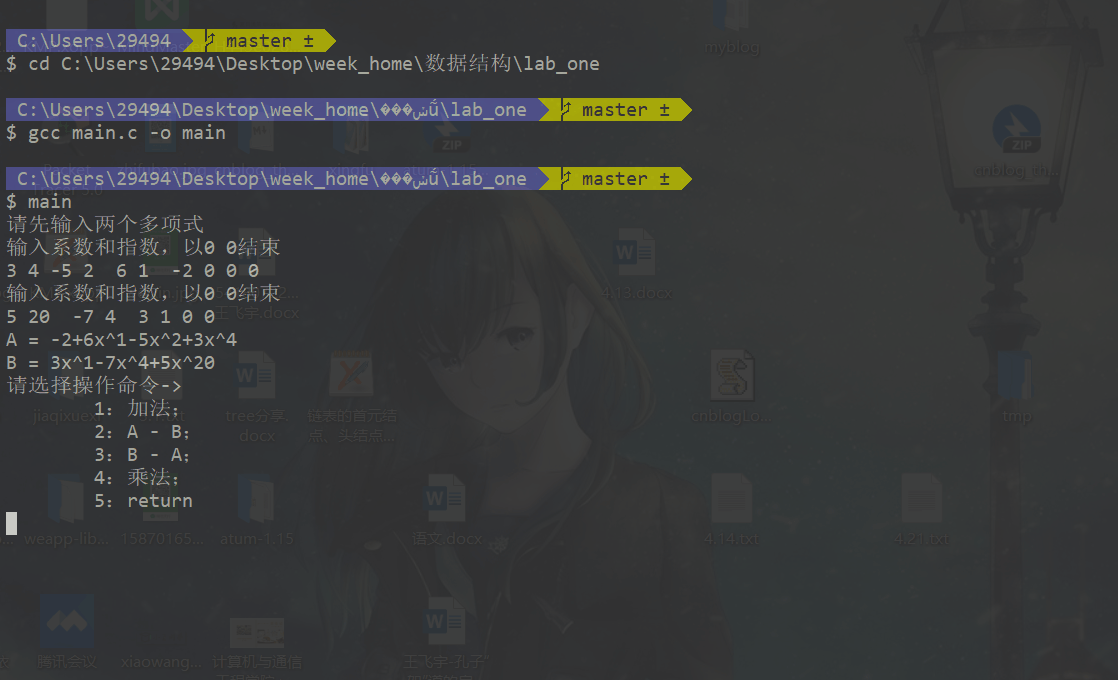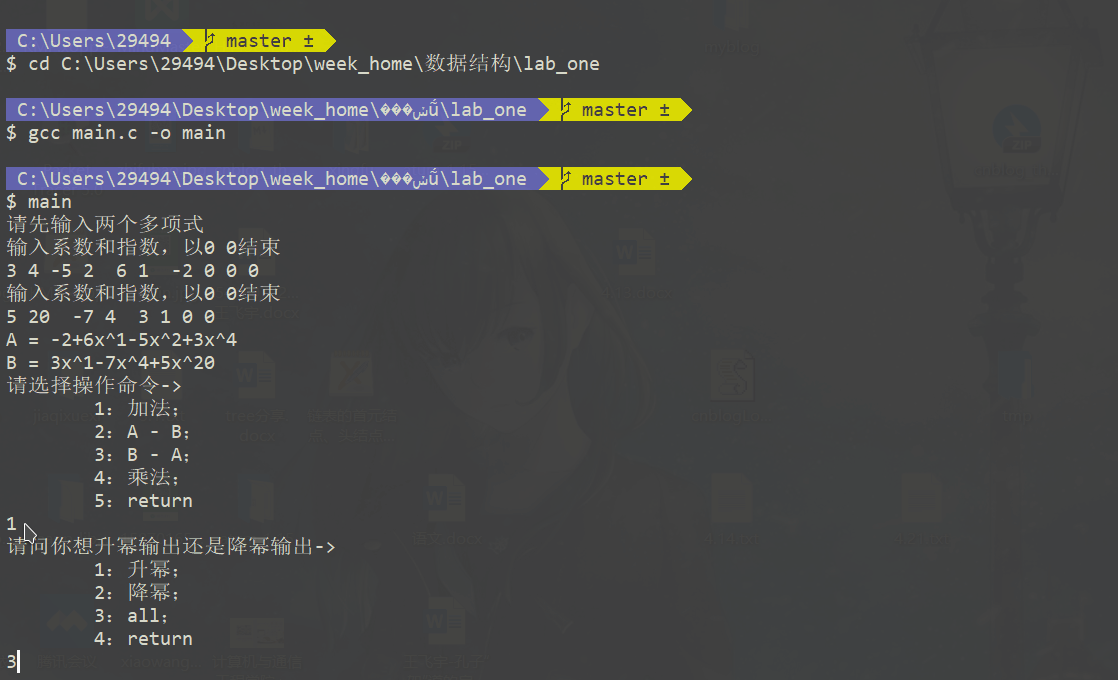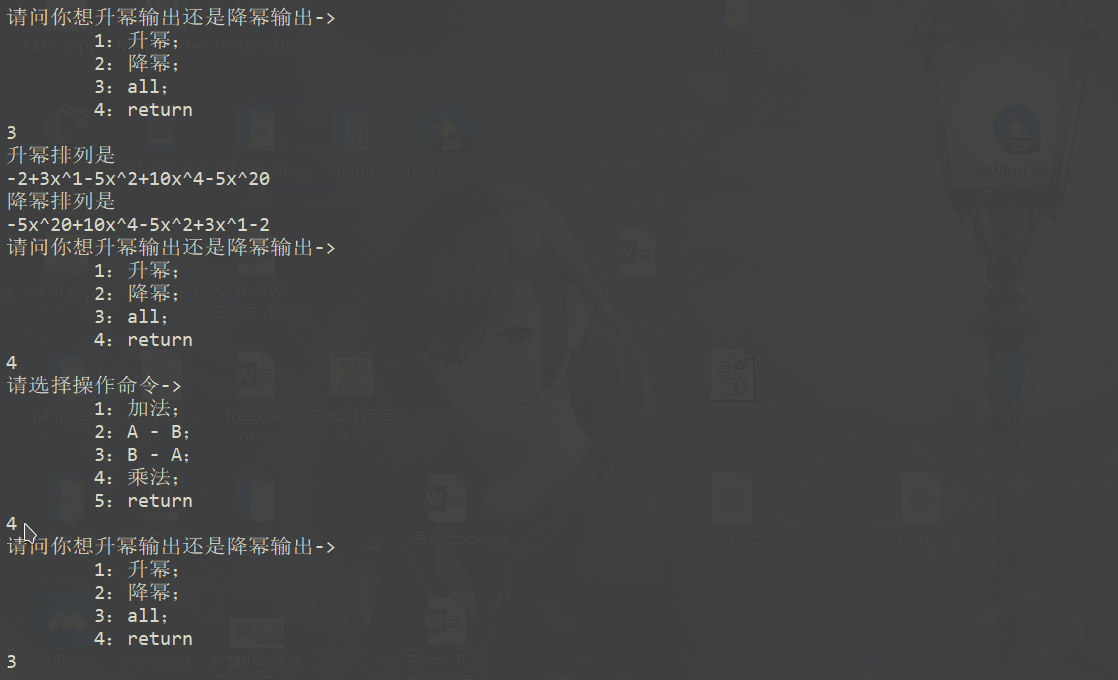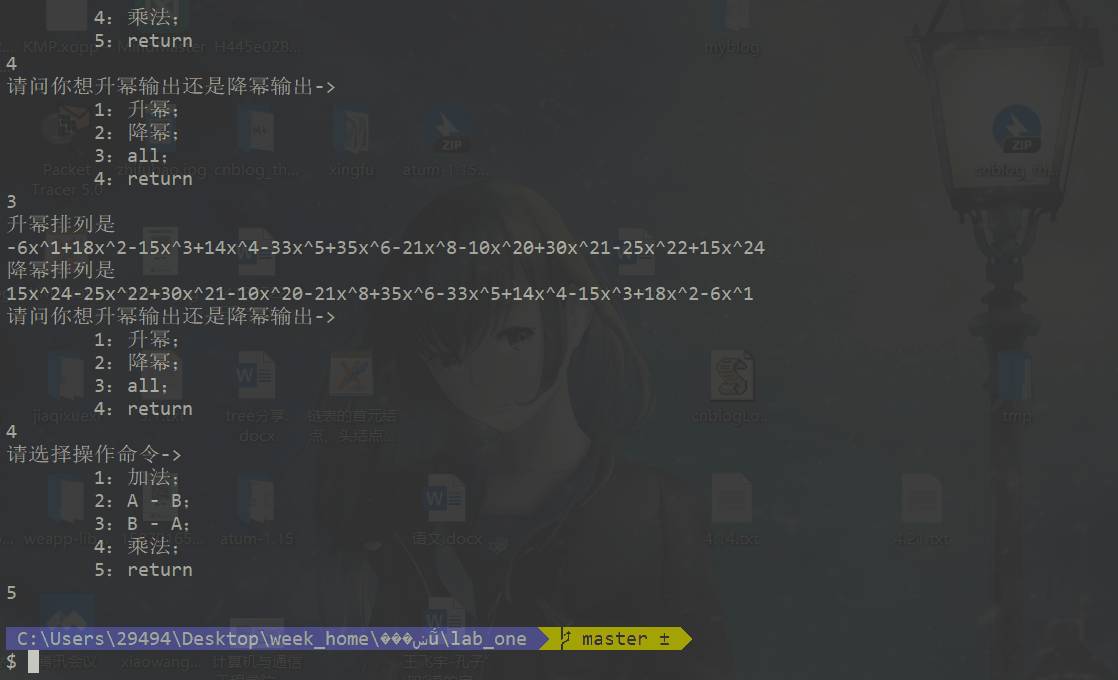
综合方案

A = 3X^4-5X^2+6X^1-2X^0

B = 5X^20-7X^4+3^1

完整代码

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef struct node * LIST;
struct node
{
    int c;//系数
    int n;//指数
    LIST NEXT;
};
LIST input();
void insert(int c, int n, LIST head);//插入和维护升幂
void add(LIST A, LIST B);//A链节点和B链节点直接insert里面丢，进去就有序
void output(LIST head);//
LIST reversed(LIST head);//反转->降幂
void sub(LIST A, LIST B);//A链节点和B链负节点直接insert里面丢，进去就有序
void mul(LIST A, LIST B);//A链节点 * B链节点(for for)直接insert(c*c, n+n, head)里面丢，进去就有序
void uptate(LIST head);//A链节点B链节点删除c=0节点
void show(LIST head);//展示\t,switch,
void init();//初始化
int main(int argc, char const *argv[])
{
    init();
    return 0;
}
void init()//初始化
{
    printf("请先输入两个多项式\n");
    LIST A = input();
    LIST B = input();
    printf("A = ");output(A);
    printf("B = ");output(B);
    while(1){
        int flag;
        printf("请选择操作命令-> \n \t1：加法；\n\t2：A - B；\n\t3：B - A；\n\t4：乘法；\n\t5：return\n");
        scanf("%d", &flag);
        switch (flag){
            case 1:
                add(A, B);
                break;
            case 2:
                sub(A, B);
                break;
            case 3:
                sub(B, A);
                break;
            case 4:
                mul(A, B);
                break;
            case 5:
                return;
        }
    }
}
void insert(int c, int n, LIST head)
{
    //头结点性质
    LIST tmp = (LIST)malloc(sizeof(struct node));
    tmp->n = n, tmp->c = c, tmp->NEXT = NULL;
    LIST P = head;
    while(P->NEXT)
    {
        //相等
        if(P->NEXT->n == tmp->n)
        {
            P->NEXT->c += tmp->c;
            return;
        }
        if(P->NEXT->n > tmp->n)
            break;
        P = P->NEXT;
    }
    //找到最后还没有找到
    if(!P->NEXT)
    {
        P->NEXT = tmp;
        return;
    }
    tmp->NEXT = P->NEXT;
    P->NEXT = tmp;
}
LIST input()
{
    printf("输入系数和指数，以0 0结束\n");
    //输入系数和指数
    LIST head = (LIST)malloc(sizeof(struct node));
    head->NEXT = NULL;
    int n, c;
    while(scanf("%d%d", &c, &n), n || c)
        insert(c, n, head);
    return head;
}
void add(LIST A, LIST B)
{
    LIST head = (LIST)malloc(sizeof(struct node));
    head->NEXT = NULL;
    LIST P = A->NEXT;
    while(P)
        insert(P->c, P->n, head), P = P->NEXT;
    P = B->NEXT;
    while(P)
        insert(P->c, P->n, head), P = P->NEXT;
    uptate(head);
    show(head);
}
void sub(LIST A, LIST B)
{
    LIST head = (LIST)malloc(sizeof(struct node));
    head->NEXT = NULL;
    LIST P = A->NEXT;
    while(P)
        insert(P->c, P->n, head), P = P->NEXT;
    P = B->NEXT;
    while(P)
        insert(-P->c, P->n, head), P = P->NEXT;
    uptate(head);
    show(head);
}
void mul(LIST A, LIST B)
{
    LIST head = (LIST)malloc(sizeof(struct node));
    head->NEXT = NULL;
    LIST i = A->NEXT;
    //if A NULL
    LIST j = B->NEXT;
    if(!i)
    {
        while(j)
        {
            insert(j->c, j->n, head);
            j = j->NEXT;
        }
        uptate(head);
        show(head);
        return;
    }
    //if B NULL
    if(!j)
    {
        while(i)
        {
            insert(i->c, i->n, head);
            i = i->NEXT;
        }
        uptate(head);
        show(head);
        return;
    }
    while(i){
        j = B->NEXT;
        while(j)
        {
            insert(i->c * j->c, i->n + j->n, head);
            j = j->NEXT;
        }
        i = i->NEXT;
    }
    uptate(head);
    show(head);
}
void uptate(LIST head)
{
    LIST P = head;
    while(P->NEXT)
    {
        if(P->NEXT->c == 0){
            P->NEXT = P->NEXT->NEXT;
            continue;
        }
        P = P->NEXT;
    }
}
void output(LIST head)
{
    LIST P = head->NEXT;
    if(!P) return;
    //输出第一个
    if(P->c < 0)
        printf("-");
    if(P->n == 0)
        printf("%d", abs(P->c));
    else
        printf("%dx^%d", abs(P->c), P->n);
    P = P->NEXT;
    //继续输出
    while(P)
    {
        if(P->n == 0)
            printf("%c%d", P->c > 0 ? ‘+‘ : ‘-‘,abs(P->c));
        else
            printf("%c%dx^%d", P->c > 0 ? ‘+‘ : ‘-‘, abs(P->c), P->n);
        P = P->NEXT;
    }
    printf("\n");
}
LIST reversed(LIST head)
{
    LIST rear, P = head->NEXT;
    rear = (LIST)malloc(sizeof(struct node));
    rear->NEXT = NULL;
    while(P)
    {
        LIST tmp = (LIST)malloc(sizeof(struct node));
        tmp->NEXT = NULL, tmp->c = P->c, tmp->n = P->n;
        tmp->NEXT = rear->NEXT;
        rear->NEXT = tmp;
        P = P->NEXT;
    }
    return rear;
}
void show(LIST head)
{
    while(1){
        int flag;
        printf("请问你想升幂输出还是降幂输出-> \n\t1：升幂；\n\t2：降幂；\n\t3：all；\n\t4：return\n");
        scanf("%d", &flag);
        switch (flag){
            case 1:
                printf("升幂排列是\n");
                output(head);
                break;
            case 2:
                printf("降幂排列是\n");
                output(reversed(head));
                break;
            case 3:
                printf("升幂排列是\n");
                output(head);
                printf("降幂排列是\n");
                output(reversed(head));
                break;
            case 4:
                return;
        }
    }
}

多项式运算

标签：情况 style typedef 拓展 tps 问题 radius family height

原文地址：https://www.cnblogs.com/wfybeliefs/p/12748405.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行