标签:矩形 算法分析 mat 整数 net 中间 记录 inf map
水平不足以做出这题 学习这题 原文转自如下
https://blog.csdn.net/weixin_43845956/article/details/104318097
题目描述
あなたの蛙は旅立っています!
你的蛙正在考虑它应该按怎样的路线去旅行。这些景点可以抽象为 N 个镶嵌着的六边形。每个景点 i 都有一个快乐度 Hi 。蛙蛙想要决定一条路线,使得路线上的景点快乐度之和最大。而你的蛙蛙又是一只不走回头路的蛙,所以它每次只能朝远处走。
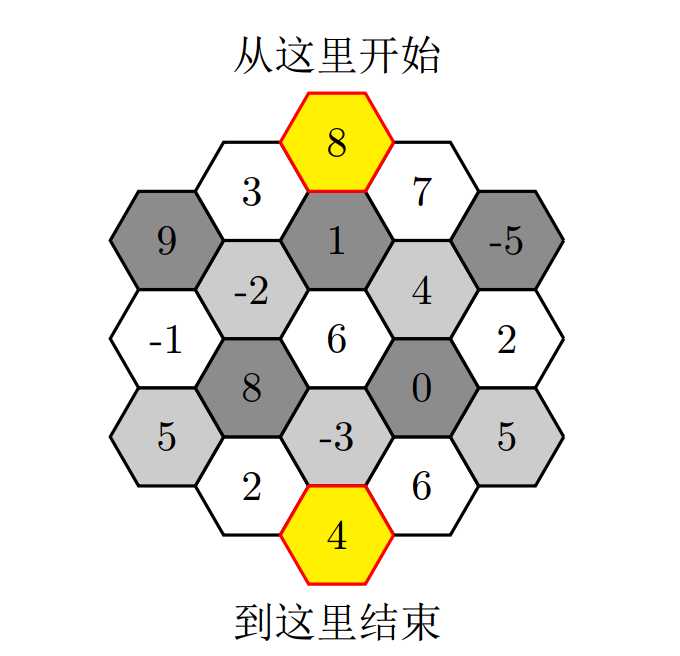
比如,上图就是一个例子。蛙蛙会从最上方的黄色六边形出发,每次只能走到下方的直接相邻的三个六边形中(边界上可能只有一个或两个直接相邻的六边形),这样一直走到最下方的黄色六边形中。这一段旅程总的快乐值定义为途径的景点的快乐值之和。蛙蛙想要找到一条快乐值最大的路径开始它的旅行。
你的蛙蛙已经迫不及待了,赶紧 したく 然后 かんりょう 吧!
输入描述
输入第一行一个数 N , 表示大六边形的边长(边长定义为大六边形的一条边上小六边形的个数)。
接下去 4N - 3 行,每行 1 ∼ N 个整数 Hi ,描述大六边形中的一行景点的快乐度。具体可以看题目描述中的图。图中,颜色相同的并且在同一行的数字将会作为输入中的一行。
输出描述
输出共一行,一个整数,表示最大能得到的快乐值。
输入
3
8
3 7
9 1 -5
-2 4
-1 6 2
8 0
5 -3 5
2 6
4
输出
45
说明
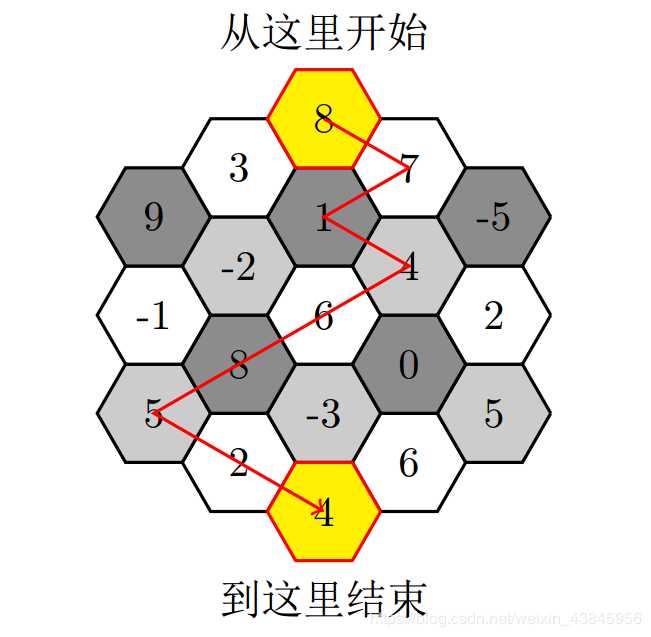
备注
2 ≤ N ≤ 800
?0 ≤ |Hi| ≤2000
算法分析
1、找出输入规律,将输入的数据,存在二维数组中
将输入分为三段:
第一段:
1 ~ N 行,分别为 1 ~ N 个数据输入
第二段:
N ~ 3N - 3 行
第 N 行为 N - 1 个数据,第 N + 1 行为 N 个数据,第 N + 2 行为 N - 1 个数据 …依此类推
第三段:
3N - 3 ~ 4N - 3 行,分别为 N ~ 1 个数据输入
2、压缩大六边形,为二维矩形形状
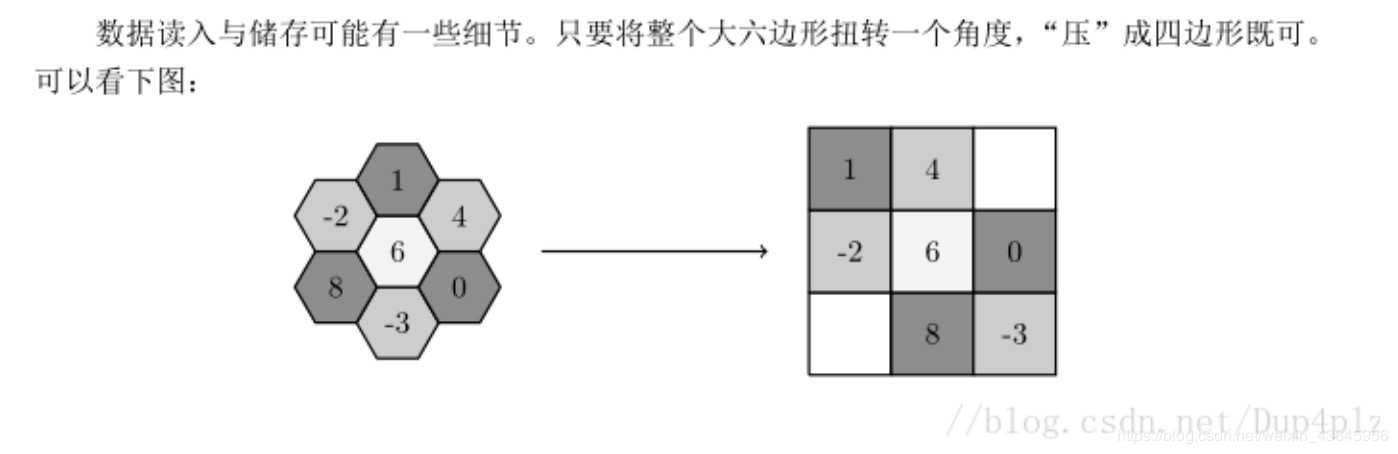

3、列出dp状态方程对二维数组进行计算
状态方程为 dp[i][j] = max(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + map[i][j];
特殊处理:
在dp之前对于,对于0行n列的数据 和 n行0列的数据,单独处理。
因为如果单纯使用dp状态方程去求解,那么就会出现特殊情况,单独处理之后,dp状态方程的情况就变得单一了。
解题代码
#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn = 3e3 + 5;
int Map[maxn][maxn]; //存放压缩存储后的数据
int Cur[maxn]; //存放每行应该输入的数据的个数
int dp[maxn][maxn]; //dp方程求解
int main()
{
int n;
scanf("%d", &n);
memset(Map, 0xc0, sizeof(Map)); //初始化为负无穷,使得后续无效dp不影响结果
memset(Cur, 0, sizeof(Cur));
memset(dp, 0, sizeof(dp));
int vis = 1 + (4 * (n - 1)); //输入的行数
int cur = 2 * n - 1; //旋转之后的压缩矩阵的大小
//计算每一行存多少个数
//上三行输入的数目 由1~n
int i, j;
for (i = 0; i < n; i++)
Cur[i] = i + 1;
//上三行输入的数目 由1~n
//中间三行,如果n为奇数,则第一行为n个,如果n为偶数,则第一行为n-1个
int opt[2];
opt[0] = n - 1; //第一次输入就为n-1个数据
opt[1] = n; //第二次输入就为n个数据
int flag = 0;
for ( ; i < (vis - n); i++, flag = !flag) //i < 3n - 3
Cur[i] = opt[flag];
//中间三行,如果n为奇数,则第一行为n个,如果n为偶数,则第一行为n-1个
//上三行输入的数目 由n~1
for (j = n ; i < vis; i++, j--)
Cur[i] = j;
//上三行输入的数目 由n~1
//计算每一行存多少个数
//输入
vector <int> v[vis];
int temp;
for (i = 0; i < vis; i++)
{
for (j = 0; j < Cur[i]; j++)
{
scanf("%d", &temp);
v[i].push_back(temp);
}
}
//输入
int len = cur/2 + 1; //将数组分两部分进行处理
//上半部分,列始终都是从0开始,列数随行数+1而+1
flag = 0;
for (i = 0, j = n; i < len; i++, j++) //j按照规律下一层比上一层多一个数
{
for (int l = 0, k = flag; l < j; l++, k++) //每次从未存完的最底层开始从尾部弹出数存入数组
{
Map[i][l] = v[k][v[k].size() - 1];
v[k].pop_back();
if (v[k].size() == 0) //记录从0 - (4n-3)中未存完的最低层
flag++;
}
}
//上半部分,列始终都是从0开始,列数随行数+1而+1
//下半部分,列从1开始,随着行数+1,列向后偏移1位
for (j -= 2; i < cur; i++, j--) //j = 2*n + 1/2 , 也可以写成j从1~n的增加,
{
for (int l = (cur - j), k = flag; l < cur; l++, k++) //l用来标志从哪一列开始存
{
Map[i][l] = v[k][v[k].size() - 1];
v[k].pop_back();
if (v[k].size() == 0)
flag++;
}
}
//下半部分,列从1开始,随着行数+1,列向后偏移1位
//提前对0行和0列进行初始化,使得dp的方程普遍化
dp[0][0] = Map[0][0];
for (i = 1; i < cur; i++)
{
dp[0][i] = dp[0][i - 1] + Map[0][i];
dp[i][0] = dp[i - 1][0] + Map[i][0];
}
//提前对0行和0列进行初始化,使得dp的方程普遍化
//dp方程
for (i = 1; i < cur; i++)
{
for (j = 1; j < cur; j++)
dp[i][j] = max(max(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + Map[i][j];
}
//dp方程
cout << dp[cur - 1][cur - 1] << endl;
}
总结一下 有几个小点
标签:矩形 算法分析 mat 整数 net 中间 记录 inf map
原文地址:https://www.cnblogs.com/luolinjin/p/12773549.html